Bài 1: Tìm x ở hình 5,6
Giải:
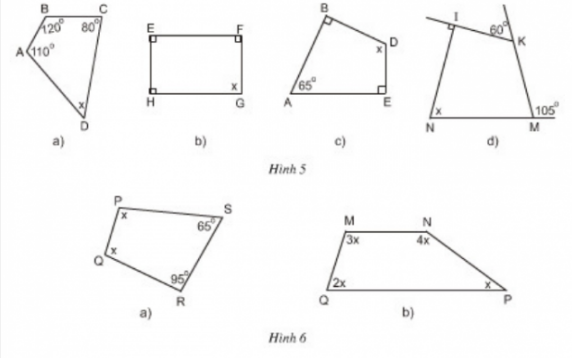
Ở hình 5:
a) x = 3600 – ( 1100 + 1200 + 800) = 500
b) x = 3600 – ( 900 + 900 + 900) = 900
c) x = 3600 – ( 900 + 900 + 650) = 1150
d) x = 3600 – ( 750 + 1200 + 900) = 750
Vì \[\widehat{K}\] = 1800 – 600 = 1200
\[\widehat{M}\]= 1800 – 1050 = 750
Ở hình 6:
a) 2x = 3600 – (650 + 950)
\[\Rightarrow \] x = 1000
b) 2x + 3x + 4x + x = 3600
10x = 3600 \[\Rightarrow \] x = 360
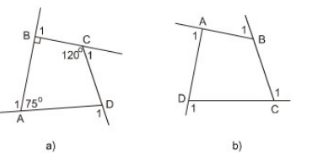
Bài 2: Góc kề bù với một góc của tứ giác gọi là góc ngoài của tứ giác:
a) Tính các góc ngoài của tứ giác ở hình a
b) Tính tổng các góc ngoài của tứ giác ở hình b ( tại mỗi đỉnh của tứ giác chỉ chọn một góc ngoài): \[\widehat{{{A}_{1}}}+\widehat{{{B}_{1}}}+\widehat{{{C}_{1}}}+\widehat{{{D}_{1}}}\]= ?
c) Có nhận xét gì về tổng các góc ngoài của tứ giác?
Giải:
a) Góc ngoài còn lại: \[\widehat{D}\] = 3600 – ( 750 + 900 + 1200) = 750
Ta tính được các góc ngoài tại các đỉnh A, B, C, D lần lượt là: 1050, 900, 600, 1050
b) Hình b:
Tổng các góc trong \[\widehat{{{A}_{1}}}+\widehat{{{B}_{1}}}+\widehat{{{C}_{1}}}+\widehat{{{D}_{1}}}\]= 3600
Nên tổng các góc ngoài:
\[\widehat{{{A}_{1}}}+\widehat{{{B}_{1}}}+\widehat{{{C}_{1}}}+\widehat{{{D}_{1}}}\]= ( 1800 -\[\widehat{{{A}_{1}}}\]) + (\[{{180}^{0}}-\widehat{{{B}_{1}}}\]) + ( 1800 - \[\widehat{{{C}_{1}}}\]) + ( 1800 - \[\widehat{{{D}_{1}}}\])
= ( 1800.4 – ( \[\widehat{{{A}_{1}}}+\widehat{{{B}_{1}}}+\widehat{{{C}_{1}}}+\widehat{{{D}_{1}}}\])) = 7200 – 3600 = 3600
c) Nhận xét: Tổng các góc ngoài của tứ giác bằng 3600
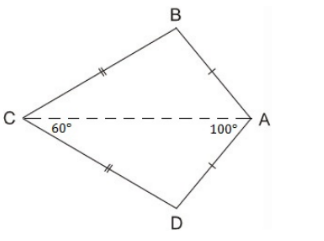
Bài 3: Ta gọi tứ giác ABCD trên hình có AB = AD, CB = CD là hình “cái diều”
a) Chứng minh rằng AC là đường trung trực của BD
b) Tính \[\widehat{B}\]; \[\widehat{D}\] biết rằng \[\widehat{A}\]=1000; \[\widehat{C}\]=600
Giải:
a) Ta có AB = AD (gt) \[\Rightarrow \] A thuộc đường trung trực của BD
CB = CD (gt) \[\Rightarrow \] C thuộc đường trung trực của BD
Vậy AC là đường trung trực của BD
b) Xét \[\Delta ABC\] và \[\Delta ADC\] có
AB = AD (gt)
BC = DC (gt)
AC: cạnh chung
Nên \[\Delta ABC\]=\[\Delta ADC\](c.c.c)
Suy ra \[\widehat{B}\]=\[\widehat{D}\]
Ta có: \[\widehat{B}\]+\[\widehat{D}\]=3600 – ( 1000 + 600) = 2000
Do đó \[\widehat{B}\]=\[\widehat{D}\]= 1000







