Đường Tiệm Cận

ĐƯỜNG TIỆM CẬN CỦA HÀM SỐ

A/Lý thuyết

1/Tiệm cận ngang

Đường thẳng $y={{y}_{0}}$ được gọi là tiệm cận ngang của đồ thị hàm số $y=f(x)$ nếu $\underset{x\to +\infty }{\mathop{\lim }}\,f(x)={{y}_{0}}$ hoặc $\underset{x\to -\infty }{\mathop{\lim }}\,f(x)={{y}_{0}}$

2/Tiệm cận đứng

Đường thẳng $x={{x}_{0}}$ được gọi là tiệm cận đứng của đồ thị hàm số $y=f(x)$ nếu tồn tại ít nhất một trong các điều kiện:

$\underset{x\to x_{0}^{-}}{\mathop{\lim }}\,=+\infty$ ;$\underset{x\to x_{0}^{+}}{\mathop{\lim }}\,=+\infty$

$\underset{x\to x_{0}^{-}}{\mathop{\lim }}\,=-\infty$ ;$\underset{x\to x_{0}^{+}}{\mathop{\lim }}\,=-\infty$

3/Tiệm cận xiên

Đường thẳng $y=ax+b$ được gọi là tiệm cận xiên của hàm số $y=f(x)$ nếu $\underset{x\to +\infty }{\mathop{\lim }}\,\left[ f(x)-\left( ax+b \right) \right]=0$ hoặc $\underset{x\to -\infty }{\mathop{\lim }}\,\left[ f(x)-\left( ax+b \right) \right]=0$

Để tính nhanh a, b ta áp dụng các công thức sau:

$a=\underset{x\to +\infty }{\mathop{\lim }}\,\frac{f(x)}{x};b=\underset{x\to +\infty }{\mathop{\lim }}\,\left[ f(x)-ax \right]$

Hoặc $a=\underset{x\to -\infty }{\mathop{\lim }}\,\frac{f(x)}{x};b=\underset{x\to -\infty }{\mathop{\lim }}\,\left[ f(x)-ax \right]$

(Nếu a=0 thì ta có tiệm cận ngang)

*QUY TẮC TÌM CÁC ĐƯỜNG TIỆM CẬN

+ Tìm tiệm cận ngang và tiệm cận đứng

-$\underset{x\to \pm \infty }{\mathop{\lim }}\,f(x)=>TCN$

-$\underset{x\to x_{0}^{\pm }}{\mathop{\lim }}\,f(x)=>TC\text{D}$

Lưu ý: ${{x}_{0}}$ thương là một nghiệm của mẫu

+ Tìm tiệm cận xiên

-C1: Viết lại hàm số dưới dạng $y=ax+b+g(x)$

$\underset{x\to \pm \infty }{\mathop{\lim }}\,\left[ y-\left( ax+b \right) \right]=0=>TCX$

-C2: Tính $a=\underset{x\to \pm \infty }{\mathop{\lim }}\,\frac{f(x)}{x}$và $b=\underset{x\to \infty }{\mathop{\lim }}\,\left[ f(x)-ax \right]$ => TCX

B/Ví dụ

VD1: Tìm tiệm cận ngang và tiệm cận đứng của đồ thị hàm số $y=\frac{2x-1}{x+2}$

Tập xác định: $(-\infty ;-2)\cup (-2;+\infty )$

$\underset{x\to \pm \infty }{\mathop{\lim }}\,\frac{2x-1}{x+2}=2$ => $y=2$ là tiệm cận ngang của đồ thị hàm số đã cho

$\underset{x\to {{(-2)}^{+}}}{\mathop{\lim }}\,\frac{2x-1}{x+2}=-\infty$ ;

\[\underset{x\to {{(-2)}^{-}}}{\mathop{\lim }}\,\frac{2x-1}{x+2}=+\infty\]

=> $x=-2$ là tiệm cận đứng của đồ thị hàm số đã cho

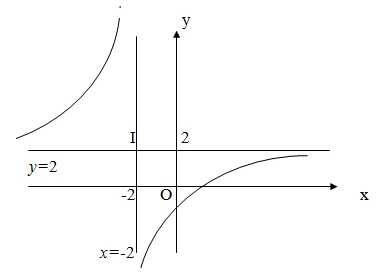
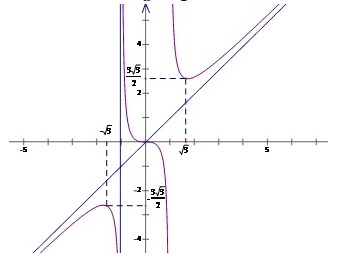
VD2: Tìm tiệm cận xiên của đồ thị hàm số $y=f(x)=x+\frac{x}{{{x}^{2}}-1}$

Ta có $\underset{x\to \infty }{\mathop{\lim }}\,\left[ f(x)-x \right]=\underset{x\to \infty }{\mathop{\lim }}\,\frac{x}{{{x}^{2}}-1}=0$ => $y=x$ là tiệm cận xiên của đồ thị hàm số đã cho

C/ Bài tập tự luyện

Câu 1: Tìm các đường tiệm cận ngang và tiệm cận xiên của đồ thị hàm số $y=\frac{2x+3}{x-4}$

A. $x=4;y=\frac{1}{2}$

B.$x=-4;y=\frac{1}{2}$

C.$x=4;y=2$

D.$x=4;y=-\frac{3}{2}$

Câu 2: Số các đường tiệm cận của đồ thị hàm số $y=\frac{{{x}^{2}}-3x+2}{x-3}$

A.0

B.1

C.2

D.3

Câu 3: Tìm tất cả các đường tiệm cận của đồ thị hàm số $y=\frac{3x-2}{1-x}$

A.$x=1;y=3$

B.$x=1;y=-3$

C.$x=3;y=1$

D.$x=-3;y=1$

Câu 4: Số đường tiệm cận của đồ thị hàm số $y={{x}^{3}}-3{{x}^{2}}+4x-11$

A.1

B.0

C.3

D.4

Câu 5: Đường thẳng $y=c$ có bao nhiêu đường tiệm cận

A.1

B.3

C.2

D.0

Câu 5: Cho hàm số $y=\frac{m{{x}^{2}}+({{m}^{2}}+m+2)x+{{m}^{3}}+3}{x+1}$ . Tìm m để khoảng cách từ gốc tọa độ đến tiệm cận xiên hoặc ngang là nhỏ nhất

A.0

B.1

C.2

D.-1

Câu 6: Cho hàm số $y=\frac{x-1}{x-2}$ . Tìm điểm M thuộc đồ thì hàm số sao cho tổng khoảng cách từ M đến hai đường tiệm cạn đạt giá trị nhỏ nhất

A.M(0;0)

B.M(3;2) hoặc M(1;0)

C.M(2;1)

C.Không tìm được

Câu 7: Cho hàm số $y=\frac{{{x}^{2}}+2mx+3}{x+m}$ . Tìm m để đồ thị hàm số có tiệm xiên đi qua điểm A(-1;0)

A.0

B.1

C.-1

D.2

Câu 8: Tìm tất cả các giá trị thực của tham số m sao cho đồ thị hàm số $y=\frac{x+1}{\sqrt{m{{x}^{2}}+1}}$ có hai tiệm cận ngang

A.m < 0

B.m = 0

C.m > 0

D.Không tồn tại giá trị m

Câu 9: Đồ thị hàm số nào sau đây có đường tiệm cận

A.$y={{x}^{3}}+2{{x}^{2}}+4$

B.$y={{x}^{4}}+{{x}^{2}}+1$

C.$y=-{{x}^{3}}+2x-11$

D.\[y=\frac{1}{x}\]

Câu 10: Cho hàm số $y=\frac{a{{x}^{2}}+3ax+2a+1}{x+2}$ có đồ thị (C). Với mị a, tiệm cận của (C) luôn đi qua một điểm cố định. Tọa độ điểm cố định đó là

A.(-1;2)

B.(1;-2)

C.(-1;0)

D.(1;0)

ĐÁP ÁN