Câu 1: Cho một chất điểm dao động điều hòa với biên độ A, tốc độ cực đại là V. Khi tốc độ \[v=\frac{1}{2}V\] thì li độ x được tính bằng biểu thức
A.\[x=\pm \sqrt{\frac{3}{2}}A\] B.\[x=\pm \frac{\sqrt{2}}{2}A\] C.\[x=\pm \frac{\sqrt{3}}{2}A\] D.\[x=\pm \frac{\sqrt{3}}{2}A\]
Hướng dẫn
Ta có: \[{{\left( \frac{x}{A} \right)}^{2}}+{{\left( \frac{v}{A\omega } \right)}^{2}}=1\Leftrightarrow {{\left( \frac{x}{A} \right)}^{2}}+{{\left( \frac{\frac{1}{2}v}{V} \right)}^{2}}=1\Rightarrow {{\left( \frac{x}{A} \right)}^{2}}=\frac{3}{4}\to x=\pm \frac{\sqrt{3}}{2}A\]
Chọn đáp án C
Câu 2: Cho một chất điểm dao động điều hòa với biên độ A, gia tốc cực đại là \[{{a}_{m}}\] . Tại một thời điểm, li độ là x và gia tốc là a. Kết luận nào sau đây là không đúng.
A. Khi \[x=\pm \frac{1}{2}A\] thì \[a=\mp \frac{1}{2}{{a}_{m}}\]
B. Khi \[x=\pm \frac{\sqrt{2}}{2}A\] thì \[a=\mp \frac{\sqrt{2}}{2}{{a}_{m}}\]
C. Khi \[a=\mp \frac{\sqrt{3}}{2}{{a}_{m}}\] thì \[x=\pm \frac{\sqrt{3}}{2}A\]
D. Khi \[x=\pm A\] thì a=0
Hướng dẫn
Ta có x và A dao động ngược pha nhau nên trong 4 đáp án đáp án sai là \[x=\pm A\] thì a=0
Chọn đáp án D
Câu 3: Cho một chất điểm dao động điều hòa với biên độ 10 cm, tốc độ cực đại là 20 cm/s. Khi li độ là 5 cm thì vận tốc bằng
A.\[\pm 10\sqrt{3}cm/s\] B.\[\pm 10cm/s\] C. 10 cm / s D.\[10\sqrt{3}cm/s\]
Hướng dẫn
Ta có: \[{{\left( \frac{x}{A} \right)}^{2}}+{{\left( \frac{v}{A\omega } \right)}^{2}}=1\Leftrightarrow v=\pm 10\sqrt{3}cm/s\]
Chọn đáp án A
Câu 4: Cho một chất điểm dao động điều hòa với biên độ 20 cm, tốc độ cực đại là \[10\sqrt{2}cm/s\]. Khi vận tốc là 10 cm/s thì li độ bằng
A.\[10\sqrt{2}cm\] B.\[\pm 10cm\] C.\[\pm 10\sqrt{2}cm\] D.10cm
Hướng dẫn
Ta có: \[{{\left( \frac{x}{A} \right)}^{2}}+{{\left( \frac{v}{A\omega } \right)}^{2}}=1\Leftrightarrow x=\pm 10\sqrt{2}cm\]
Chọn đáp án C
Câu 5: Cho một chất điểm dao động điều hòa với biên độ 10 cm, tốc độ cực đại là 30 cm/s. Khi vận tốc là 15 cm/s thì li độ bằng
A.\[5\sqrt{3}cm\] B.\[\pm 5\sqrt{3}cm\] C. -5 cm D. 5 cm
Hướng dẫn
Ta có: \[{{\left( \frac{x}{A} \right)}^{2}}+{{\left( \frac{v}{A\omega } \right)}^{2}}=1\Leftrightarrow x=\pm 5\sqrt{3}cm\]
Chọn đáp án B
Câu 6: Cho một chất điểm dao động điều hòa với biên độ 10 cm, gia tốc cực đại là \[8m/{{s}^{2}}\] . Khi gia tốc là \[-4m/{{s}^{2}}\] thì li độ bằng
A. - 5 cm B. 5 cm C. \[5\sqrt{3}cm\] D. \[\pm 5\sqrt{3}cm\]
Hướng dẫn
Ta có: \[{{a}_{\max }}={{\omega }^{2}}A\to {{\omega }^{2}}=80\]
\[\Rightarrow \]\[a=-{{\omega }^{2}}x\to x=5cm\]
Chọn đáp án B
Câu 7 : Cho một chất điểm dao động điều hòa với biên độ 10 cm, gia tốc cực đại là \[8m/{{s}^{2}}\] . Khi gia tốc là \[4\sqrt{3}m/{{s}^{2}}\] thì li độ bằng
A. -5 cm B. 5 cm C.\[-5\sqrt{3}cm\] D.\[5\sqrt{3}cm\]
Hướng dẫn
Ta có: \[{{a}_{\max }}={{\omega }^{2}}A\to {{\omega }^{2}}=80\]
\[\Rightarrow a=-{{\omega }^{2}}x\to x=-5\sqrt{3}cm\]
Chọn đáp án C
Câu 8: Cho một chất điểm dao động điều hòa với tần số góc \[\omega \] và biên độ A. Gọi x là li độ; v là tốc độ tức thời. Biểu thức nào sau đây là đúng.
A.\[A=v+\frac{x}{\omega }\]
B.\[A=x+\frac{v}{\omega }\]
C.\[{{A}^{2}}={{v}^{2}}+{{\left( \frac{x}{\omega } \right)}^{2}}\]
D.\[{{A}^{2}}={{x}^{2}}+{{\left( \frac{v}{\omega } \right)}^{2}}\]
Hướng dẫn
Chất điểm dao động điều hòa với tần số góc \[\omega \] và biên độ A . Gọi x là li độ; v là tốc độ tức thời . Ta có: \[{{A}^{2}}={{x}^{2}}+{{\left( \frac{v}{\omega } \right)}^{2}}\]
Chọn đáp án D
Câu 9: Cho một chất điểm dao động điều hòa với tần số góc \[\omega \]. Gọi v là tốc độ tức thời; a là gia tốc tức thời; V tốc độ cực đại. Biểu thức nào sau đây là đúng.
A.\[\left( V-v \right)\omega =a\]
B.\[\left( {{V}^{2}}-{{v}^{2}} \right){{\omega }^{2}}={{a}^{2}}\]
C.\[\left( {{V}^{2}}+{{v}^{2}} \right){{\omega }^{2}}={{a}^{2}}\]
D. \[(V+v)\omega =A\]
Hướng dẫn
Chất điểm dao động điều hòa với tần số góc \[\omega \] và biên độ A. Gọi v là tốc độ tức thời; a là gia tốc tức thời; V tốc độ cực đại
Ta có: \[{{V}^{2}}={{v}^{2}}+{{\left( \frac{a}{\omega } \right)}^{2}}\to \]\[\left( {{V}^{2}}-{{v}^{2}} \right){{\omega }^{2}}={{a}^{2}}\]
Chọn đáp án B
Câu 10: Cho một chất điểm dao động điều hòa với tần số góc 10 rad/s và biên độ A. Khi li độ là 3 cm thì vận tốc là 40 cm/s. Biên độ A bằng.
A. 5 cm B. 25 cm C. 10 cm D. 50 cm
Hướng dẫn
Ta có: \[{{A}^{2}}={{x}^{2}}+{{\left( \frac{v}{\omega } \right)}^{2}}=25\to A=5cm\]
Chọn đáp án A
Câu 11: Li độ và tốc độ của một vật động điều hòa liên hệ với nhau theo biểu thức \[{{10}^{3}}{{x}^{2}}={{10}^{5}}-{{v}^{2}}\].Trong đó x và v lần lượt tính theo đơn vị cm và cm/s. Lấy \[{{\pi }^{2}}=10\]. Khi gia tốc của vật là \[50m/{{s}^{2}}\] thì tốc độ của vật là
A.\[50\pi cm/s\]
B.\[50\pi \sqrt{3}cm/s\]
C.0
D.\[100\pi cm/s\]
Hướng dẫn
Lấy đạo hàm 2 về ta có: \[{{10}^{3}}{{x}^{2}}={{10}^{5}}-{{v}^{2}}\to x=\frac{-a}{{{10}^{3}}}=-5cm\]
Thay vào biểu thức => v=\[50\pi \sqrt{3}cm/s\]
Chọn đáp án B
Câu 12: Một vật dao động điều hoà với phương trình liên hệ v, x dạng \[\frac{{{x}^{2}}}{48}+\frac{{{v}^{2}}}{0,768}=1\] , trong đó x (cm), v (m/s). Lấy \[{{\pi }^{2}}=10\].Tại t = 0 vật qua li độ \[-2\sqrt{3}cm\] và đang đi về VTCB. Phương trình dao động của vật là
A.\[x=4\cos \left( 4\pi t+\frac{\pi }{6} \right)cm\]
B.\[x=4\sqrt{3}\cos \left( 4\pi t+\frac{\pi }{6} \right)cm\]
C.\[x=4\sqrt{2}\cos \left( 4\pi t+\frac{\pi }{6} \right)cm\]
D.\[x=4\sqrt{3}\cos \left( 4\pi t-\frac{2\pi }{3} \right)cm\]
Hướng dẫn
Phương trình tổng quát cần tìm \[x=A\cos \left( \omega t+\varphi \right)\]
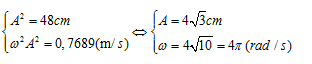
Gốc thời gian t=0; vật qua vị trí x=\[-2\sqrt{3}cm\] hay \[-\frac{A}{2}(+)\to \varphi =-\frac{2\pi }{3}rad\]
Vậy phương trình dao động cần tìm là \[x=4\sqrt{3}\cos \left( 4\pi t-\frac{2\pi }{3} \right)cm\]
Chọn đáp án D
Câu 13: Một vật dao động điều hòa dọc theo trục Ox với biên độ 4 cm, chu kì 2 s. Tại thời điểm t = 0,25 s, vật có vận tốc \[v=-2\pi \sqrt{2}cm/s\], gia tốc a > 0. Phương trình dao động của vật là:
A.\[x=4\cos \left( 2\pi t+0,5\pi \right)cm\]
B.\[x=4\cos \left( \pi t+0,5\pi \right)cm\]
C.\[x=4\cos \left( \pi t-0,5\pi \right)cm\]
D.\[x=4\cos \left( 2\pi t-0,5\pi \right)cm\]
Hướng dẫn
Phương trình tổng quát cần tìm \[x=A\cos \left( \omega t+\varphi \right)\]
Bài cho A=4cm; \[\omega =\pi rad/s\]
Tại t=0,25s ta có: \[{{A}^{2}}={{x}^{2}}+{{\left( \frac{v}{\omega } \right)}^{2}}\Rightarrow \left| x \right|=2\sqrt{2}cm\]
Có a>0 => x<0 =>\[x=-2\sqrt{2}cm\]
\[\to {{\varphi }_{0,25(s)}}=\frac{3\pi }{4}rad\]
Ta có: \[{{\varphi }_{0,25(s)}}=\pi .0,25+\varphi =\frac{3\pi }{4}rad\Leftrightarrow \varphi =\frac{\pi }{2}rad\]
Vậy phương trình dao động cần tìm là \[x=4\cos \left( \pi t+0,5\pi \right)cm\]
Chọn đáp án B
Câu 14: Hai vật dao động điều hòa dọc theo các trục song song với nhau. Phương trình dao động của các vật lần lượt là \[{{x}_{1}}={{A}_{1}}\cos \left( {{\omega }_{1}}t+{{\varphi }_{1}} \right)cm\] và \[{{x}_{2}}={{A}_{2}}\cos \left( {{\omega }_{2}}t+{{\varphi }_{2}} \right)cm\]. Biết \[x_{1}^{2}+x_{2}^{2}=50\left( c{{m}^{2}} \right)\] . Tại thời điểm t, hai vật đi ngược chiều nhau và vật thứ nhất đi qua vị trí có li độ \[{{x}_{1}}=-1cm\] . Khi đó vật thứ hai có li độ là
A. 7 cm. B. - 7 cm. C.\[\pm 7cm\] D.\[\pm 1cm\]
Khi \[{{x}_{1}}=-1cm\] thì \[{{x}_{2}}=-7cm\] nhưng do 2 vật chuyển động ngược chiều nhau nên \[{{x}_{2}}=-7cm\]
Chọn đáp án B
Câu 15: Một chất điểm dao động điều hòa trên trục Ox. Khi chất điểm đi qua vị trí cân bằng thì tốc độ của nó là 20 cm/s. Khi chất điểm có tốc độ là 10 cm/s thì gia tốc của nó có độ lớn là \[40\sqrt{3}cm/{{s}^{2}}\]. Biên độ dao động của chất điểm là
A. 5 cm. B. 4 cm. C. 10 cm. D. 8 cm.
Ta có:\[\frac{{{v}^{2}}}{{{\omega }^{2}}}+\frac{{{a}^{2}}}{{{\omega }^{4}}}={{A}^{2}}\]
Khi qua VTCB nên a=0 nên \[v={{v}_{\max }}=20cm/s\]
Ta có: \[\frac{{{v}^{2}}}{{{\left( A\omega \right)}^{2}}}+\frac{{{a}^{2}}}{{{\left( {{A}^{2}}\omega \right)}^{4}}}=1\to \omega =4rad/s\]
Biên độ: \[A=\frac{{{v}_{\max }}}{\omega }=5cm\]
Chọn đáp án A







