Lí Thuyết Sóng Cơ

LÍ THUYẾT SÓNG CƠ

 

I.SÓNG CƠ VÀ SỰ TRUYỀN SÓNG CƠ :

1.Sóng cơ- Định nghĩa- phân loại

+ Sóng cơ  là những dao động  lan truyền  trong môi trường .

 + Khi sóng cơ truyền đi chỉ có pha dao động của các phần tử vật chất lan truyền còn các phần tử vật chất thì dao động xung quanh vị trí cân bằng cố định.

 + Sóng ngang là sóng trong đó các phần tử của môi trường dao động theo phương vuông góc với phương truyền sóng. Ví dụ: sóng trên mặt nước, sóng trên sợi dây cao su.

 + Sóng dọc là sóng trong đó các phần tử của môi trường dao động theo phương  trùng với phương truyền sóng.            

   Ví dụ: sóng âm, sóng trên một lò xo.

2.Các đặc trưng của một sóng hình sin

 + Biên độ của sóng A: là biên độ dao động của một phần tử   của môi trường có sóng truyền qua.

 + Chu kỳ sóng T: là chu kỳ dao động  của một  phần tử  của môi trường  sóng truyền qua.

 + Tần số  f: là đại lượng nghịch đảo của chu kỳ sóng : \[f=\frac{1}{T}\]

 + Tốc độ  truyền sóng v : là tốc độ lan truyền  dao động trong môi trường  .

 + Bước sóng l: là quảng đường mà sóng  truyền được trong một chu kỳ.\[\lambda =vT=\frac{v}{f}\]    

 +Bước sóng l cũng là khoảng cách giữa hai điểm gần nhau nhất trên phương truyền sóng dao động cùng pha.

 +Khoảng cách giữa hai điểm gần nhau nhất trên phương  truyền sóng mà dao động ngược pha là \[\frac{\lambda }{2}\].

 +Khoảng cách giữa hai điểm gần nhau nhất trên phương  truyền sóng mà dao động vuông pha là  \[\frac{\lambda }{4}\].

 +Khoảng cách giữa hai điểm bất kỳ  trên phương  truyền sóng mà dao động cùng pha là:  kl.

 +Khoảng cách giữa hai điểm bất kỳ  trên phương  truyền sóng mà dao động ngược pha là: (2k+1)\[\frac{\lambda }{2}\].

 +Lưu ý: Giữa n đỉnh (ngọn) sóng có (n - 1) bước sóng.

3. Phương trình sóng:

 

a.Tại nguồn O: \[{{u}_{0}}={{A}_{0}}\cos \omega t\]

b.Tại M trên phương truyền sóng:

\[{{u}_{M}}={{A}_{M}}\cos \omega (t-\Delta t)\]

Nếu bỏ qua mất mát năng lượng trong quá trình truyền sóng thì biên độ sóng tại O và  M bằng nhau: A_o = A_M = A.

Thì:\[{{u}_{M}}={{A}_{M}}\cos \omega (t-\frac{x}{v})\]

c.Tổng quát: Tại điểm O: \[{{u}_{0}}={{A}_{0}}\cos (\omega t+\varphi )\]

d.Tại điểm M cách O một đoạn x trên phương truyền sóng.

   * Sóng truyền theo chiều dương của trục Ox thì:

\[{{u}_{M}}={{A}_{M}}\cos (\omega t+\varphi -\omega \frac{x}{v})={{A}_{M}}\cos (\omega t+\varphi -2\pi \frac{x}{\lambda })\]

   * Sóng truyền theo chiều âm của trục Ox thì:  

\[{{u}_{M}}={{A}_{M}}\cos (\omega t+\varphi +\omega \frac{x}{v})={{A}_{M}}\cos (\omega t+\varphi +2\pi \frac{x}{\lambda })\]

-Tại một điểm M xác định trong môi trường sóng: x =const; u_M là hàm điều hòa theo t với chu kỳ T.

-Tại một thời điểm  xác định t= const ; u_M là hàm  biến thiên điều hòa theo không gian  x với chu kỳ l.

e. Độ lệch pha giữa hai điểm cách nguồn một khoảng x_M, x_N:    

$\Delta {{\varphi }_{MN}}=\omega \frac{{{x}_{N}}-{{x}_{M}}}{v}=2\pi \frac{{{x}_{N}}-{{x}_{M}}}{\lambda }$  

+Nếu  2 điểm M và N dao động cùng pha thì:

$\Delta {{\varphi }_{MN}}=2k\pi <=>2\pi \frac{{{x}_{N}}-{{x}_{M}}}{\lambda }=2k\pi <=>{{x}_{N}}-{{x}_{M}}=k\lambda $.      ( k Î Z )

+Nếu  2 điểm M và N dao động ngược pha thì:

$\Delta {{\varphi }_{MN}}=(2k+1)\pi <=>2\pi \frac{{{x}_{N}}-{{x}_{M}}}{\lambda }=(2k+1)\pi <=>{{x}_{N}}-{{x}_{M}}=(2k+1)\frac{\lambda }{2}$.  ( k Î Z )

+Nếu  2 điểm M và N dao động vuông pha thì:

$\Delta {{\varphi }_{MN}}=(2k+1)\frac{\pi }{2}<=>2\pi \frac{{{x}_{N}}-{{x}_{M}}}{\lambda }=(2k+1)\frac{\pi }{2}<=>{{x}_{N}}-{{x}_{M}}=(2k+1)\frac{\lambda }{4}$. ( k Î Z )

-Nếu 2 điểm M và N  nằm trên một phương truyền sóng và cách nhau một khoảng x thì:$\Delta \varphi =\omega \frac{x}{v}=2\pi \frac{x}{\lambda }$

     (Nếu  2 điểm M và N trên phương truyền sóng và cách nhau một khoảng d  thì :  Dj = )

 - Vậy 2 điểm M và N trên phương truyền sóng sẽ:

+ dao động cùng pha khi:  d = kl                        

+ dao động ngược pha khi:          d = (2k + 1) l/2

+ dao động vuông pha khi:          d = (2k + 1) l/4

                                                      với k = 0, ±1, ±2 ...

           Lưu ý: Đơn vị của x, x₁, x₂,d,  l  và  v phải tương ứng với nhau.

f. Trong hiện tượng truyền sóng trên sợi dây, dây được kích thích dao động bởi nam châm điện với tần số dòng điện là f thì tần số dao động của dây là 2f.

II. GIAO THOA SÓNG

1. Điều kiện để có giao thoa:

Hai sóng là hai sóng kết hợp tức là hai sóng cùng tần số và có độ lệch pha không đổi theo thời gian (hoặc hai sóng cùng pha).

2. Lý thuyết giao thoa:

Giao thoa của hai sóng phát ra từ hai nguồn sóng kết hợp S₁, S₂ cách nhau một khoảng l:

+Phương trình sóng tại 2 nguồn :(Điểm M cách hai nguồn lần lượt d₁, d₂)

   ${{u}_{1}}=\text{Acos}(2\pi ft+{{\varphi }_{1}})$ và ${{u}_{2}}=\text{Acos}(2\pi ft+{{\varphi }_{2}})$

+Phương trình sóng tại M do hai sóng từ hai nguồn truyền tới:

   ${{u}_{1M}}=\text{Acos}(2\pi ft-2\pi \frac{{{d}_{1}}}{\lambda }+{{\varphi }_{1}})$ và ${{u}_{2M}}=\text{Acos}(2\pi ft-2\pi \frac{{{d}_{2}}}{\lambda }+{{\varphi }_{2}})$

+Phương trình giao thoa sóng tại M: u_M = u_1M + u_2M

   ${{u}_{M}}=2Ac\text{os}\left[ \pi \frac{{{d}_{1}}-{{d}_{2}}}{\lambda }+\frac{\Delta \varphi }{2} \right]c\text{os}\left[ 2\pi ft-\pi \frac{{{d}_{1}}+{{d}_{2}}}{\lambda }+\frac{{{\varphi }_{1}}+{{\varphi }_{2}}}{2} \right]$

+Biên độ dao động tại M: \[{{A}_{M}}=2A\left| c\text{os}\left( \pi \frac{{{d}_{1}}-{{d}_{2}}}{\lambda }+\frac{\Delta \varphi }{2} \right) \right|\] với $\Delta \varphi ={{\varphi }_{2}}-{{\varphi }_{1}}$

 

2.1.Tìm số điểm dao động cực đại, số điểm dao động cực tiểu giữa hai nguồn:

Cách 1 :

  * Số cực đại:  $-\frac{l}{\lambda }+\frac{\Delta \varphi }{2\pi }

* Số cực tiểu: \[-\frac{l}{\lambda }-\frac{1}{2}+\frac{\Delta \varphi }{2\pi }

Cách 2:

Ta lấy: S₁S₂/l = n, p (n nguyên dương, p phần thập phân sau dấu phảy)

Số cực đại luôn là: 2n +1( chỉ đối với hai nguồn cùng pha)

Số cực tiểu là:+Trường hợp 1: Nếu p<5   thì số cực tiểu là 2n.

                       +Trường hợp 2: Nếu p ³ 5 thì số cức tiểu là 2n+2.

Nếu hai nguồn dao động ngược pha thì  làm ngược lại.

2.2. Hai nguồn dao động cùng pha ($\Delta \varphi ={{\varphi }_{1}}-{{\varphi }_{2}}=0$ hoặc 2kp)

+ Độ lệch pha của hai sóng thành phần tại M:\[\Delta \varphi =\frac{2\pi }{\lambda }({{d}_{2}}-{{d}_{1}})\]

+ Biên độ sóng tổng hợp:  \[{{A}_{M}}=2.A.\left| \cos \frac{\pi }{\lambda }.({{d}_{2}}-{{d}_{1}}) \right|\]

  v A_max= 2.A khi:+ Hai sóng thành phần tại M cùng pha « Dj=2.k.p (kÎZ)

                              + Hiệu đường đi d = d₂ – d₁= k.l

  v A_min= 0     khi:+ Hai sóng thành phần tại M ngược pha nhau « Dj=(2.k+1)p (kÎZ)

                              + Hiệu đường đi d=d₂ – d₁=(k + 1/2).l

+ Khoảng cách giữa hai đỉnh liên tiếp của hai hypecbol cùng loại (giữa hai cực đại (hai cực tiểu) giao thoa): l/2.

+ Số đường dao động với A_max và A_min :

    v Số đường dao động với A_max (luôn là số lẻ) là số giá trị của k thỏa mãn điều kiện

         (không tính hai nguồn):

        * Số Cực đại:     $-\frac{l}{\lambda }ÎZ.

   Vị trí của các điểm cực đại giao thoa xác định bởi

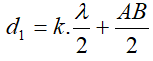:(thay các giá trị tìm được của k vào)

    v Số đường dao động với A_min (luôn là số chẵn) là số giá trị của k thỏa mãn điều kiện

      (không tính hai nguồn):

        * Số Cực tiểu:   $-\frac{l}{\lambda }-\frac{1}{2} và kÎ Z.

                          Hay  \[-\frac{l}{\lambda }

   Vị trí của các điểm cực tiểu giao thoa xác định bởi:

(thay các giá trị  của k vào).

  ® Số cực đại giao thoa bằng số cực tiểu giao thoa + 1.

2.3. Hai nguồn dao động ngược pha:($\Delta \varphi ={{\varphi }_{1}}-{{\varphi }_{2}}=\pi $)

   * Điểm dao động cực đại:  d₁ – d₂ = (2k+1)$\frac{\lambda }{2}$ (kÎZ)

  Số đường hoặc số điểm dao động cực đại (không tính hai nguồn):

      $-\frac{l}{\lambda }-\frac{1}{2}

   * Điểm dao động cực tiểu (không dao động):d₁ – d₂ = kl (kÎZ)

   Số đường hoặc số điểm dao động cực tiểu (không tính hai nguồn):

      \[-\frac{l}{\lambda }

 

2.4. Hai nguồn dao động vuông pha: Dj =(2k+1)p/2 ( Số Cực đại= Số Cực tiểu)

 + Phương trình hai nguồn kết hợp:  

 + Phương trình sóng tổng hợp tại M: \[u=2.A.\cos \left[ \frac{\pi }{\lambda }\left( {{d}_{2}}-{{d}_{1}} \right)-\frac{\pi }{4} \right]\cos \left[ \omega .t-\frac{\pi }{\lambda }\left( {{d}_{1}}+{{d}_{2}} \right)+\frac{\pi }{4} \right]\]

 +  Độ lệch pha của hai sóng thành phần tại M: \[\Delta \phi =\frac{2\pi }{\lambda }\left( {{d}_{2}}-{{d}_{1}} \right)-\frac{\pi }{2}\]

 + Biên độ sóng tổng hợp:  A_M = \[u=2.A.\left| \cos \left[ \frac{\pi }{\lambda }\left( {{d}_{2}}-{{d}_{1}} \right)-\frac{\pi }{4} \right] \right|\]

   * Số Cực đại: \[-\frac{l}{\lambda }+\frac{1}{4}    

   * Số Cực tiểu:\[-\frac{l}{\lambda }-\frac{1}{4}  

                  Hay  \[-\frac{l}{\lambda }

    

Nhận xét: số điểm cực đại và cực tiểu trên đoạn AB là bằng nhau nên có thể dùng 1 công thức là đủ

=> Số giá trị nguyên của k thoả mãn các biểu thức trên là số đường cần tìm.

 

2.5.Tìm số điểm dao động cực đại, dao động cực tiểu giữa hai điểm M N:

   Các công thức tổng quát :

a. Độ lệch pha của hai sóng từ hai nguồn đến M là:

       \[\Delta {{\varphi }_{M}}={{\varphi }_{2M}}-{{\varphi }_{1M}}=\frac{2\pi }{\lambda }({{d}_{1}}-{{d}_{2}})+\Delta \varphi \]    (1)  

   với \[\Delta {{\varphi }_{{}}}={{\varphi }_{2}}-{{\varphi }_{1}}\]

b. Hiệu đường đi của sóng từ hai nguồn đến M là:

       \[({{d}_{1}}-{{d}_{2}})=(\Delta {{\varphi }_{M}}-\Delta \varphi )\frac{\lambda }{2\pi }\]    (2)

-Chú ý:  + \[\Delta {{\varphi }_{{}}}={{\varphi }_{2}}-{{\varphi }_{1}}\]   là độ lệch pha của hai sóng thành phần của nguồn 2 so với nguồn 1

              + \[\Delta {{\varphi }_{M}}={{\varphi }_{2M}}-{{\varphi }_{1M}}\]là độ lệch pha của hai sóng thành phần tại M của nguồn 2 so với nguồn 1

do sóng từ nguồn 2 và nguồn 1 truyền đến

c. Số điểm (đường) dao động cực đại, cực tiểu giữa hai điểm M, N thỏa mãn :

        Dd_M £ \[({{d}_{1}}-{{d}_{2}})=(\Delta {{\varphi }_{M}}-\Delta \varphi )\frac{\lambda }{2\pi }\]£  Dd_N     (3)

( Hai điểm M, N cách hai nguồn lần lượt là d_1M, d_2M, d_1N, d_2N. )

  Ta đặt Dd_M= d_1M - d_2M ; Dd_N = d_1N - d_2N, giả sử: Dd_M < Dd_N

Với số giá trị nguyên của k thỏa mãn biểu thức trên là số điểm (đường)  cần tìm giữa hai điểm M và N.

Chú ý: Trong công thức (3) Nếu M hoặc N trùng với nguồn thì không dủng dấu BẰNG

(chỉ dùng dấu < )  Vì nguồn là điểm đặc biệt không phải là điểm cực đại hoặc cực tiểu!

d.Tìm số đường dao động cực đại và không dao động giữa hai điểm M, N bất kỳ

Hai điểm M, N  cách hai nguồn lần lượt là d_1M, d_2M, d_1N, d_2N.

Đặt Dd_M = d_1M - d_2M ; Dd_N = d_1N - d_2N và giả sử Dd_M < Dd_N.

   + Hai nguồn dao động cùng pha:

 * Cực đại:  Dd_M < kl   < Dd_N

 * Cực tiểu: Dd_M < (k+0,5)l < Dd_N

   + Hai nguồn dao động ngược pha:

 * Cực đại:  Dd_M < (k+0,5)l < Dd_N

 * Cực tiểu: Dd_M < kl  < Dd_N

         Số giá trị nguyên của k thoả mãn các biểu thức trên là số đường cần tìm.

III. SÓNG DỪNG

     - Định Nghĩa: Sóng dừng là sóng có các nút(điểm luôn đứng yên) và các bụng (biên độ dao động cực đại) cố định trong không gian

     - Nguyên nhân: Sóng dừng là kết quả của sự giao thoa giữa sóng tới và sóng phản xạ, khi sóng tới và sóng phản xạ truyền theo cùng một phương.

1. Một số chú ý

* Đầu cố định hoặc đầu dao động nhỏ là nút sóng. Đầu tự do là bụng sóng

* Hai điểm đối xứng với nhau qua nút sóng luôn dao động ngược pha.

* Hai điểm đối xứng với nhau qua bụng sóng luôn dao động cùng pha.

* Các điểm trên dây đều dao động với biên độ không đổi Þ năng lượng không truyền đi

* Bề rông 1 bụng là 4A, A là biên độ sóng tới hoặc sóng phản xạ.

* Khoảng thời gian giữa hai lần sợi dây căng ngang (các phần tử đi qua VTCB) là nửa chu kỳ.

2. Điều kiện để có sóng dừng trên sợi dây dài l:

* Hai đầu là nút sóng: $l=k\frac{\lambda }{2}\text{  }(k\in {{N}^{*}})$

   Số bụng sóng = số bó sóng = k ;    Số nút sóng = k + 1

Một đầu là nút sóng còn một đầu là bụng sóng:     

                   $l=(2k+1)\frac{\lambda }{4}\text{  }(k\in N)$

  Số bó (bụng) sóng nguyên = k; Số bụng sóng = số nút sóng = k + 1

3 Đặc điểm của sóng dừng:

   -Khoảng cách giữa 2 nút hoặc 2 bụng liền kề là \[\frac{\lambda }{2}\] 

   -Khoảng cách giữa nút và bụng liền kề là \[\frac{\lambda }{4}\]

   -Khoảng cách giữa hai nút (bụng, múi) sóng bất kỳ là : \[k\frac{\lambda }{2}\]

   -Tốc độ  truyền sóng:\[v=\lambda f=\frac{\lambda }{T}\] 

4. Phương trình sóng dừng trên sợi dây (đầu P cố định hoặc dao động nhỏ là nút sóng)

* Đầu Q cố định (nút sóng):

Phương trình sóng tới và sóng phản xạ tại Q: ${{u}_{B}}=Ac\text{os2}\pi ft$ và $u{{'}_{B}}=-Ac\text{os2}\pi ft=Ac\text{os(2}\pi ft-\pi )$

Phương trình sóng tới và sóng phản xạ tại M cách Q một khoảng d là:

${{u}_{M}}=Ac\text{os(2}\pi ft+2\pi \frac{d}{\lambda })$ và $u{{'}_{M}}=Ac\text{os(2}\pi ft-2\pi \frac{d}{\lambda }-\pi )$

Phương trình sóng dừng tại M: ${{u}_{M}}={{u}_{M}}+u{{'}_{M}}$

${{u}_{M}}=2Ac\text{os}(2\pi \frac{d}{\lambda }+\frac{\pi }{2})c\text{os}(2\pi ft-\frac{\pi }{2})=2A\text{sin}(2\pi \frac{d}{\lambda })c\text{os}(2\pi ft+\frac{\pi }{2})$

Biên độ dao động của phần tử tại M: ${{A}_{M}}=2A\left| c\text{os}(2\pi \frac{d}{\lambda }+\frac{\pi }{2}) \right|=2A\left| \text{sin}(2\pi \frac{d}{\lambda }) \right|$

* Đầu Q tự do (bụng sóng):

Phương trình sóng tới và sóng phản xạ tại Q: ${{u}_{B}}=u{{'}_{B}}=Ac\text{os2}\pi ft$

Phương trình sóng tới và sóng phản xạ tại M cách Q một khoảng d là:

${{u}_{M}}=Ac\text{os(2}\pi ft+2\pi \frac{d}{\lambda })$ và $u{{'}_{M}}=Ac\text{os(2}\pi ft-2\pi \frac{d}{\lambda })$

Phương trình sóng dừng tại M: ${{u}_{M}}={{u}_{M}}+u{{'}_{M}}$;  ${{u}_{M}}=2Ac\text{os}(2\pi \frac{d}{\lambda })c\text{os}(2\pi ft)$

Biên độ dao động của phần tử tại M: ${{A}_{M}}=2A\left| \text{cos}(2\pi \frac{d}{\lambda }) \right|$

Lưu ý: * Với x là khoảng cách từ M đến đầu nút sóng thì biên độ:    ${{A}_{M}}=2A\left| \text{sin}(2\pi \frac{x}{\lambda }) \right|$

            * Với x là khoảng cách từ M đến đầu bụng sóng thì biên độ:${{A}_{M}}=2A\left| \text{cos}(2\pi \frac{x}{\lambda }) \right|$

IV. SÓNG ÂM

1. Sóng âm:

   Sóng âm là những sóng cơ  truyền trong môi trường khí, lỏng, rắn.Tần số của sóng âm là tần số âm.

 +Âm nghe được có tần số từ 16Hz đến 20000Hz và gây ra cảm giác âm trong tai con người.

 +Hạ âm : Những sóng cơ học tần số nhỏ hơn 16Hz gọi là sóng hạ âm, tai người không nghe được

 +siêu âm :Những sóng cơ học tần số lớn hơn 20000Hz gọi là sóng siêu âm , tai người không nghe được.

2. Các đặc tính vật lý của  âm

 a.Tần số âm: Tần số của của sóng âm cũng là tần số âm .

 b.+ Cường độ âm: $\text{I=}\frac{\text{W}}{\text{tS}}\text{=}\frac{\text{P}}{\text{S}}$Cường độ âm tại 1 điểm cách nguồn một đoạn R: $\text{I=}\frac{\text{P}}{4\pi {{R}^{2}}}$

    Với W (J), P (W) là năng lượng, công suất phát âm của nguồn.S (m²) là diện tích mặt vuông góc với phương truyền âm      (với sóng cầu thì S là diện tích mặt cầu S=4πR²)

  + Mức cường độ âm:

  $L(B)=lg\frac{I}{{{I}_{0}}}$ =>$\frac{I}{{{I}_{0}}}={{10}^{L}}$ Hoặc $L(dB)=10.lg\frac{I}{{{I}_{0}}}$ =>  ${{L}_{2}}-{{L}_{1}}=lg\frac{{{I}_{2}}}{{{I}_{0}}}-lg\frac{{{I}_{1}}}{{{I}_{0}}}=lg\frac{{{I}_{2}}}{{{I}_{1}}}<=>\frac{{{I}_{2}}}{{{I}_{1}}}={{10}^{{{L}_{2}}-{{L}_{1}}}}$

Với I₀ = 10^-12 W/m² gọi là cường độ âm chuẩn  ở f = 1000Hz

   Đơn vị của mức cường độ âm là Ben (B), thường dùng đềxiben (dB):    1B = 10dB.      

 c.Âm cơ bản và hoạ âm : Sóng âm do một nhạc cụ phát ra là tổng hợp của nhiều sóng âm phát ra cùng một lúc. Các sóng này có tần số là f, 2f, 3f, ….Âm có tần số f là hoạ âm cơ bản, các âm có tần số 2f, 3f, … là các hoạ âm thứ 2, thứ 3, …. Tập hợp các hoạ âm tạo thành phổ  của nhạc âm nói trên

 -Đồ thị dao động âm : của cùng một nhạc âm do các nhạc cụ khác nhau phát ra thì hoàn toàn khác nhau.

 

3. Các nguồn  âm thường gặp:

+Dây  đàn: Tần số do đàn phát ra (hai đầu dây cố định Þ hai đầu là nút sóng)

 $f=k\frac{v}{2l}\text{  ( k}\in \text{N*)}$.  Ứng với k = 1 Þ  âm phát ra âm cơ bản có tần số ${{f}_{1}}=\frac{v}{2l}$

                                            k = 2,3,4… có các hoạ âm bậc 2 (tần số 2f₁), bậc 3 (tần số 3f₁)…

 +Ống sáo: Tần số do ống sáo phát ra (một đầu bịt kín (nút sóng), một đầu để hở (bụng sóng)

                                            Þ ( một đầu là nút sóng, một đầu là bụng sóng)

$f=(2k+1)\frac{v}{4l}\text{  ( k}\in \text{N)}$. Ứng với k = 0 Þ  âm phát ra âm cơ bản có tần số ${{f}_{1}}=\frac{v}{4l}$

                                           k = 1,2,3… có các hoạ âm bậc 3 (tần số 3f₁), bậc 5 (tần số 5f₁)…

.

..

Bài viết gợi ý: