BÀI TẬP CON LẮC LÒ XO
Câu 1: Một con lắc lò xo gồm vật nặng có khối lượng \[\sqrt{2}\] kg dao động điều hòa theo phương ngang. Vận tốc của vật có độ lớn cực đại là 0,6 m/s. Chọn gốc thời gian t = 0 là lúc vật đi qua vị trí \[{{x}_{0}}=3\sqrt{2}\]cm và tại đó thế năng của lò xo có độ lớn bằng động năng của vật. Tính chu kì dao động của con lắc và độ lớn lực đàn hồi cực đại tại thời điểm \[t=\frac{\pi }{20}s\]
A. 0,628 s và 3 N B. 0,314 s và 3 N C. 0,314 và 6 N D. 0,628 s và 6 N
Hướng dẫn
+ Vị trí \[{{x}_{0}}=3\sqrt{2}\]là vị trí động năng bằng thế năng, ta có \[\frac{\sqrt{2}}{2}A=3\sqrt{2}\Rightarrow A=6cm\]
+ Tốc độ cực đại của vật \[{{v}_{max}}=\omega A\Leftrightarrow 60=\omega 6\Rightarrow \omega =10\] rad/s \[\Rightarrow T=\frac{2\pi }{\omega }=\frac{\pi }{5}\approx 0,628s\]
+ Ta để ý rằng từ thời điểm ban đầu đến thời điểm \[t=\frac{\pi }{20}=\frac{T}{A}\Rightarrow x=\sqrt{{{A}^{2}}-x_{0}^{2}}=\sqrt{{{6}^{2}}-{{\left( 3\sqrt{2} \right)}^{2}}}=3\sqrt{2}\] cm
Độ lớn của lực đàn hồi tại vị trí này
\[F=kx=m{{\omega }^{2}}x=\sqrt{2}{{.10}^{2}}.3\sqrt{2}{{.10}^{-2}}=6N\]
- Đáp án D
Câu 2: Một con lắc lò xo treo thẳng đứng. Chiều dài tự nhiên của lò xo là 20 cm. Khi vật ở vị trí cân bằng thì lò xo giãn 4 cm. Lực đàn hồi cực đại và cực tiểu mà lò xo tác dụng vào vật là 10 N và 6 N. Chiều dài cực đại và cực tiểu của lò xo trong quá trình vật dao động là
A. 25 cm và 24 cm B. 24 cm và 23 cm C. 26 cm và 24 cm D. 25 cm và 23 cm
Hướng dẫn
Ta có tỉ số
\[\frac{{{F}_{d{{h}_{max}}}}}{{{F}_{d{{h}_{\min }}}}}=\frac{\Delta {{l}_{0}}+A}{\Delta {{l}_{0}}-A}\Leftrightarrow \frac{4+A}{4-A}=\frac{10}{6}\Rightarrow A=1cm\]
Chiều dài cực đại và cực tiểu của lò xo là
.png)
- Đáp án D
Câu 3: Một con lắc lò xo treo thẳng đứng gồm vật nặng có khối lượng m = 100 g và lò xo có độ cứng k = 40 N/m. Nâng vật nặng lên theo phương thẳng đứng bằng một lực 1,2 N cho tới khi quả cầu đứng yên rồi thả nhẹ để vật dao động điều hòa. Lấy g = 10 m/s2. Lực đàn hồi cực đại và cực tiểu của vật tác dụng lên giá treo là
A. 1,2 N và 0 N B. 2,2 N và 0 N C. 1,2 N và 0,2 N D. 2,2 N và 0,2 N
Hướng dẫn
|
vị trí quả cầu đứng yên khi được nâng lên thẳng đứng, ta có + Độ biến dạng của lò xo tại vị trí cân bằng \[\Delta {{l}_{0}}=\frac{mg}{k}=\frac{{{100.10}^{-2}}.10}{40}=2,5cm\] + Tại \[{{F}_{dh}}=F-P\Leftrightarrow \Delta l=\frac{F-P}{k}=\frac{1,2-{{100.10}^{-3}}.10}{40}=0,5cm\] Vậy khi thả nhẹ con lắc sẽ dao động với biên độ \[A=2,5+0,5=3cm\](lưu ý rằng tại vị trí cân bằng này lò xo đang bị nén) + Lực đàn hồi cực đại và cực tiểu tác dụng lên giá treo
|
|
- Đáp án B
Câu 4: Một con lắc lò xo treo thẳng đứng dao động điều hòa với phương trình li độ \[x=8\cos \left( 10t+\pi \right)\]cm (gốc tọa độ được chọn tại vị trí cân bằng, chiều đương hướng lên). Lấy g = 10 = π2 m/s2. Thời gian ngắn nhất để độ lớn của lực đàn hồi tăng từ cực đại đến cực tiểu là
A. \[\frac{\pi }{10}s\] B. \[\frac{\pi }{15}s\] C. \[\frac{\pi }{30}s\] D. \[\frac{3\pi }{10}s\]
Hướng dẫn
|
+ Độ biến dạng của lò xo tại vị trí cân bằng \[\Delta {{l}_{0}}=\frac{g}{{{\omega }^{2}}}=\frac{10}{{{10}^{2}}}=10cm\] Ta thấy rằng \[\Delta {{l}_{0}}>A\]\[\Rightarrow \]lực đàn hồi cực đại tại vị trí lò xo giãn nhiều nhất (biên âm) và cực tiểu tại vị trí lò xo giãn ít nhất (biên dương), khoảng thời gian ngắn nhất để vật đi giữa hai vị trí này là \[t=\frac{T}{2}=\frac{\pi }{10}s\] |
|
- Đáp án A
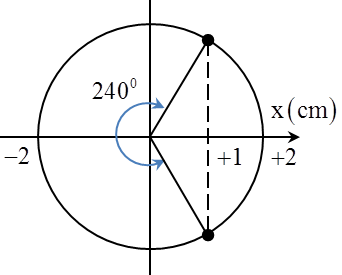
Câu 5: Một con lắc lò xo dao động điều hòa theo phương thẳng đứng với biên độ 2 cm và tần số góc \[\omega =10\sqrt{5}\] rad/s, biết lò xo có độ cứng 50 N/m. Lấy g = 10 m/s2. Trong mỗi chu kì, thời gian để lực đàn hồi của lò xo có độ lớn không vượt quá 1,5 N là
A. \[\frac{\pi }{60\sqrt{5}}s\] B. \[\frac{2\pi }{15\sqrt{5}}s\] C. \[\frac{\pi }{15\sqrt{5}}s\] D. \[\frac{\pi }{30\sqrt{5}}s\]
Hướng dẫn
|
+ Độ biến dạng của lò xo tại vị trí cân bằng \[\Delta {{l}_{0}}=\frac{g}{{{\omega }^{2}}}=\frac{10}{{{\left( 10\sqrt{5} \right)}^{2}}}=2cm\] Ta thấy rằng \[A=\Delta {{l}_{0}}\], trong quá trình dao động lò xo luôn giãn, lực đàn hồi có độ lớn 1,5 N tại vị trí lò xo giãn \[\Delta l=\frac{F}{k}=\frac{1,5}{50}=3cm\], tương ứng với li độ \[x=1cm\] + Từ hình vẽ, ta xác đinh được khoảng thời gian trong một chu kì lực đàn hồi có độ lớn nhỏ hơn 1,5 N là \[t=\frac{2T}{3}=\frac{2\pi }{15\sqrt{5}}s\]
|
|
Câu 6: Một con lắc lò xo dao động điều hòa theo phương thẳng đứng với chu kì dao động 0,5 s. Kích thích cho con lắc dao động điều hòa với biên độ gấp hai lần độ giãn của lò xo tại vị trí cân bằng. Lấy g = 10 m/s2. Khoảng thời gian ngắn nhất giữa hai lần gia tốc của vật có độ lớn bằng gia tốc rơi tự do là
A. \[\frac{1}{8}s\] B. \[\frac{1}{6}s\] C. \[\frac{1}{12}s\] D. \[\frac{3}{8}s\]
Hướng dẫn
|
Gia tốc của vật \[\left| a \right|={{\omega }^{2}}\left| x \right|=g\Leftrightarrow \frac{g}{\Delta {{l}_{0}}}\left| x \right|=g\Rightarrow \left| x \right|=\Delta {{l}_{0}}=\frac{A}{2}\] Từ hình vẽ, ta xác định được khoảng thời gian tương ứng là \[t=\frac{T}{6}=\frac{1}{12}s\]
|
|
Câu 7: Một con lắc lò xo treo thẳng đứng, gồm vật nặng m = 200 g, lò xo nhẹ có độ cứng k = 50 N/m. Từ vị trí cân bằng kéo vật xuống dưới để lò xo giãn 12 cm rồi thả nhẹ cho vật dao động điều hòa. Lấy g = 10 = π2 m/s2. Khoảng thời gian ngắn nhất giữa hai lần liên tiếp lực đàn hồi của lò xo bằng 0 là
A. \[\frac{1}{10}s\] B. \[\frac{1}{15}s\] C. \[\frac{2}{15}s\] D. \[\frac{4}{15}s\]
Hướng dẫn
|
Độ biến dạng của lò xo tại vị trí cân bằng \[\Delta {{l}_{0}}=\frac{mg}{k}=\frac{{{200.10}^{-3}}.10}{50}=4cm\] + Kéo vật đến vị trí lò xo giãn 12 cm rồi thả nhẹ, sau đó vật sẽ dao động với biên độ A = 8 cm + Lực đàn hồi của lò xo bằng 0 tại vị trí \[x=-\Delta {{l}_{0}}=-4cm\] Thời gian tương ứng \[t=\frac{T}{3}=\frac{2}{15}s\]
|
|
Câu 8: Một con lắc lò xo treo thẳng đứng, từ vị trí cân bằng kéo vật xuống phía dưới để lò xo giãn 10 cm rồi thả nhẹ. Sau khoảng thời gian nhỏ nhất tương ứng là Δt1, Δt2 thì lực phục hồi và lực đàn hồi của lò xo triệt tiêu, với \[\frac{\Delta {{t}_{1}}}{\Delta {{t}_{2}}}=\frac{3}{4}\]. Lấy Lấy g = 10 m/s2. Chu kì dao động của con lắc là
A. 0,68 s B. 0,15 s C. 0,76 s D. 0,44 s
Hướng dẫn
|
Từ vị trí cân bằng, kéo lò xo xuống một đoạn 10 cm rồi thả nhẹ \[\Rightarrow A=10cm\] + Lực phục hồi triệt tiêu tại vị trí cân bằng \[\Delta {{t}_{1}}=\frac{T}{4}\] + Lực đàn hồi triệt tiêu khi vật đi qua vị trí lò xo không giãn \[\Delta {{t}_{2}}=\frac{4}{3}\Delta {{t}_{1}}=\frac{4}{3}\frac{T}{4}=\frac{T}{3}\Rightarrow \Delta {{l}_{0}}=\frac{A}{2}=5cm\] Vậy chu kì dao động của con lắc là \[T=2\pi \sqrt{\frac{\Delta {{l}_{0}}}{g}}=2\pi \sqrt{\frac{{{5.10}^{-2}}}{10}}=0,44s\]
|
|
Câu 9: Một con lắc lò xo treo thẳng đứng dao động điều hòa với chu kì T = 0,6 s trong trường trọng lực. Biết trong mỗi chu kì có 3 lần lực đàn hồi của lò xo có độ cứng bằng trọng lượng của vật. Thời gian lò xo bị nén trong mỗi chu kì là
A. 0,1 s B. 0,2 s C. 0,15 s D. 0,3 s
Hướng dẫn
|
Hai vị trí ứng với ba lần để lực đàn hồi của lò xo có độ lớn bằng trọng lực là vị trí cân bằng và vị trí biên trên cho trường hợp \[A=2\Delta {{l}_{0}}\] Lò xo bị nén khi vật nằm trong khoảng li độ \[-A\le x\le -\Delta {{l}_{0}}\] Từ hình vẽ ta có \[t=\frac{T}{3}=0,2s\]
|
|
Câu 10: Một con lắc lò xo treo thẳng đứng có k = 100 N/m, vật nặng m = 100 g, lấy g = 10 = π2 m/s2. Từ vị trí cân bằng kéo vật xuống dưới một đoạn 1 cm rồi truyền cho vật vận tốc ban đầu \[10\pi \sqrt{3}\]cm/s hướng thẳng đứng. Tỉ số giữa thời gian lò xo nén và giãn trong một chu kì
A. 0,5 B. 2 C. 0,2 D. 5
Hướng dẫn
|
Độ biến dạng của lò xo tại vị trí cân bằng \[\Delta {{l}_{0}}=\frac{mg}{k}=\frac{{{100.10}^{-3}}.10}{100}=1cm\] + Biên độ dao động của vật \[A=\sqrt{{{x}^{2}}+{{\left( \frac{v}{\omega } \right)}^{2}}}=\sqrt{{{1}^{2}}+{{\left( \frac{10\pi \sqrt{3}}{10\pi } \right)}^{2}}}=2cm\] Lò xo bị nén khi vật nằm trong khoảng li độ \[-A\le x\le -\Delta {{l}_{0}}\], thời gian còn lại lò xo sẽ giãn Từ hình vẽ ta thấy \[\frac{{{t}_{n}}}{{{t}_{g}}}=\frac{{{\varphi }_{n}}}{{{\varphi }_{g}}}=0,5\]
|
|
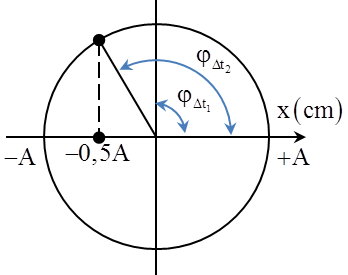
Câu 11: (Chuyên Vĩnh Phúc) Một con lắc lò xo treo thẳng đứng gồm quả cầu nhỏ có khối lượng \[m=150\]g và lò xo có độ cứng \[k=60\]N/m. Người ta đưa quả cầu đến vị trí lò xo không bị biến dạng rồi truyền cho nó một vận tốc ban đầu \[{{v}_{0}}=\frac{\sqrt{3}}{2}\]m/s theo phương thẳng đứng hướng xuống. Sau khi được truyền vận tốc con lắc dao động điều hòa. Lúc \[t=0\] là lúc quả cầu được truyền vận tốc, lấy \[g=10\]m/s2. Thời gian ngắn nhất tính từ lúc\[t=0\] đến lúc lực đàn hồi tác dụng lên vật có độ lớn 3N là
A. \[\frac{\pi }{60}s\] B. \[\frac{\pi }{20}s\] C. \[\frac{\pi }{30}s\] D. \[\frac{\pi }{5}s\]
Hướng dẫn
|
Tần số góc của dao động \[\omega =\sqrt{\frac{k}{m}}=20\]rad/s Độ giãn của lò xo khi con lắc nằm cân bằng \[\Delta {{l}_{0}}=\frac{mg}{k}=2,5\]cm Tại vị trí lò xo không bị biến dạng \[x=-2,5\]cm người ta truyền cho con lắc vận tốc ban đầu \[{{v}_{0}}=\frac{\sqrt{3}}{2}\]m/s \[\Rightarrow A=\sqrt{{{x}^{2}}+{{\left( \frac{v}{\omega } \right)}^{2}}}=5\]cm Vị trí lò xo có lực đàn hồi 3 N ứng với độ giãn \[\Delta l=\frac{F}{k}=5\]cm \[\Rightarrow \]con lắc đang ở vị trí \[x=2,5\]cm Phương pháp đường tròn Từ hình vẽ ta xác định được khoảng thời gian ứng với góc quét\[\varphi =\frac{\pi }{3}rad\Rightarrow t=\frac{\varphi }{\omega }=\frac{\pi }{60}s\]
|
|
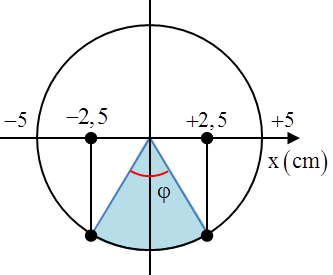
Câu 12: (THPT Ngọc Tảo) Một con lắc lò xo treo thẳng đứng tại nơi có gia tốc trọng trường \[g=10\]m/s2, đầu trên của lò xo gắn cố định, đầu dưới gắn với vật nặng có khối lượng m. Kích thích cho con lắc dao động điều hòa theo phương thẳng đứng với chu kì T. Khoảng thời gian lò xo bị nén trong một chu kì là \[\frac{T}{6}\]. Tại thời điểm vật đi qua vị trí lò xo không bị biến dạng thì tốc độ của vật là \[10\sqrt{3}\pi \]cm/s. Lấy \[{{\pi }^{2}}=10\]chu kì dao động của con lắc là
A. 0,5 s B. 0,2 s C. 0,6 s D. 0,4 s
Hướng dẫn
|
+ Trong một chu kì, lò xo bị nén khi con lắc di chuyển trong khoảng \[-A\le x\le \Delta {{l}_{0}}\], thời gian lò xo bị nén \[t=\frac{T}{6}\] ứng với góc quét \[\varphi =\frac{\pi }{3}\]rad + Phương pháp đường tròn Từ hình vẽ ta có \[\cos \frac{\pi }{6}=\frac{\Delta {{l}_{0}}}{A}\Rightarrow \Delta {{l}_{0}}=\frac{\sqrt{3}}{2}A\]\[\Rightarrow {{v}_{\max }}=\omega A=\frac{10\sqrt{3}\pi }{\cos \frac{\pi }{6}}=20\sqrt{3}\pi \]cm/s Biến đổi \[{{v}_{\text{max}}}=\omega A=\sqrt{\frac{g}{\Delta {{l}_{0}}}}\frac{2\Delta {{l}_{0}}}{\sqrt{3}}=\frac{2}{\sqrt{3}}\sqrt{g\Delta {{l}_{0}}}\]\[\Rightarrow \Delta {{l}_{0}}=\frac{3v_{\max }^{2}}{4g}\] Chu kì của con lắc \[T=2\pi \sqrt{\frac{\Delta {{l}_{0}}}{g}}=0,6s\]
|
|
Câu 13: (Chuyên Vĩnh Phúc – 2017) Một con lắc lò xo dao động điều hòa theo phương thẳng đứng dọc theo trục Ox có gốc tọa độ trùng với vị trí cân bằng của vật. Tại thời điểm lò xo giãn a m thì tốc độ của vật là \[v\sqrt{8}\]m/s; tại thời điểm lò xo giãn 2a m thì tốc độ của vật là \[v\sqrt{6}\]m/s và tại thời điểm lò xo giãn 3a m thì tốc độ của vật là \[v\sqrt{2}\]m/s. Biết tại O lò xo giãn một khoảng nhỏ hơn a. Tỉ số tốc độ trung bình của vật khi lò xo nén và khi lò xo giãn trong một chu kì xấp xỉ bằng
A. 0,88 B. 0,78 C. 0,67 D. 1,25
Hướng dẫn
|
Gọi \[\Delta l{}_{0}\] là độ biến dạng của lò xo tại vị trí cân bằng Ta có
|
|
Chuẩn hóa
.png)
Lò xo sẽ bị nén khi vật nằm trong khoảng li độ \[-A\le x\le -\Delta {{l}_{0}}\]
Thời gian là xo bị nén ứng với góc α, với \[\text{cos}\left( \frac{\alpha }{2} \right)=\frac{\Delta {{l}_{0}}}{A}=\frac{1}{\sqrt{41}}\]
Tỉ số thời gian lò xo bị nén và bị giãn \[\frac{{{T}_{g}}}{{{T}_{n}}}=\frac{2\pi -\alpha }{\alpha }=1,2218\]
Tỉ số tốc độ trung bình giữa \[\frac{{{v}_{n}}}{{{v}_{g}}}=\frac{{{S}_{n}}}{{{S}_{g}}}\frac{{{T}_{g}}}{{{T}_{n}}}=\frac{2\text{A}-2\Delta {{l}_{0}}}{2A+2\Delta {{l}_{0}}}\frac{{{T}_{g}}}{{{T}_{n}}}=\frac{\sqrt{41}-1}{\sqrt{41}+1}1,2218=0,89\]
- Đáp án A
.png)
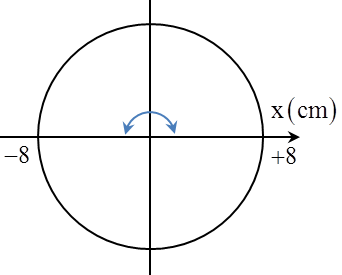

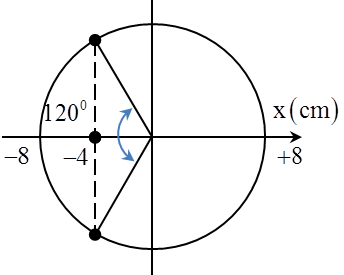
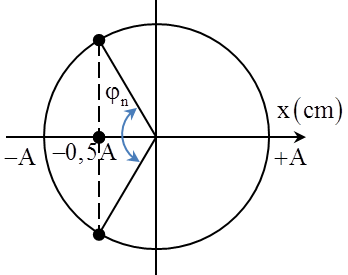
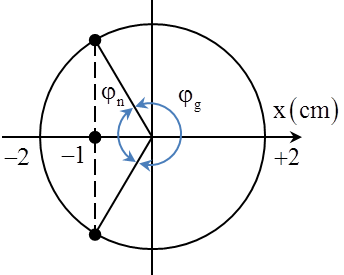
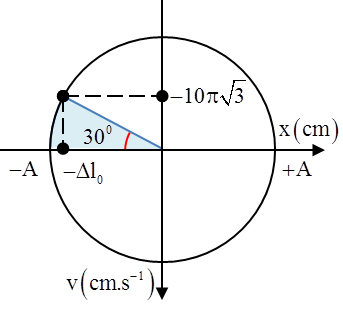
.png)