BÀI TOÁN CẮT GHÉP LÒ XO
A: KIẾN THỨC CẦN NHỚ
I. CẮT GHÉP LÒ XO
1. Ghép hai lò xo:
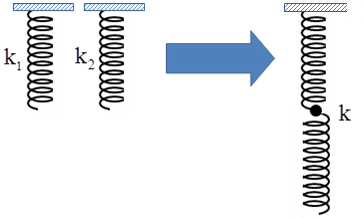
+ Với hai lò xo có độ cứng k1 và k2 thì ta thường có hai cách ghép là nối tiếp và song song
|
Ghép nối tiếp |
Ghép song song |
|
Với cách ghép nối tiếp, ta có \[\frac{1}{k}=\frac{1}{{{k}_{1}}}+\frac{1}{{{k}_{2}}}\] |
Với cách ghép song song, ta có \[k={{k}_{1}}+{{k}_{2}}\] |
2. Cắt lò xo:
+ Giả sử với một lò xo ban đầu có chiều dài l, độ cứng k. Ta tiến hành cắt lò xo này này các lò xo có chiều dài l1 độ cứng k1, chiều dài l2 độ cứng k2..........
Khi đó độ cứng của các lò xo sẽ tỉ lệ nghịch với chiều dài
\[kl={{k}_{1}}{{l}_{1}}={{k}_{2}}{{l}_{2}}=....={{k}_{n}}l{}_{n}\]
II. BÀI TOÁN XÁC ĐỊNH BIÊN ĐỘ DAO ĐỘNG MỚI CỦA CON LẮC LÒ XO SAU KHI CỐ ĐỊNH MỘT ĐIỂM TRÊN LÒ XO
Bài toán: Một con lắc lò xo gồm lò xo đang dao động điều hòa theo phương ngang với biên độ A. Đúng lúc con lắc đi qua vị trí động năng bằng n lần thế năng thì ta tiến hành cố định lò xo tại điểm M sao cho hệ dao động mới với lò xo có chiều dài \[{l}'=\frac{l}{m}\]. Xác định tỉ số giữa biên độ dao động mới và biên độ dao động cũ \[\frac{{{A}'}}{A}\]
Hướng dẫn:
+ Tại thời điểm cố định lò xo ta có
.png)
+ Vì thế năng đàn hồi của lò xo phân bố đều trên mỗi đơn vị chiều dài, do vậy thế năng của hệ dao động mới là
\[{{{E}'}_{t}}=\frac{{{E}_{t}}}{m}=\frac{E}{m\left( n+1 \right)}\]
+ Cơ năng của hệ dao động mới
\[{E}'={{{E}'}_{t}}+{{{E}'}_{d}}\Leftrightarrow \frac{1}{2}\underbrace{{{k}'}}_{mk}{{{A}'}^{2}}=\frac{E}{m\left( n+1 \right)}+\frac{nE}{n+1}\]
Biến đổi toán học ta thu được tỉ số: \[\frac{{{A}'}}{A}=\sqrt{\frac{\left( mn+1 \right)}{2m\left( n+1 \right)}}\]
B:BÀI TậP
Câu 1: Hai lò xo L1 và L2 có cùng chiều dài. Khi treo vật m vào lò xo L1 thì chu kì dao động của vật là T1 = 0,3 s, khi treo vật m vào lò xo L2 thì chu kì dao động của vật là T2 = 0,4 s. Ghép hai lò xo này song song với nhau, tiếp tục treo vật m lên hệ thì chu kì dao động của vật là
A. 0,12 s B. 0,24 s C. 0,36 s D. 0,48 s
Hướng dẫn
Ta có \[T\sim \frac{1}{\sqrt{k}}\]
Kết hợp với \[{{k}_{ss}}={{k}_{1}}+{{k}_{2}}\Rightarrow \frac{1}{T_{ss}^{2}}=\frac{1}{T_{1}^{2}}+\frac{1}{T_{2}^{2}}\Rightarrow {{T}_{ss}}=\frac{{{T}_{1}}{{T}_{2}}}{\sqrt{T_{1}^{2}+T_{2}^{2}}}=\frac{0,3.0,4}{\sqrt{{{0,3}^{2}}+{{0,4}^{2}}}}=0,24s\]
- Đáp án B
Câu 2: Khi treo vật khối lượng m vào lò xo k1 thì chu kì dao động của vật là T1 = 0,8 s. Nếu treo vật vào lò xo có độ cứng k2 thì vật dao động điều hòa với chu kì T2 = 0,6 s. Treo vật m vào hệ hai lò xo ghép song song thì chu kì dao động của vật là
A. 0,48 s B. 0,1 s C. 0,7 s D. 0,14 s
Hướng dẫn
Ta có \[T\sim \frac{1}{\sqrt{k}}\]
Kết hợp với \[{{k}_{ss}}={{k}_{1}}+{{k}_{2}}\Rightarrow \frac{1}{T_{ss}^{2}}=\frac{1}{T_{1}^{2}}+\frac{1}{T_{2}^{2}}\Rightarrow {{T}_{ss}}=\frac{{{T}_{1}}{{T}_{2}}}{\sqrt{T_{1}^{2}+T_{2}^{2}}}=\frac{0,6.0,8}{\sqrt{{{0,6}^{2}}+{{0,8}^{2}}}}=0,48s\]
- Đáp án A
Câu 3: Treo vật m vào một lò xo và kích thích cho vật dao động với biên độ A. Tiến hành lấy hai lò xo giống hệt nhau này ghép nối tiếp, treo vật m lên hệ lò xo mới với kích thích cho vật dao động với năng lượng như cũ. Biên độ dao động mới của hệ
A. 2A B. \[\sqrt{2}A\] C. 0,5A D. 4A
Hướng dẫn
Độ cứng của lò xo mới tương ứng \[\frac{1}{{{k}_{nt}}}=\frac{1}{k}+\frac{1}{k}\Rightarrow {{k}_{nt}}=\frac{k}{2}\]
Theo giả thuyết của bài toán
\[{{E}_{2}}={{E}_{1}}\Leftrightarrow \frac{1}{2}{{k}_{nt}}A_{2}^{2}=\frac{1}{2}kA\Leftrightarrow \frac{1}{2}\frac{k}{2}A_{2}^{2}=\frac{1}{2}kA\Rightarrow {{A}_{2}}=\sqrt{2}A\]
- Đáp án B
Câu 4: Một lò xo có độ cứng 50 N/m, khi mắc vào vật m thì hệ này dao động với chu kì 1 s, người ta cắt lò xo thành hai phần bằng nhau rồi ghép hai lò xo song song lại với nhau, gắn vật trên vào hệ lò xo mới và cho dao động thì hệ này có chu ki là
A. 0,5 s B. 0,25 s C. 4s D. 2 s
Hướng dẫn
Độ cứng của lò xo khi cắt thành hai đoạn bằng nhau rồi ghép song song
\[{{k}_{ss}}=2k+2k=4k\]N/m
+ Kết hợp với \[T\sim \sqrt{k}\xrightarrow{{{k}_{ss}}=4k}{{T}_{ss}}=2T=2s\]
- Đáp án D
Câu 5: Hai lò xo L1 và L2 có cùng chiều dài tự nhiên L0. Khi treo vật có khối lượng m = 0,8 kg vào lò xo L1 thì chu kì dao động của vật là T1 = 0,3 s, khi treo vào lò xo L2 thì chu kì dao động của vật là T2 = 0,4 s. Ghép nối tiếp hai lò xo này lại với nhau. Muốn chu kì dao động của hệ là 0,35 s thì phải tăng hay giảm khối lượng của vật đi bao nhiêu?
A. tăng them 40,8 g B. tăng them 408 g C. giảm đi 408 g D. giảm đi 40,8 g
Hướng dẫn
Ta có \[T\sim \sqrt{\frac{m}{k}}\]
Độ cứng của lò xo khi ghép nối tiếp \[\frac{1}{{{k}_{nt}}}=\frac{1}{{{k}_{1}}}+\frac{1}{{{k}_{2}}}\], vậy nếu giữ nguyên khối lượng thì chu kì dao động mới của con lắc là \[{{T}_{nt}}=\sqrt{T_{1}^{2}+T_{2}^{2}}=\sqrt{{{0,3}^{2}}+{{0,4}^{2}}}=0,5s\]
+ Ta có tỉ số:
\[{{\left( \frac{{{T}'}}{{{T}_{nt}}} \right)}^{2}}=\frac{{{m}'}}{m}\Leftrightarrow {{\left( \frac{0,35}{0,5} \right)}^{2}}\Rightarrow {m}'=m{{\left( \frac{0,35}{0,5} \right)}^{2}}=0,8{{\left( \frac{0,35}{0,5} \right)}^{2}}=0,392kg\]
Vậy ta phải giảm khối lượng của vật 408 g
- Đáp án C
Câu 6: Một quả cầu nhỏ, khi gắn vào lò xo có độ cứng k thì hệ dao động với chu kì T. Biết độ cứng của lò xo tỉ lệ nghịch với chiều dài của nó. Hỏi phải cắt lò xo trên thành bao nhiêu phần bằng nhau để khi treo quả cầu vào mỗi phần đó thì chu kì dao động của hệ là 0,25T
A. 16 phần B. 8 phần C. 4 phần D. 12 phần
Hướng dẫn
Ta có \[T\sim \frac{1}{\sqrt{k}}\xrightarrow{{T}'=\frac{T}{4}}{k}'=16k\Rightarrow \]ta phải cắt lò xo thành 16 phần
- Đáp án A
Câu 7: Một con lắc lò xo được cấu tạo bởi một lò xo đồng chất và có chiều dài tự nhiên là l, vật nhỏ có khối lượng m. Chu kì dao động riêng của con lắc là 3,0 s. Nết cắt ngắn lò xo đi 30 cm thì chu kì dao động riêng của con lắc là 1,5 s. Độ dài ban đầu của lò xo là
A. 30 cm B. 50 cm C. 40 cm D. 60 cm
Hướng dẫn
Ta có \[{{\left( \frac{T}{{{T}'}} \right)}^{2}}=\frac{{{k}'}}{k}={{\left( \frac{3}{1,5} \right)}^{2}}=4\]
Chiều dài của lò xo tỉ lệ nghịch với độ cứng nên
\[\frac{{{l}'}}{{{l}_{0}}}=\frac{{{l}_{0}}-30}{{{l}_{0}}}=\frac{1}{4}\Rightarrow {{l}_{0}}=40cm\]
- Đáp án C
Câu 8: Hai lò xo có độ cứng lần lượt là k1 và k2. Khi treo vật có khối lượng m = 425 g vào hai lò xo này ghép nối tiếp thì chu kì dao động của vật là 0,65 s. Khi treo vật vào hai lò xo này ghép song song thì chu kì dao động của vật là \[\frac{3}{13}s\]. Chu kì dao động của vật khi lần lượt treo trên các lò xo k1 và k2
A. 0,35 s và 0,6 s B. 0,25 s và 0,6 s C. 0,4 s và 0,5 s D. 0,2 s và 0,35 s
Hướng dẫn
Độ cứng của lò xo ứng với các cách ghép
.png)
+ Từ giả thuyết bài toán, ta có hệ phương trình
.png)
Vậy k1 và k2 là nghiệm của phương trình
.png)
- Đáp án B
Câu 9: Hai lò xo nhẹ có độ cứng k1 và k2 có cùng chiều dài được treo thẳng đứng, đầu trên cố định, đầu dưới treo các vật m1 (gắn với k1), m2 = 4m1 (gắn với k2). Cho hai vật dao động điều hòa theo phương thẳng đứng khi đó chu kì dao động của vật lần lượt là T1 = 0,6 s và T2 = 0,4 s. Mắc hai lò xo trên nối tiếp với nhau, đầu trên cố định, đầu dưới treo vật m2. Tần số dao động của vật m2 khi đó là
A. 2,4 Hz B. 2 Hz C. 1 Hz D. 0,5 Hz
Hướng dẫn
Ta có tỉ số
\[\frac{{{T}_{1}}}{{{T}_{1}}}=\sqrt{\frac{{{m}_{1}}{{k}_{2}}}{{{m}_{2}}{{k}_{1}}}}\Rightarrow \frac{{{k}_{1}}}{{{k}_{2}}}=\frac{{{m}_{1}}}{{{m}_{2}}}{{\left( \frac{{{T}_{2}}}{{{T}_{1}}} \right)}^{2}}=4{{\left( \frac{0,4}{0,6} \right)}^{2}}=\frac{16}{9}\]
Độ cứng của lò xo ghi ghép nối tiếp \[{{k}_{nt}}=\frac{{{k}_{1}}{{k}_{2}}}{{{k}_{1}}+{{k}_{2}}}=\frac{\frac{16}{9}{{k}_{2}}{{k}_{2}}}{\frac{16}{9}{{k}_{2}}+{{k}_{2}}}=\frac{16}{25}{{k}_{2}}\]
\[f\sim \sqrt{k}\xrightarrow{{{k}_{nt}}=\frac{16}{25}{{k}_{2}}}{{f}_{nt}}=0,8{{f}_{2}}=2Hz\]
- Đáp án B
Câu 10: Một con lắc lò xo gồm vật nặng có khối lượng m = 100 g, và lò xo có độ cứng k = 100 N/m đặt nằm ngang. Từ vị trí cân bằng truyền cho vật một vận tốc ban đầu để vật dao động điều hòa, chọn gốc thời gian là lúc truyền vận tốc cho vật. Tại thời điểm t = 0,15 s giữ cố định điểm chính giữa của lò xo. Vật tiếp tục dao động với biên độ
A. 0,5A B. 2A C. 3A D. 4A
Hướng dẫn
Chu kì dao động của con lắc \[T=2\pi \sqrt{\frac{m}{k}}=2\pi \sqrt{\frac{{{100.10}^{-3}}}{100}}=0,2s\]
+ Sau khoảng thời gian \[t=\frac{3T}{4}=0,15s\] vật đang ở vị trí biên, ở vị trí này thế năng của lò xo chính bằng cơ năng \[E=\frac{1}{2}k{{A}^{2}}\], động năng của con lắc bằng 0
+ Giữ điểm chính giữa của lò xo lại, hệ dao động mới với lò xo có độ cứng \[{k}'=2k\]\[\Rightarrow \] thế năng của con lắc cũng chính là cơ năng giảm một nửa \[{E}'=\frac{E}{2}\Rightarrow \frac{1}{2}2k{{{A}'}^{2}}=\frac{1}{2}\frac{1}{2}k{{A}^{2}}\Rightarrow {A}'=\frac{A}{2}\]
Đáp án A
Câu 11: Một con lắc lò xo dao động điều hòa theo phương ngang với biên độ A. Đúng lúc con lắc đi qua vị trí động năng bằng thế năng và đang giãn thì người ta tiến hành cố định điểm chính giữa của lò xo, sau khi cố định hệ con lắc mới dao động với biên độ \[{A}'\]. Giá trị của \[{A}'\] là
A. \[\frac{\sqrt{6}}{4}A\] B. \[0,5A\] C. \[\frac{\sqrt{3}}{8}A\] D. \[\frac{\sqrt{3}}{2}A\]
Hướng dẫn
Tại vị trí động năng bằng thế năng \[{{E}_{d}}={{E}_{t}}=\frac{E}{2}\]
+ Khi cố định điểm chính giữa của lò xo thì hệ dao động mới có độ cứng của lò xo là 2k và
.png)
- Đáp án A
Câu 12: Một con lắc lò xo dao động điều hòa theo phương ngang với biên độ A. Đúng lúc con lắc đi qua vị trí động năng bằng thế năng và đang giãn thì người ta tiến hành cố định điểm chính giữa của lò xo, sau khi cố định hệ con lắc mới dao động với biên độ \[{A}'\]. Giá trị của \[{A}'\] là
A. \[\frac{\sqrt{6}}{4}A\] B. \[0,5A\] C. \[\frac{\sqrt{3}}{8}A\] D. \[\frac{\sqrt{3}}{2}A\]
Hướng dẫn
Tại vị trí cân bằng \[{{E}_{d}}=E\]
+ Người ta giữ lò xo tại vị trí các đầu cố định \[\frac{1}{3}\]chiều dài \[\Rightarrow \]hệ dao động mới với lò xo có độ cứng \[{k}'=\frac{3}{2}k\]
Trong cả hai trường hợp động năng của vật đều bằng nhau và đúng bằng cơ năng do vậy
\[{E}'=E\Leftrightarrow \frac{1}{2}{k}'{{{A}'}^{2}}=\frac{1}{2}k{{A}^{2}}\Rightarrow A=\sqrt{\frac{k}{{{k}'}}}A=\sqrt{\frac{2}{3}}A\]
Đáp án A
Câu 13: Một con lắc lò xo dao động điều hòa theo phương ngang với tốc độ cực đại là 40 cm/s. Khi vật đi qua vị trí biên người ta tiến hành giữ cố định điểm chính giữa của lò xo lại. Kể từ thời điểm đó vật sẽ dao động điều hòa với tốc độ cực đại là
A. \[20\sqrt{2}\]cm/s B. 20 cm/s C. \[40\sqrt{2}\]cm/s D. \[10\sqrt{2}\]cm/s
Hướng dẫn
Tại vị trí biên thế năng đàn hồi chính là cơ năng của con lắc \[{{E}_{t}}=E\]
+ Người ta giữ vị trí chính giữa của lò xo thì hệ dao động mới có độ cứng của lò xo là \[{k}'=2k\]
Thế năng của con lắc bằng cơ năng và bằng một nửa giá trị đầu
\[{{{E}'}_{t}}={E}'=0,5{{E}_{t}}=0,5E\Leftrightarrow \frac{1}{2}2k{{{A}'}^{2}}=0,5\frac{1}{2}k{{A}^{2}}\Rightarrow {A}'=\frac{A}{2}\]
Tốc độ cực đại của con lắc \[{{{v}'}_{max}}={\omega }'{A}'=\sqrt{2}\omega \frac{A}{2}=\frac{\sqrt{2}}{2}{{v}_{max}}=20\sqrt{2}\]cm/s
- Đáp án A
Câu 14: Một con lắc lò xo đang dao động điều hòa trên mặt phẳng nằm ngang với biên độ bằng 5 cm và tần số 5 Hz. Khi vật đi qua vị trí có li độ 4 cm thì ta tiến hành giữ cố định điểm chính giữa của lò xo. Sau thời điểm đó, biên độ dao động của vật là
A. 2,92 cm B. 3,83 cm C. 2,45 cm D. 2 cm
Hướng dẫn
Tốc độ của vật khi vừa mới giữ điểm chính giữa
\[{{v}_{0}}=\omega \sqrt{{{A}^{2}}-{{x}^{2}}}=2\pi .5\sqrt{{{5}^{2}}-{{4}^{2}}}=30\pi \]cm/s
+ Biên độ dao động mới của con lắc
\[{A}'=\sqrt{x_{0}^{2}+{{\left( \frac{{{v}_{0}}}{{{\omega }'}} \right)}^{2}}}=\sqrt{{{2}^{2}}+{{\left( \frac{30\pi }{2\pi .5\sqrt{2}} \right)}^{2}}}=2,92cm\]
- Đáp án A
Câu 15: Một con lắc lò xo dao động điều hòa theo phương ngang với quỹ đạo có chiều dài 16 cm. Khi vật m đang chuyển động theo chiều làm lò xo giãn đến vị trí động năng bằng thế năng người ta chốt cố định điểm chính giữa của lò xo. Sau đó vật m sẽ dao động với biên độ
A. \[8\sqrt{3}cm\] B. \[2\sqrt{6}cm\] C. 4 cm D. \[4\sqrt{3}\]cm
Hướng dẫn
Biên độ dao động của vật \[A=\frac{L}{2}=\frac{16}{2}=8\]cm
+ Tại vị trí động năng bằng thế năng người ta chốt điểm giữa của lò xo, cơ hệ mới với lò xo có độ cứng 2k, ta có.png)
- Đáp án B