KÍCH THÍCH DAO ĐỘNG CỦA VẬT BẰNG NGOẠI LỰC-VA CHẠM
A: KIẾN THỨC CẦN CÓ
I. KÍCH THÍCH DAO ĐỘNG CỦA VẬT BẰNG NGOẠI LỰC
Bài toán: Một con lắc lò xo đang dao động điều hòa theo phương ngang với biên độ A. Tại thời điểm t0 khi vật đi qua vị trí có li độ x0 và tốc độ v0, tác dụng lên vật một lực \[\overrightarrow{F}\] không đổi trong khoảng thời gian Δt. Xác định biên độ dao động của vật ngay sau khi ngừng tác dụng lực \[\overrightarrow{F}\]
Phân tích:
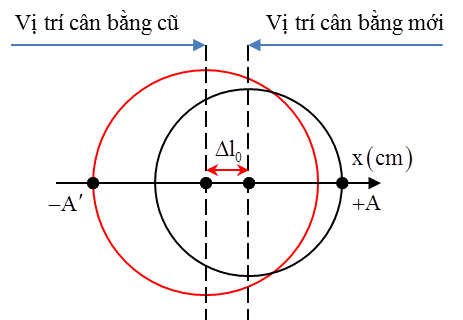
+ Dưới tác dụng của ngoại lực \[\overrightarrow{F}\] vật sẽ dao động điều hòa quanh vị trí cân bằng mới, vị trí này cách vị trí cân bằng cũ một đoạn Δl0.
+ Khi ngừng tác dụng lực \[\overrightarrow{F}\], vật lại dao động quanh vị trí cân bằng cũ
Như vậy điểm quan trọng của bài toán trên là xác định vị trí cân bằng của từng giai đoạn dao động tương ứng qua đó xác định các đại lượng li độ, vận tốc ứng với mỗi vị trí cân bằng từ đó tìm được biên độ của dao động.
|
|
Hướng dẫn:
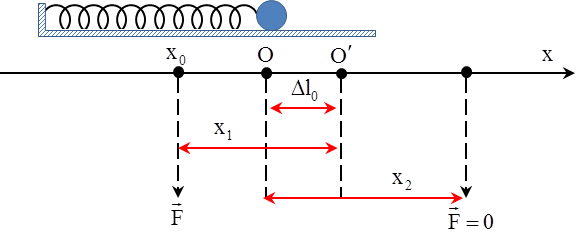
+ Bước 1: Xác định độ biến dạng của lò xo tại vị trí cân bằng mới \[\Delta {{l}_{0}}=\frac{F}{k}\]
+ Bước 2: Biên độ dao động của vật trong khoảng thời gian lực \[\overrightarrow{F}\] tác dụng \[{{A}_{1}}=\sqrt{x_{1}^{2}+{{\left( \frac{{{v}_{0}}}{\omega } \right)}^{2}}}\] với x1 là khoảng cách từ vật đến vị trí cân bằng mới \[{O}'\]
+ Bước 3: Xác định li độ và tốc độ của vật sau khoảng thời gian Δt
+ Bước 4: Biên độ dao động của vật\[{{A}_{2}}=\sqrt{x_{2}^{2}+{{\left( \frac{{{v}_{02}}}{\omega } \right)}^{2}}}\] với x2 là khoảng cách từ vật đến vị trí cân bằng cũ O
II. KÍCH THÍCH DAO ĐỘNG BẰNG VA CHẠM MỀM
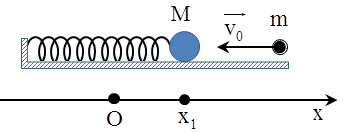
Bài toán: Một con lắc lò xo gồm lò xo với vật nặng có khối lượng M đang dao động điều hòa với biên độ A và tần số góc ω. Khi vật đi qua vị trí có li độ x1 và vận tốc v1 thì một vật có khối lượng m bay theo phương trục của lò xo với vận tốc v0 đến va chạm mềm với M. Biên độ dao động của hệ sau va chạm
Hướng dẫn:
|
Con lắc lò xo nằm ngang |
Con lắc lò xo treo thẳng đứng |
||
|
Ta nhận thấy rằng quá trình va chạm này không làm thay đổi vị trí cân bằng của hệ mà chỉ làm thay đổi tần số góc của dao động + Tần số góc của hệ sau va chạm \[{\omega }'=\sqrt{\frac{k}{M+m}}\] + Vận tốc của hệ vật sau va cham \[\overrightarrow{{{V}_{0}}}=\frac{M\overrightarrow{{{v}_{1}}}+m\overrightarrow{{{v}_{0}}}}{M+m}\] + Biên độ dao động mới của hệ \[{A}'=\sqrt{x_{1}^{2}+{{\left( \frac{{{V}_{0}}}{{{\omega }'}} \right)}^{2}}}\]
|
|
B: BÀI TậP
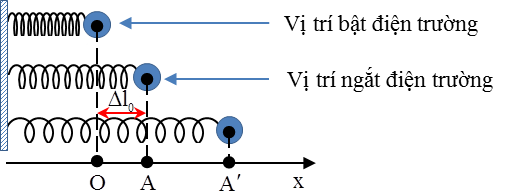
Câu 1: (THPT Ngô Sỹ Liên) Một con lắc lò xo nằm ngang gồm vật nặng khối lượng 100 g, tích điện \[q={{5.10}^{-6}}C\] và lò xo có độ cứng k = 10 N/m. Khi vật đang ở vị trí cân bằng, người ta kích thích dao động bằng cách tạo ra một điện trường đều theo phương nằm ngang dọc theo trục của lò xo và có cường độ \[E={{10}^{4}}\]V/m trong khoảng thời gian \[\Delta t=0,05\pi \]s rồi ngắt điện trường. Bỏ qua mọi ma sát. Tính năng lượng dao động của con lắc khi ngắt điện trường
A. 0,5 J B. 0,0375 J C. 0,025 J D. 0,0125 J
Hướng dẫn
|
|
Tần số góc của dao động \[\omega =\sqrt{\frac{k}{m}}=10\]rad/s
Chu kì của dao dao động này là \[T=\frac{2\pi }{\omega }=0,2\pi \]s\[\Rightarrow \Delta t=\frac{T}{4}\]
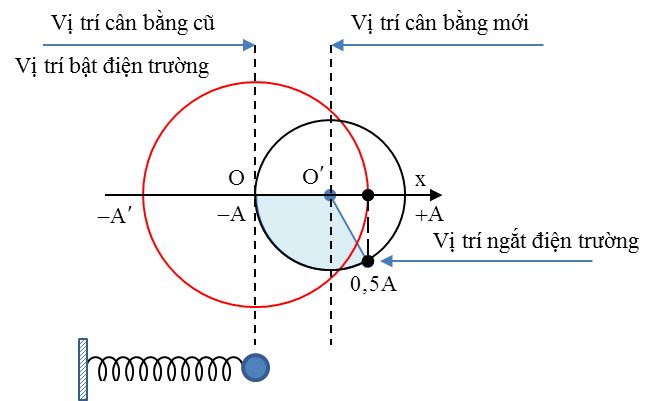
+ Tại vị trí mà người ta bật điện trường, sau kích thích con lắc dao động điều hòa quanh vị trí cân bằng mới, vị trí này lực đàn hồi cân bằng với lực điện, khi đó lò xo đã giãn một đoạn \[\Delta {{l}_{0}}=\frac{qE}{k}={{5.10}^{-3}}m\Rightarrow A={{5.10}^{-3}}m\]
Từ vị trí cân bằng này sau khoảng thời gian \[\Delta t=\frac{T}{4}\] con lắc đến vị trí cân bằng \[\Rightarrow v=\omega A\]
+ Tại lại tiếp tục ngắt điện trường, con lắc sẽ dao động điều hòa quanh vị trí cân bằng cũ với biên độ \[{A}'=\sqrt{{{A}^{2}}+{{\left( \frac{v}{\omega } \right)}^{2}}}=5\sqrt{2}\]cm
Năng lượng dao động lúc này \[E=\frac{1}{2}k{{{A}'}^{2}}=0,025J\]
Đáp án C
Câu 2: (THPT Lý Thái Tổ - Bắc Ninh) Trong thang máy có treo một con lắc lò xo với độ cứng 25 N/m, vật nặng có khối lượng 400 g. Khi thang máy đang đứng yên ta cho con lắc dao động điều hòa, chiều dài của con lắc thay đổi từ 32 cm đến 48 cm. Tại thời điểm mà vật ở vị trí thấp nhất thì cho thang máy đi xuống nhanh dần đều với gia tốc \[a=\frac{g}{10}\]. Lấy \[g={{\pi }^{2}}\]m/s2. Biên độ dao động của vật trong trường hợp này là
A. 17 cm B. 19,2 cm C. 8,5 cm D. 9,6 cm
Hướng dẫn
|
|
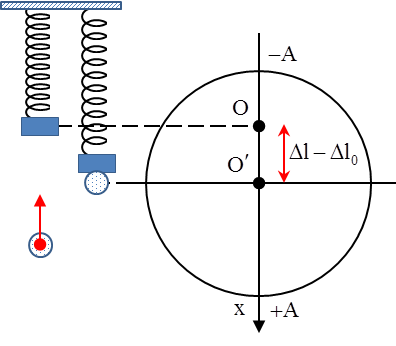
Độ giãn của lò xo tại vị trí cân bằng \[\Delta {{l}_{0}}=\frac{mg}{k}=16cm\]
Biên độ dao đông của con lắc khi thang máy đứng yên \[A=\frac{{{l}_{\max }}-{{l}_{\min }}}{2}=8\]cm
+ Tại vị trí thấp nhất ta cho thang máy chuyển động xuống dưới nhanh dần đều, ta có thể xem con lắc chuyển động trong trường trọng lực biểu kiến với \[{{P}_{bk}}=m\left( g-a \right)\]
Khi đó con lắc sẽ dao động điều hòa quanh vị trí cân bằng mới, vị trí này lực đàn hồi cân bằng với trọng lực biểu kiến \[{{P}_{bk}}=k\Delta l\Rightarrow \Delta l=\frac{m\left( g-a \right)}{k}=14,4cm\]
Biên độ dao động mới của con lắc \[{A}'=\sqrt{{{\left( A+\Delta {{l}_{0}}-\Delta l \right)}^{2}}+{{\left( \frac{v}{\omega } \right)}^{2}}}=A+\Delta {{l}_{0}}-\Delta l=9,6cm\]
- Đáp án D
Câu 3: (THPT Thanh Hóa) Một con lắc lò xo đặt nằm ngang, vật có khối lượng m dao động điều hòa với biên độ A. Khi vật đến vị trí có thế năng bằng 3 lần động năng thì một vật nhỏ khác có cùng khối lượng m rơi thẳng đứng và dính chặt vào m. Khi đó hai vật tiếp tục dao động điều hòa với biên độ
A. \[\frac{\sqrt{5}}{4}A\] B. \[\frac{\sqrt{14}}{4}A\] C. \[\frac{\sqrt{7}}{2}A\] D. \[\frac{\sqrt{5}}{2\sqrt{2}}A\]
Hướng dẫn
Cơ năng của con lắc \[E={{E}_{d}}+{{E}_{t}}\], kết hợp với giả thuyết \[{{E}_{t}}={{E}_{d}}\Rightarrow x=\pm \frac{\sqrt{3}}{2}A\]
Tại vị trí này vật có tốc độ \[v=\frac{\omega A}{2}\]
Sau va chạm con lắc mới tiếp tục dao động điều hòa với tần số góc \[{\omega }'=\sqrt{\frac{k}{m+m}}=\frac{\omega }{\sqrt{2}}\]
Quá trình va chạm động lượng theo phương nằm ngang của hệ được bào toàn
\[mv=\left( m+m \right){{V}_{0}}\Rightarrow {{V}_{0}}=\frac{v}{2}=\frac{\omega A}{4}\]
Biên dộ dao động mới của con lắc \[{A}'=\sqrt{{{\left( \frac{\sqrt{3}}{2}A \right)}^{2}}+\left( \frac{{{V}_{0}}}{{{\omega }'}} \right)}=\frac{\sqrt{14}}{4}A\]
- Đáp án B
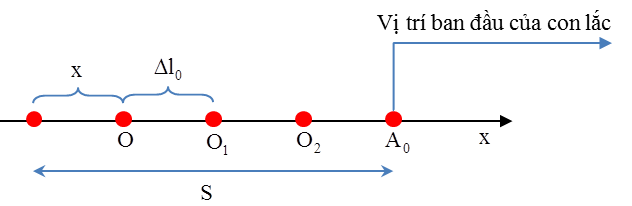
Câu 4: (Sở Nam Định – 2017) Một con lắc lò xo đặt trên mặt phẳng ngang gồm lò xo nhẹ có một đầu cố định, đầu kia gắn với vật nhỏ mang điện tích q. Chu kì dao động của con lắc là 2 s. Ban đầu vật được giữ ở vị trí lò xo bị giãn rồi thả nhẹ cho vật dao động thì thấy khi đi được quãng đường S vật có tốc độ là \[6\pi \sqrt{2}\]cm/s. Ngay khi vật trở lại vị trí ban đầu, người ta đặt một điện trường đều vào không gian xung quanh con lắc. Điện trường có phương song song với trục lò xo, có chiều hướng từ đầu cố định của lò xo đến vật, có cường độ lúc đầu là E V/m và cứ sau 2 s thì cường độ điện trường lại tăng thêm E V/m. Biết sau 4 s kể từ khi có điện trường vật đột nhiên ngừng dao động một lúc rồi mới lại dao động tiếp và trong 4 s đó vật đi được quãng đường 3S. Bỏ qua mọi ma sát, điểm nối vật, lò xo và mặt phẳng ngang cách điện. Hỏi S gần giá trị nào nhất sau đây?
A. 12,2 cm B. 10,5 cm C. 9,4 cm D. 6,1 cm
Hướng dẫn
|
|
\[\Delta {{l}_{0}}\] là độ biến dạng của lò xo ứng với cường độ điện trường có độ lớn E
Cứ lần điện trường tăng lên một lượng E thì vị trí cân bằng của con lắc dịch chuyển về phía phải một đoạn ∆l0 và biên độ sẽ giảm đi một lượng cũng đúng bằng \[\Delta {{l}_{0}}\].Trong 4 s khi đó vị trí cân bằng của con lắc bây giờ trùng với vị trí ban đầu do đó con lắc sẽ dừng lại không dao động nữa
Ta có
.png)
Kết hợp với
\[{{\left( \frac{x}{{{A}_{0}}} \right)}^{2}}+{{\left( \frac{v}{\omega {{A}_{0}}} \right)}^{2}}=1\Rightarrow {{A}_{0}}=9cm\Rightarrow S=12cm\]
- Đáp án A
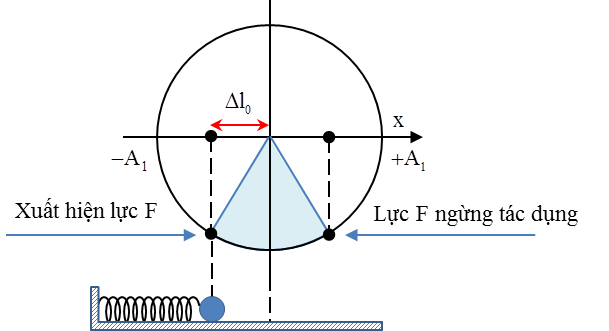
Câu 5: (Chuyên KHTN – 2017) Một con lắc lò xo nằm ngang gồm vật nặng \[m=\frac{1}{{{\pi }^{2}}}\]kg, được nối với lò xo có độ cứng \[k=100\]N/m. Đầu kia của lò xo được gắn với một điểm cố định. Từ vị trí cân bằng, đẩy vật cho lò xo nén \[2\sqrt{3}\]cm rồi buông nhẹ. Khi vật đi qua vị trí cân bằng lần đầu tiên thì tác dụng lên vật một lực F không đổi cùng chiều với vận tốc và có độ lớn \[F=2\]N, khi đó vật dao động với biên độ A1. Biết rằng lực F chỉ xuất hiện trong \[\frac{1}{30}s\] và sau khi lực F ngừng tác dụng, vật dao động điều hòa với biên độ A2. Biết trong quá trình dao động, lò xo luôn nằm trong giới hạn đàn hồi. Bỏ qua ma sát. Tỉ số \[\frac{{{A}_{1}}}{{{A}_{2}}}\] bằng
A. \[\frac{\sqrt{7}}{2}\] B. \[\frac{2}{\sqrt{7}}\] C. \[\frac{2}{\sqrt{3}}\] D. \[\frac{\sqrt{3}}{2}\]
Hướng dẫn
Chu kì dao động của con lắc \[T=2\pi \sqrt{\frac{m}{k}}=2\pi \sqrt{\frac{\frac{1}{{{\pi }^{2}}}}{100}}=0,2\text{s}\]
|
+ Dưới tác dụng của ngoại lực con lắc dao động quanh vị trí cân bằng mới, tại vị trí này lò xo giãn \[\Delta {{l}_{0}}=\frac{F}{k}=\frac{2}{100}=2cm\] \[{{A}_{1}}=\sqrt{{{\left( \Delta {{l}_{0}} \right)}^{2}}+\Delta {{l}^{2}}}=\sqrt{{{2}^{2}}+{{\left( 2\sqrt{3} \right)}^{2}}}=4\]cm + Con lắc dao động quanh vị trí cân bằng mới trong khoảng thời gian \[\Delta t=\frac{1}{30}s=\frac{T}{6}\] đến vị trí có li độ \[{{x}_{1}}=\frac{{{A}_{1}}}{2}=2cm\]và tốc độ \[{{v}_{1}}=\frac{\sqrt{3}{{v}_{1ma\text{x}}}}{2}=\frac{\sqrt{3}\omega {{A}_{1}}}{2}=\frac{\sqrt{3}10\pi .4}{2}=20\sqrt{3}\pi \]cm/s thì ngừng lực tác dụng F |
|
+ Con lắc lại dao động quanh vị trí cân bằng mới (vị trí xuất hiện lực F), với biên độ
\[{{A}_{2}}=\sqrt{{{\left( \Delta {{l}_{0}}+{{x}_{1}} \right)}^{2}}+\frac{v_{1}^{2}}{{{\omega }^{2}}}}=\sqrt{{{\left( 2+2 \right)}^{2}}+{{\left( \frac{20\sqrt{3}\pi }{10\pi } \right)}^{2}}}=2\sqrt{7}cm\]
Vậy \[\frac{{{A}_{1}}}{{{A}_{2}}}=\frac{4}{2\sqrt{7}}=\frac{2}{\sqrt{7}}\]
- Đáp án B
Câu 6: (Phan Bội Châu – 2017) Một con lắc lò xo nằm ngang gồm lò xo nhẹ không dẫn điện có độ cứng \[k=40\]N/m, qủa cầu nhỏ có khối lượng \[m=160\]g. Bỏ qua mọi ma sát, lấy \[g=10\approx {{\pi }^{2}}\]m/s2. Quả cầu tích điện \[q={{8.10}^{-5}}C\]. Hệ đang đứng yên thì người ta thiết lập một điện trường đều theo hướng dọc theo trục lò xo theo chiều giãn của lò xo, vecto cường độ điện trường với độ lớn E, có đặc điểm là cứ sau 1 s nó lại tăng đột ngột lên thành 2E, 3E, 4E… với \[E={{2.10}^{4}}\]V/m. Sau 5s kể từ lúc bắt đầu chuyển động, vật đi được quãng đường S gần nhất với giá trị nào sau đây?
A. 125 cm B. 165 cm C. 195 cm D. 245 cm
Hướng dẫn
|
|
Độ biến dạng của lò xo tại vị trí cân bằng O1
\[\Delta {{l}_{0}}=\frac{qE}{k}=\frac{{{8.10}^{-5}}{{.2.10}^{4}}}{40}=4\]cm
Chu kì dao động của con lắc \[T=2\pi \sqrt{\frac{m}{k}}=2\pi \sqrt{\frac{{{160.10}^{-3}}}{40}}=0,4\text{s}\]\[\Rightarrow \]khoảng thời gian 1 s ứng với 2,5 chu kì
+ Khi điện trường là E, vật dao động điều hòa quanh vị trí cân bằng O1. Sau khoảng thời gian \[1\text{s}=2,5T\](ứng với quãng đường đi được là 10∆l0) vật đi đến vị trí O2. Lưu ý đây là vị trí biên nên vận tốc của vật lúc này bằng 0.
+ Khi điện trường là 2E, vị trí cân bằng mới của vật là O2, do đó ở giây này con lắc đứng yên.
+ Lập luận tương tự ta sẽ thấy trong quá trìn trên con lắc chuyển động ứng với các giây thứ 1, 3 và 5 sẽ đứng yên tại giây thứ 2 và thứ 4.
Tổng quãng đường đi được \[S=30\Delta {{l}_{0}}=30.4=120cm\]
- Đáp án A
Câu 7: (Sư Phạm HN – 2017) Một lò xo lý tưởng có độ cứng \[k=100\]N/m. Một đầu gắn vào điểm I cố định, một đầu đỡ vật nặng \[M=200\]g, lấy \[g=10\]m/s2, bỏ qua mọi ma sát và sức cản, Kích thích cho vật dao động điều hòa với biên độ 3 cm quanh vị trí cân bằng theo phương thẳng đứng. Khi vật M lên tới điểm cao nhất thì người ta đặt thêm vật \[m=100\]g lên vật M. Dao động của hệ sau đó có biên độ là
A. 4 cm B. 1 cm C. 5 cm D. 3 cm
Hướng dẫn
|
+ Độ biến dạng của lò xo với con lắc M tại vị trí cân bằng của nó \[\Delta {{l}_{0}}=\frac{Mg}{k}=\frac{{{200.10}^{-3}}.10}{100}=2cm\] + Độ biến dạng của lò xo với con lắc \[M+m\] tại vị trí cân bằng của nó \[\Delta l=\frac{\left( M+m \right)g}{k}=\frac{\left( 200+100 \right){{.10}^{-3}}.10}{100}=3cm\] Biên độ dao động mới của con lắc sẽ là \[{A}'=A+\left( \Delta l-\Delta {{l}_{0}} \right)=3+\left( 3-2 \right)=4cm\]
|
|
Câu 8: (Chuyên Lê Khiết – 2017) Một con lắc lò xo được treo thẳng đứng gồm : lò xo nhẹ có độ cứng \[k=60\]N/m, một quả cầu nhỏ khối lượng \[m=150g\] và mang điện tích \[q={{6.10}^{-5}}\]C. Coi quả cầu nhỏ là hệ cô lập về điện. Lấy \[g=10\] m/s2. Đưa quả cầu nhỏ theo phương dọc trục lò xo đến vị trí lò xo không biến dạng rồi truyền cho nó một vận tốc ban đầu có độ lớn ${{v}_{0}}=\frac{\sqrt{3}}{2}\,$m/s theo phương thẳng đứng hướng xuống, con lắc dao động điều hòa. Chọn gốc thời gian là lúc quả cầu nhỏ được truyền vận tốc. Mốc thế năng tại vị trí cân bằng. Sau khoảng thời gian ngắn nhất kể từ thời điểm ban đầu quả cầu nhỏ đi qua vị trí có động năng bằng ba lần thế năng, một điện trường đều được thiết lập có hướng thẳng đứng xuống dưới và có độ lớn \[E={{2.10}^{4}}\] V/m. Sau đó, quả cầu nhỏ dao động điều hòa với biên độ bằng bao nhiêu ?
A. $\sqrt{19}\,cm$. B. $\sqrt{20}\,cm$. C. $\sqrt{21}\,cm$. D. $\sqrt{18}\,cm$
Hướng dẫn
Tần số góc của dao động
\[\omega =\sqrt{\frac{k}{m}}=\sqrt{\frac{60}{{{150.10}^{-3}}}}=20\]rad/s
Độ biến dạng của lò xo tại vị trí cân bằng \[\Delta {{l}_{0}}=\frac{mg}{k}=\frac{{{150.10}^{-3}}.10}{60}=2,5cm\]
+ Biên độ dao động ban đầu của vật
\[A=\sqrt{\Delta l_{0}^{2}+{{\left( \frac{{{v}_{0}}}{\omega } \right)}^{2}}}=\sqrt{{{2,5}^{2}}+{{\left( \frac{50\sqrt{3}}{20} \right)}^{2}}}=5\]cm
+ Vị trí động năng bằng ba lần thế năng ứng với
.png)
+ Dưới tác dung của điện trường vị trí cân bằng của con lắc sẽ dịch xuống dới một đoạn
\[\Delta l=\frac{qE}{k}=\frac{{{6.10}^{-5}}{{.2.10}^{4}}}{60}=2cm\]
Biên độ dao động mới
\[{A}'=\sqrt{{{\left( \frac{A}{2}-\Delta {{l}_{0}} \right)}^{2}}+{{\left( \frac{v}{\omega } \right)}^{2}}}\Rightarrow \sqrt{{{\left( 2,5-2 \right)}^{2}}+{{\left( \frac{50\sqrt{3}}{20} \right)}^{2}}}=\sqrt{19}cm\]
- Đáp án A
Câu 9: (Phủ Lý – 2017) Một con lắc lò xo gồm vật nặng có khối lượng 100 g và lò xo có độ cứng 40 N/m được đặt trên mặt phẳng ngang không ma sát. Vật nhỏ đang nằm yên tại vị trí cân bằng, mang điện tích \[q=40\mu C\]. Tại t = 0, có điện trường đều \[E={{5.10}^{4}}\]V/m theo phương ngang làm cho con lắc dao động điều hòa, đến thời điểm \[t=\frac{\pi }{3}s\] thì ngừng tác dụng điện trường E. Dao động của con lắc sau khi không còn chịu tác dụng của điện trường có biên độ gần nhất giá trị nào sau đây?
A. 9 cm B. 5 cm C. 7 cm D. 11 cm
Hướng dẫn
Tần số góc của dao động \[\omega =\sqrt{\frac{k}{m}}=\sqrt{\frac{40}{{{100.10}^{-3}}}}=20\]rad/s
Độ biến dạng của lò xo tại vị trí cân bằng \[\Delta {{l}_{0}}=\frac{qE}{k}=\frac{{{40.10}^{-6}}{{.5.10}^{4}}}{40}=5cm\]
Dưới tác dụng của điện trường con lắc sẽ dao động với biên độ \[A=\Delta {{l}_{0}}\]
Sau khoảng thời gian \[t=\frac{\pi }{3}s\Leftrightarrow \varphi ={{120}^{0}}\] vật đi đến vị trí
.png)
Sau khi ngắt điện trường, con lắc dao động quanh vị trí cân bằng cũ với biên độ
\[{A}'=\sqrt{{{\left( x+\Delta {{l}_{0}} \right)}^{2}}+\left( \frac{v}{\omega } \right)}=\sqrt{{{\left( 2,5+5 \right)}^{2}}+{{\left( \frac{25\sqrt{3}}{20} \right)}^{2}}}=7,81cm\]
|
|
- Đáp án C
Câu 10: (Chuyên Lam Sơn – 2017) Một vật có khối lượng \[m=150\]g treo vào một lò xo nhẹ có độ cứng \[k=100\]N/m đang đứng yên ở vị trí cân bằng thì có một vật nhỏ khối lượng \[{{m}_{0}}=100\]g bay theo phương thẳng đứng lên trên với tốc độ \[{{v}_{0}}=50\]cm/s và chạm tức thời và dính vào vật m. Lấy \[g=10\]m/s2. Biên độ của hệ sau va chạm
A. \[\sqrt{3}cm\] B. 2 cm C. 3 cm D. \[\sqrt{2}cm\]
Hướng dẫn
|
+ Độ biến dạng của lò xo tại vị trí cân bằng \[\Delta {{l}_{0}}=\frac{mg}{k}=\frac{{{150.10}^{-3}}.10}{100}=1,5cm\] + Độ biến dạng của lò xo tại vị trí cân bằng mới sau va chạm \[\Delta {{l}_{0}}=\frac{\left( m+{{m}_{0}} \right)g}{k}=\frac{\left( 150+100 \right){{.10}^{-3}}.10}{100}=2,5cm\] Tần số góc của dao động sau va chạm \[\omega =\sqrt{\frac{k}{m+{{m}_{0}}}}=20\]rad/s Vận tốc của hai vật sau va chạm \[v=\frac{{{m}_{0}}{{v}_{0}}}{m+{{m}_{0}}}=\frac{100.50}{150+100}=20\]cm/s + Biên độ dao động mới của vật \[{A}'=\sqrt{\underbrace{{{\left( \Delta l-\Delta {{l}_{0}} \right)}^{2}}}_{{{x}_{0}}}+{{\left( \frac{v}{\omega } \right)}^{2}}}=\sqrt{2}\]cm
|
|
Câu 11: (Chuyên Vinh – 2017) Một con lắc lò xo nằm ngang gồm vật nhỏ có khối lượng m = 250g và lò xo có độ cứng k =100 N/m. Bỏ qua ma sát. Ban đầu, giữ vật ở vị trí lò xo nén 1 cm. Buông nhẹ vật, đồng thời tác dụng vào vật một lực F = 3 N không đổi có hướng dọc theo trục lò xo và làm lò xo giãn. Sau khoảng thời gian \[\Delta t=\frac{\pi }{40}s\] thì ngừng tác dụng F. Vận tốc cực đại của vật sau đó bằng
A. 0,8 m/s. B. 2 m/s. C. 1, 4 m/s. D. 1 m/s.
Hướng dẫn
|
+ Tần số góc và chu kì của dao động vật sẽ dao động quanh vị trí cân bằng mới, tại vị trí này lò xo đã giãn một đoạn \[\Delta {{l}_{0}}=\frac{F}{k}=3cm\Rightarrow A=1+3=4cm\]
|
|
+ Ta lưu ý rằng lực F chỉ tồn tại trong khoảng thời gian \[\Delta t=\frac{\pi }{40}=\frac{T}{4}\Rightarrow \]vật đến vị trí cân bằng thì lực F ngừng tác dụng, tốc độ của vật khi đó là \[{{v}_{0}}=\omega A=80\]cm/s
+ Khi không còn lực F tác dụng, vật sẽ dao động quanh vị trí cân bằng cũ, vậy tại vị trí lực F ngừng tác dụng thì li độ của vật so với vị trí cân bằng cũ là \[\left\{ \begin{align}
& {{x}_{0}}=\Delta {{l}_{0}} \\
& v={{v}_{0}} \\
\end{align} \right.\Rightarrow {A}'=\sqrt{\Delta l_{0}^{2}+{{\left( \frac{{{v}_{0}}}{\omega } \right)}^{2}}}=5cm\]
Tốc độ cực đại của vật \[{{v}_{ma\text{x}}}=\omega {A}'=100\]cm/s
- Đáp án D
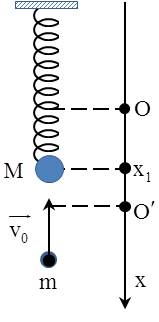


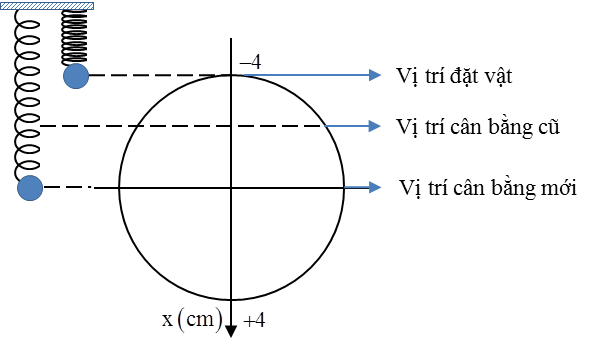
.png)