Dao Động Tắt Dần- Duy Trì-Cưỡng Bức Của Con Lắc Đơn

DAO ĐỘNG TẮT DẦN-CƯỠNG BỨC- DUY TRÌ CỦA CON LẮC ĐƠN

A: KIẾN THỨC CẦN CÓ

I. DAO ĐỘNG TẮT DẦN DƯỚI TÁC DỤNG CỦA LỰC MA SÁT

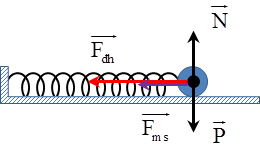
1. Con lắc lò xo nằm ngang

a. Khảo sát chuyển động của vật Chọn gốc tọa độ O là tại vị trí mà lò xo không bị biếndạng + Phương trình định luật II Niuton cho vật khi nó đang ở vị trí có li độ x và chuyển động theo chiều dương: \[\overrightarrow{N}+\overrightarrow{P}+\overrightarrow{{{F}_{ms}}}+\overrightarrow{{{F}_{dn}}}=m\overrightarrow{a}\] Theo trục Ox:\[-kx-\mu mg=m{x}''\Leftrightarrow \frac{m}{k}{x}''+\left( x+\frac{\mu mg}{k} \right)=0\] , ta đặt \[X=x+\frac{\mu mg}{k}\]\[\Rightarrow {x}''={X}''\]

Phương trình trên trở thành \[{X}''+\frac{k}{m}X=0\]\[\Rightarrow X=Ac\text{os}\left( \omega t+\varphi  \right)\] hay \[x=Ac\text{os}\left( \omega t+\varphi  \right)-\frac{\mu mg}{k}\]

Một cách tổng quát hơn, phương trình li độ của vật dao động tắt dần là:\[x=A\cos \left( \omega t+\varphi  \right)\pm \frac{\mu mg}{k}\]

Trong đó:

• \[{{x}_{2}}=A\cos \left( \omega t+\varphi  \right)-\frac{\mu mg}{k}\] ứng với trường hợp vật chuyển động theo chiều dương
• \[{{x}_{2}}=A\cos \left( \omega t+\varphi  \right)+\frac{\mu mg}{k}\]ứng với trường hợp vật chuyển động theo chiều âm

Từ phương trình trên ta có thể đi đến kết luận rằng:

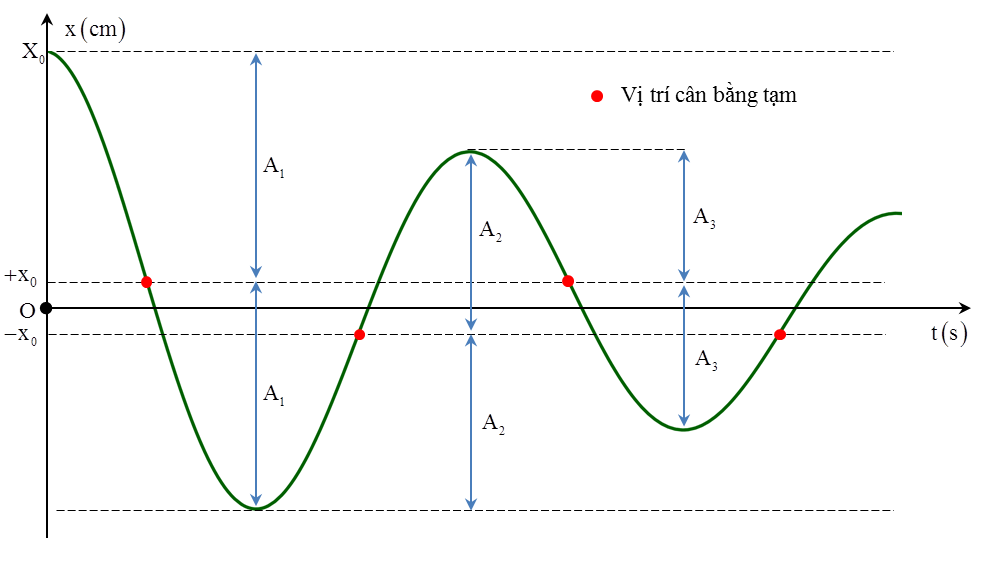
• Khi vật chuyển động theo chiều dương của trục Ox thì vị trí cân bằng của vật sẽ lệch về phía tọa độ âm một đoạn \[\frac{\mu mg}{k}\]
• Khi vật chuyển động theo chiều âm của trục Ox thì vị trí cân bằng của vật sẽ lệch về phía tọa độ dương một đoạn \[\frac{\mu mg}{k}\]

+ Vật vẫn “dao động” với chu kì \[T=\frac{2\pi }{\omega }\]

 

b. Tốc độ cực đại của con lắc trong quá trình vật dao động

+ Vật dao động tắt dần thì cơ năng của vật sẽ giảm dần theo thời gian, kết quả là vật sẽ có tốc độ lớn nhất khi nó đang di chuyển trong khoảng một phần tư chu kì thứ nhất:

Gọi x là vị trí của vật, áp dụng định luật bảo toàn cơ năng: \[\frac{1}{2}kX_{0}^{2}=\frac{1}{2}m{{v}^{2}}+\frac{1}{2}k{{x}^{2}}+\mu mg\left( {{X}_{0}}-x \right)\]

\[\Rightarrow {{v}^{2}}=\frac{k}{m}\left( A_{0}^{2}-{{x}^{2}} \right)-2\mu g\left( {{A}_{0}}-x \right)\]

Đạo hàm hai vế theo x:\[2v\frac{dv}{dx}=-\frac{2k}{m}x+2\mu g\]

Tại vị trí tốc độ của vật đạt cực đại thì \[\frac{dv}{dx}=0\Rightarrow {{x}_{0}}=\frac{\mu mg}{k}\]

Thay kết quả của x vào biểu thức của v ta thu được:\[{{v}_{\max }}=\omega \left( {{X}_{0}}-{{x}_{0}} \right)\]

Vậy trong dao động tắt dần của con lắc lò xo dưới tác dụng của lực ma sát, vật sẽ đạt tốc độ cực đại đi qua vị trí cân  bằng lần thứ nhất và tốc độ cực đại khi đó là \[\omega \left( {{X}_{0}}-{{x}_{0}} \right)\] trong đó X₀ là li độ do cách kích thích ban đầu

 

2. Con lắc đơn

a. Khảo sát chuyển động của vật

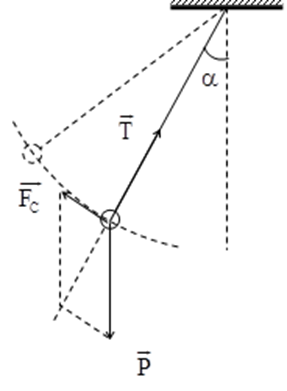
Trong quá trình dao động của con lắc, vật nặng chịu tác dụng của ba lực: + Lực căng dây \[\overrightarrow{T}\] hướng theo phương của sợi dây về điểm treo + Trọng lực \[\overrightarrow{P}\]luôn có phương thẳng đứng hướng xuống dưới + Lực cản của môi trường \[\overrightarrow{{{F}_{C}}}\]có phương tiếp tuyến với quỹ đạo, chiều ngược chiều chuyển động Phương trình định luật II Niuton cho vật trong quá trình chuyển động của con lắc: \[\overrightarrow{P}+\overrightarrow{T}+\overrightarrow{{{F}_{C}}}=m\overrightarrow{a}\] Một cách tương tự như dao động tắt dần của con lắc lò xo, trong quá trình dao động của con lắc đơn, con lắc có hai vị trí cân bằng, hai vị trí này cách gốc tọa độ O một đoạn s sao cho: \[\sin \alpha =\frac{{{F}_{C}}}{P}\] Trong trường hợp α nhỏ thì \[\sin \alpha \approx \alpha \] do vậy \[s=l\alpha =\frac{l{{F}_{C}}}{P}\]

b. Tốc độ cực đại của con lắc trong quá trình dao động:

Vật đạt tốc độ cực đại khi đi qua vị trí cân bằng lần thứ nhất

Áp dụng định luật bảo toàn cơ năng ta có: \[\frac{1}{2}mv_{\max }^{2}+\frac{1}{2}mgl{{\alpha }^{2}}=\frac{1}{2}mgl\alpha _{0}^{2}-{{F}_{C}}l\left( {{\alpha }_{0}}-\alpha  \right)\]

Với \[\alpha =\frac{{{F}_{C}}}{P}\] thay vào biểu thức trên ta thu được: \[{{v}_{\max }}=\sqrt{gl}\left( {{\alpha }_{0}}-\frac{{{F}_{C}}}{mg} \right)\]

II. DAO ĐỘNG CƯỠNG BỨC – CỘNG HƯỞNG:

1. Định nghĩa:

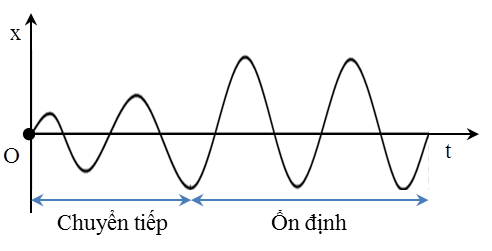
Tác dụng một ngoại lực điều hòa \[F={{F}_{0}}\cos \Omega t\] lên một vật đứng yên ở vị trí cân bằng Người ta chứng minh rằng, chuyển động của vật dưới tác dụng của ngoại lực này được chia thành hai giai đoạn + Giai đoạn chuyển tiếp: trong giai đoạn này dao động của hệ chưa ổn định, biên độ tăng dần + Giai đoạn ổn định: giai đoạn này biên độ không đổi, giai đoạn này kéo dài cho đến khi ngoại lực điều hòa ngừng tác dụng

Dao động của vật trong giai đoạn ổn định gọi là dao động cưỡng bức. Lý thuyết và thực nghiệm chứng tỏ rằng:

+ Dao động cưỡng bức là dao động điều hòa

+ Tần số của dao động cưỡng bức bằng tần số Ω của ngoại lực

+ Biên độ của dao động cưỡng bức tỉ lệ thuận với biên độ F₀ của ngoại lực và phụ thuộc vào tần số Ω của ngoại lực

2. Cộng hưởng:

Khi biên độ dao động cưỡng bức A đạt cực đại, người ta nói rằng có hiện tượng cộng hưởng

Điều kiện để xảy ra hiện tượng cộng hưởng là tần số của ngoại lực bằng tần số dao động riêng của hệ \[\Omega ={{\omega }_{0}}\]

3. Ảnh hưởng của ma sát:

Đồ thị biễu diễn  sự phụ thuộc của biên độ A của dao động cưỡng bức trong trường hợp hệ dao động và ngoại lực là giống nhau

(1) môi trường có ma sát nhớt nhỏ

(2) môi trường có ma sát nhớt lớn hơn

\[\Rightarrow \]Ma sát giảm thì giá trị cực đại của biên độ tăng, hiện tượng cộng hưởng xảy ra rõ nét hơn

 

	Dao động cưỡng bức	Dao động duy trì
Khác nhau	Tần số của dao động cưỡng bức luôn bằng tần số của ngoại lực	Tần số của ngoại lực được điều khiển để có giá trị bằng với tần số dao động riêng của hệ
Giống nhau	Đều chịu tác dụng của ngoại lực tuần hoàn theo thời gian

B: BÀI TẬP MẪU

Hướng dẫn

Vật dao động tắt dần th biên độ và năng lượng giảm dần theo thời gian

• Đáp án A

 

Hướng dẫn

Tốc độ của vật cực đại khi vật đi qua vị trí cân bằng tạm lần đầu tiên

\[{{v}_{max}}=\omega \left( {{X}_{0}}-{{x}_{0}} \right)=\sqrt{\frac{k}{m}}\left( {{X}_{0}}-\frac{\mu mg}{k} \right)=40\sqrt{2}\]cm/s

• Đáp án C

 

Hướng dẫn

Chu kì dao động của vật chính bằng chu kì dao động của ngoại lực cưỡng bức \[T=\frac{1}{f}\]

• Đáp án D

 

Hướng dẫn

Biên độ dao động của dao động cưỡng bức phụ thuộc vào độ chênh lệch giữa tần số của lực cưỡng bức và tần số dao động riêng của hệ \[{{A}_{1}}={{A}_{2}}\Leftrightarrow \left| {{f}_{1}}-{{f}_{0}} \right|=\left| {{f}_{2}}-{{f}_{0}} \right|\]

Hay \[{{f}_{1}}+{{f}_{2}}=2{{f}_{0}}\]

Từ đây ta tính được \[{{f}_{0}}=\frac{1}{2\pi }\sqrt{\frac{k}{m}}=5\Rightarrow k=100\]N/m

• Đáp án B

 

Hướng dẫn

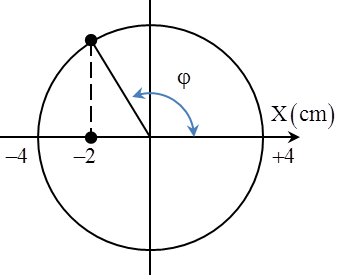
+ Biên độ dao động của vật trong quá trình chuyển động theo chiều âm lần đầu tiên \[A=\Delta l-\Delta {{l}_{0}}=4cm\] + Vị trí lực đàn hồi của lò xo nhỏ nhất là vị trí lò xo không bị biến dạng \[x=0\Leftrightarrow X=-\frac{\mu mg}{k}\] + Khoảng thời gian này ứng với góc quét \[\varphi =\frac{2\pi }{3}\] Thời gian tương ứng \[t=\frac{\varphi }{\omega }=0,296s\]

• Đáp án A

C: BÀI TẬP TỰ LUYỆN

Câu 6: Khi nói về dao động cưỡng bức phát biểu nào sau đây đúng:

          A. dao động cưỡng bức có biên độ không đổi và có tần số bằng tần số của lực cưỡng bức

          B. dao động cưỡng bức có tần số nhỏ hơn tần số của lực cưỡng bức

          C. biên độ của dao động cưỡng bức là biên độ của lực cưỡng bức

          D. dao động của con lắc đồng hồ là dao động cưỡng bức

Câu 7: Chọn câu sai:

          A. tần số của dao động cưỡng bức bằng tần số của ngoại lực tuần hoàn

          B. ngoại lực tác dụng lên quả lắc đồng hồ là trọng lực của nó

          C. quả lắc đồng hồ dao động với tần số bằng tần số riêng của nó

          D. tần số của dao động tự do là tần số riêng của nó

Câu 8: Một dao động riêng chịu tác dụng của một ngoại lực tuần hoàn để trở thành một dao động cưỡng bức. Kết luận nào sau đây sai:

          A. Lực cản môi trường càng lớn thì biên độ dao động cưỡng bức càng bé

          B. Biên độ ngoại lực càng lớn thì biên độ dao động cưỡng bức càng lớn

          C. Độ chênh lệch tần số dao động riêng với tần số ngoại lực càng lớn thì biên độ dao động càng bé

          D. Khi tần số của ngoại lực bằng với tần số dao động riêng thì biên độ dao động cưỡng bức là bé nhất

Câu 9: Phát biểu nào sau đây là sai?

A. Biên độ của dao động riêng phụ thuộc vào cách kích thích ban đầu

B. Biên độ của dao động duy trì phụ thuộc vào phần năng lượng cung cấp thêm cho dao động trong một chu kì            

C. Biên độ của dao động cưỡng bức chỉ phụ thuộc vào biên độ của ngoại lực cưỡng bức

D. Biên độ của dao động tắt dần giảm dần theo thời gian

Câu 10: Một chiếc xe chuyển động đều trên một đoạn đường mà cứ 20 m trên đường lại có một rảnh nhỏ. Biết chu kì dao động riêng của khung xe trên lò xo giảm xóc là 2 s. Chiếc xe bị xóc mạnh nhất khi tốc độ của xe là

          A. 54 km/h                   B. 36 km/h                   C. 8 km/h   D. 12 km/h

Câu 11: Một con lắc lò xo dao động điều hòa trong môi tường có lực cản. Tác dụng vào con lắc một ngoại lực cưỡng bức, tuần hoàn \[F={{F}_{0}}\cos \omega t\], tần số góc ω thay đổi được. Khi thay đổi tần số đến giá trị ω₁ và 3ω₁ thì biên độ dao động của hai con lắc đều bằng A₁. Khi tần số góc bằng 2ω₁ thì biên độ dao động của con lắc là A₂. So sánh A₁ và A₂ ta có

          A. \[{{A}_{1}}={{A}_{2}}\]                               B. \[{{A}_{1}}>{{A}_{2}}\]          C. \[{{A}_{1}}<{{A}_{2}}\]          D. \[{{A}_{1}}=2{{A}_{2}}\]

Câu 12: Một con lắc lò xo gồm vật nhỏ khối lượng 200 g và lò xo có độ cứng 20 N/m. Vật nhỏ được đặt trên giá đỡ cố định nằm ngang dọc theo trục lò xo. Hệ số ma sát trượt giữa giá đỡ và vật nhỏ là 0,01. Từ vị trí lò xo không biến dạng, truyền cho vật vận tốc ban đầu 1 m/s thì thấy con lắc dao động tắt dần trong giới hạn đàn hồi của lò xo. Lấy \[g=10\]m/s². Độ lớn của lực đàn hồi cực đại của lò xo trong quá trình dao động bằng

          A. 2 N                          B. 2,98 N                     C. 1,98 N        D. 1,5 N

Câu 13: Một con lắc lò xo đặt trên mặt phẳng nằm ngang gồm lò xo nhẹ có độ cứng 2 N/m và vật nhỏ có khối lượng 40 g. Hệ số ma sát trượt giữa vật và mặt phẳng ngang là 0,1. Ban đầu giữ vật ở vị trí lò xo bị giãn 20 cm rồi buông nhẹ để con lắc dao động tắt dần. Lấy g = 10 m/s². Kể từ lúc bắt đầu cho đến khi tốc độ của con lắc bắt đầu giảm, thế năng của con lắc lò xo đã giảm một lượng bằng

          A. 39,6 mJ                   B. 24,4 mJ                    C. 79,2 mJ      D. 240 mJ

Câu 14: Con lắc lò xo có độ cứng k = 100 N/m, khối lượng vật nặng m = 1 kg. Vật nặng đang ở vị trí cân bằng, ta tác dụng lên con lắc một ngoại lực biến đổi điều hòa theo thời gian với phương trình \[F={{F}_{0}}\cos 10\pi t\]. Sau một thời gian ta thấy vật dao động ổn định với biên độ A = 6 cm. Tốc độ cực đại của vật có giá trị bằng

          A. 60 cm/s                    B. 60π cm/s                  C. 0,6 cm/s   D. 6π cm/s

Câu 15: Con lắc lò xo gồm vật nhỏ có khối lượng 100 g và lò xo có độ cứng 10 N/m đặt trên mặt phẳng nằm ngang có hệ số ma sát giữa vật và mặt phẳng là 0,2. Đưa vật tới vị trí lò xo bị nén 10 cm rồi thả nhẹ. Ngay sau khi thả vật, nó chuyển động theo chiều dương. Tốc độ cực đại của vật trong quá trình nó chuyển động theo chiều âm lần đầu tiên là

          A. 0,80 m/s                  B. 0,40 m/s                   C. 0,70 m/s            D. 0,45 m/s 

Câu 16: Một con lắc lò xo ngang gồm lò xo có độ cứng  k =100 N/m và vật m = 100 g, dao động trên mặt phẳng ngang, hệ số ma sát giữa vật và mặt phẳng ngang là μ = 0,1 . Kéo vật lệch khỏi vị trí cân bằng một đoạn 10 cm rồi thả nhẹ cho vật dao động. Lấy g = 10 m/s². Quãng đường vật đi được từ khi bắt đầu dao động đến khi dừng hẳn là

          A. 50 m                        B. 5 m                          C. 50 cm            D. 5 cm 

Câu 17: Một con lắc lò xo đặt trên mặt phẳng ngang gồm lò xo nhẹ có độ cứng k = 50 N/m, một đầu cố định, đầu kia gắn với vật nhỏ khối lượng m₁ = 100 g. Ban đầu giữ vật m₁ tại vị trí lò xo bị nén 10 cm, đặt một vật nhỏ khác có khối lượng m₂ = 400 g sát vật m₁ rồi thả nhẹ cho hai vật bắt đầu chuyển động dọc theo phương của trục lò xo. Hệ số ma sát giữa vật và mặt phẳng nằm ngang là μ = 0,05. Lấy g = 10 m/s². Thời gian từ khi thả đến khi vật m₂ dừng lại là

          A. 2,16 s                      B. 2,21 s                      C. 2,06 s            D. 0,31 s 

Câu 18: Một con lắc lò xo đang dao động tắt dần, người ta đo được độ giảm tương đối của biên độ trong ba chu kì đầu tiên là 10%. Khi đó, độ giảm tương đối của thế năng là

          A. 10%                        B. 20%                         C. 19,5%          D. 10%

Câu 19: (Chuyên Phan Bội Châu – 2017) Một con lắc lò xo nằm ngang, lò xo có độ cứng 40 N/m, vật nhỏ có khối lượng 100 g. Hệ số ma sát giữa vật và mặt bàn là 0,2. Lấy g = 10 m/s². Ban đầu giữ cho vật sao cho bị nén 5 cm rồi thả nhẹ, con lắc dao động tắt dần. Quãng đường mà vật đi được từ lúc thả vật đến lúc gia tốc của nó đổi chiều lần thứ 3 là

          A. 18,5 cm                   B. 19,0 cm                   C. 21,0 cm      D. 12,5 cm

Bài viết gợi ý: