Bài toán đố áp dụng thực tế 1 :
Ba bạn Bảo, Vệ và Biển góp tổng cộng được 120 ngàn đồng ủng hộ các bạn học sinh ở huyện đảo Trường Sa mua tập sách nhân dịp năm học mới. Hỏi mỗi bạn đã góp bao nhiêu tiền? Biết rằng số tiền ba bạn góp theo thứ tự tỉ lệ với 2; 1; 3.
GIẢI
Gọi x, y, z (ngàn đồng) lần lượt là số tiền của bạn Bảo, Vệ và Biển ủng hộ các bạn học sinh ở huyện đảo Trường Sa mua tập sách nhân dịp năm học mới.
Theo đề bài : 3 bạn góp tổng cộng được 120 ngàn đồng, nên ta có biểu thức :
x + y + z = 120 (1)
số tiền ba bạn góp theo thứ tự tỉ lệ với 2; 1; 3 nên ta có dãy tỉ lệ thức :
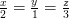(2)
Từ (1) và (2), ta có :
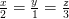và x + y + z = 120
Áp dụng tính chất của dãy tỉ lệ thức :
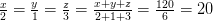
Suy ra : x = 20.2 = 40
y = 20.1 = 20
z = 20.3 = 60
vậy : bạn Bảo góp 40 ngàn đồng , Vệ góp 20 ngàn đồng và Biển góp 60 ngàn đồng.
Bài toán đố áp dụng thực tế 2 :
Trong đợt phát động phong trào “Giúp bạn đến trường”, ba lớp 7A, 7B, 7C đã góp được tất cả bao nhiêu quyển tập. Biết rằng \[\frac{1}{2}\]số tập của lớp 7A bằng \[\frac{2}{3}\]số tập của lớp 7B bằng \[\frac{3}{4}\]số tập của lớp 7C và số tập của lớp 7B ít hơn tổng số tập của 2 lớp kia là 55 tập.
GIẢI.
Gọi x, y, z (quyển) lần lượt là quyển tập của lớp 7A, 7B, 7C.
Theo đề bài : \[\frac{1}{2}\]số tập của lớp 7A bằng \[\frac{2}{3}\] số tập của lớp 7B bằng \[\frac{3}{4}\] số tập của lớp 7C. nên ta có có dãy tỉ lệ thức :
\[\frac{x}{2}=\frac{2y}{3}=\frac{3z}{4}\]
hay \[\frac{x}{12}=\frac{y}{9}=\frac{z}{8}\] (1)
số tập của lớp 7B ít hơn tổng số tập của 2 lớp kia là 55 tập. nên ta có biểu thức :
(x + z) – y = 55 hay x – y + z = 55 (2)
Từ (1) và (2), ta có :
\[\frac{x}{12}=\frac{y}{9}=\frac{z}{8}\] và x –y + z = 55
Áp dụng tính chất của dãy tỉ lệ thức :
\[\frac{x}{12}=\frac{y}{9}=\frac{z}{8}=\frac{x-y+z}{12-9+8}=\frac{55}{11}=5\]
Suy ra : x = 5.12 = 60
y = 5.9 = 45
z = 5.8 = 40
vậy : lớp 7A góp 60 quyển, 7B góp 45 quyển, 7C góp 40 quyển.
Bài toán đố áp dụng thực tế 3 :
Ba đội cày làm việc trên ba cánh đồng có diện tích như nhau. Đội thứ nhất hoàn thành công việc trong 12 ngày. Đội thứ hai hoàn thành công việc trong 9 ngày. Đội thứ ba hoàn thành công việc trong 8 ngày. Hỏi mỗi đội có bao nhiêu máy cày biết Đội thứ nhất ít hơn Đội thứ hai 2 máy và năng suất của các máy như nhau.
GIẢI.
Gọi x, y, z (máy) lần lượt là số máy của đội 1, 2, 3.
Theo đề bài : năng suất của các máy như nhau và ba cánh đồng có diện tích như nhau nên ta có có dãy tỉ lệ thức :
12x = 9y = 8x
\[\Leftrightarrow \]\[\frac{x}{6}=\frac{y}{8}=\frac{z}{9}\]
Đội thứ nhất ít hơn Đội thứ hai 2 máy. nên ta có biểu thức :
y – x = 2 \[\Leftrightarrow \] – x + y = 2
Áp dụng tính chất của dãy tỉ lệ thức :
\[\frac{x}{6}=\frac{y}{8}=\frac{z}{9}=\frac{-x+y}{-6+8}=\frac{2}{2}=1\]
Suy ra : x = 6 ; y = 8 ; z = 9
Vậy : Đội thứ nhất : 6 máy ; Đội thứ hai : 8 máy ; Đội thứ ba : 9 máy.
Bài toán đố áp dụng thực tế 4:
Nhà bạn Minh có một khu vườn trồng rau hình chữ nhật. Biết hai cạnh của khu vườn tỉ lệ với 2; 5 và chiều dài hơn chiều rộng 12m. Em hãy tính diện tích và chu vi của khu vườn đó.
GIẢI.
Gọi x, y (m) lần lượt là chiều rộng và chiều dài.
Theo đề bài : hai cạnh của khu vườn tỉ lệ với 2; 5. nên ta có có dãy tỉ lệ thức :
\[\frac{x}{2}=\frac{y}{5}\]
chiều dài hơn chiều rộng 12m nên ta có biểu thức :
y – x = 12 \[\Leftrightarrow \]– x + y = 12
Áp dụng tính chất của dãy tỉ lệ thức :
\[\frac{x}{2}=\frac{y}{5}=\frac{-x+y}{-2+5}=\frac{12}{3}=4\]
Suy ra : x = 4.2 = 8m
y = 4.5 = 20m
diện tích của khu vườn đó : 8.20 = 160 (m2).
chu vi của khu vườn đó : (8 + 20).2 = 56m.
Bài toán đố áp dụng thực tế 5 :
Có 2 xe chạy trên quãng đường AB. Xe thứ nhất chạy với vận tốc 25 km/h. Hỏi xe thứ hai chạy với vận tốc bao nhiêu ? Biết rằng để chạy hết quãng đường AB, xe thứ nhất mất thời gian bằng 1,5 thời gian xe thứ hai.
GIẢI.
Trên quãng đường AB. Gọi :
Xe thứ nhất : vận tốc v1= 25 km/h hết thời gian t1 (h)
Xe thứ hai : vận tốc v2 km/h hết thời gian t2 (h).
trên cùng quãng đường AB, ta có dãy tỉ lệ thức :
s = v1.t1 = v2.t2
hay : t1/t2 = v2/v1 (1)
Biết rằng để chạy hết quãng đường AB, xe thứ nhất mất thời gian bằng 1,5 thời gian xe thứ hai nên ta có biểu thức :
T1 = 1,5.t2
hay : t1/t2 = 1,5 (2)
từ (1) và (2) suy ra : v2/v1= 1,5
hay : v2 = 1,5 v1 = 1,5 . 25 = 37,5 km/h
vậy : xe thứ hai chạy với vận tốc 37,5 km/h.
