Bạn cần chuẩn bị đầy đủ các dạng bài toán lớp 8 cơ bản phần Đại sô để có thể đạt được số điểm cao nhất trong kỳ thi cuối kỳ cơ bản.
Bạn cần ôn luyện các dạng toán cơ bản của đại số 8 trong phần thi cuối kỳ với một số bài toán cơ bản của sách giáo khoa.
1. a) Chứng tỏ rằng thương tìm được trong phép chia (2x4 – 4x3 + 5x2 + 2x – 3) : (2x2 – 1) luôn luôn dương với mọi giá trị của x.
b) Thực hiện phép chia:
Tìm các giá trị nguyên của x để phân thức M có giá trị là một số nguyên:
M=10×2−7x−52x−3M=10×2−7x−52x−3
Lời giải chi tiết
a) Thương tìm được có thể viết:
x2−2x+3=(x2−2x+1)+2×2−2x+3=(x2−2x+1)+2
= (x−1)2+2>0(x−1)2+2>0 với mọi x
b)
M có giá trị nguyên với giá trị nguyên của x thì phải có điều kiện 72x−372x−3 là nguyên. Tức 2x – 3 là ước của 7. Hay 2x – 3 bằng ±1;±7±1;±7
+2x – 3 = 1 =>2x = 4 => x = 2
+2x – 3 = -1 => 2x = 2 => x =1
+2x – 3 = 7 => 2x = 10 => x = 5
+2x – 3 = -7 => 2x = -4 => x = -2
Vậy x ∈ {-2;1;2;5}
Vậy thương tìm được luôn luôn dương với mọi giá trị của x.
2. Phân tích các đa thức sau thành nhân tử:
a) \[{{a}^{2}}-{{b}^{2}}-4a+4;\]
b) \[{{x}^{2}}+2x-3\]
c) \[4{{x}^{2}}{{y}^{2}}-{{\left( {{x}^{2}}+{{y}^{2}} \right)}^{2}}\]
d) \[2{{a}^{3}}-54{{b}^{3}}\]
Lời giải chi tiết
a) \[{{a}^{2}}-{{b}^{2}}-4a+4\]
\[={{a}^{2}}-4a+4-{{b}^{2}}\]
\[={{(a-2)}^{2}}-{{b}^{2}}\]
\[=\left( a-2+b \right)\left( a-2-b \right)\]
\[=\left( a+b-2 \right)\left( a-b-2 \right)\]
b) \[{{x}^{2}}+2x-3={{x}^{2}}+2x+1-4\]
\[={{(x+1)}^{2}}-{{2}^{2}}\]
\[=(x+1+2)(x+1-2)\]
\[=(x+3)(x-1)\]
c) \[4{{x}^{2}}{{y}^{2}}-{{\left( {{x}^{2}}+{{y}^{2}} \right)}^{2}}\]
\[={{(2xy)}^{2}}-{{({{x}^{2}}+{{y}^{2}})}^{2}}\]
\[=(2xy-{{x}^{2}}-{{y}^{2}})(2xy+{{x}^{2}}+{{y}^{2}})\]
\[=-\left( {{x}^{2}}-2xy+{{y}^{2}} \right)\left( {{x}^{2}}+2xy+{{y}^{2}} \right)\]
\[=-{{\left( x-y \right)}^{2}}{{\left( x+y \right)}^{2}}\]
d) \[2{{a}^{3}}-54{{b}^{3}}=2\left( {{a}^{3}}-27{{b}^{3}} \right)\]
\[=2\left[ {{a}^{3}}-{{\left( 3b \right)}^{3}} \right]\]
\[=2\left( a-3b \right)\left( {{a}^{2}}+3ab+9{{b}^{2}} \right)\]
3. Chứng minh rằng hiệu các bình phương của hai số lẻ bất kì thì chia hết cho 8.
Lời giải chi tiết
Gọi hai số lẻ bất kì là 2a + 1 và 2b + 1 (a, b ∈ Z)
Hiệu bình phương của hai số lẻ đó bằng :
\[{{\left( 2a+1 \right)}^{2}}-{{\left( 2b+1 \right)}^{2}}\]
\[=\left( 4{{a}^{2}}+4a+1 \right)-\left( 4{{b}^{2}}+4b+1 \right)\]
\[=\left( 4{{a}^{2}}+4a \right)-\left( 4{{b}^{2}}+4b \right)\]
\[=4a\left( a+1 \right)-4b\left( b+1 \right)\]
Vì tích của hai số nguyên liên tiếp luôn chia hết cho 2 nên a(a+1) và b(b+1) chia hết cho 2.
Do đó 4a(a + 1) và 4b(b + 1) chia hết cho 8
4a(a + 1) – 4b(b + 1) chia hết cho 8.
Vậy \[{{\left( 2a+1 \right)}^{2}}-{{\left( 2b+1 \right)}^{2}}\] chia hết cho 8.
4. Rút gọn rồi tính giá trị của biểu thức sau tại \[x=-\frac{1}{3}\]
\[\left[ \frac{x+3}{{{\left( x-3 \right)}^{2}}}+\frac{6}{{{x}^{2}}-9}-\frac{x-3}{{{\left( x+3 \right)}^{2}}} \right].\left[ 1:\left( \frac{24{{x}^{2}}}{{{x}^{4}}-81}-\frac{12}{{{x}^{2}}+9} \right) \right]\]
Lời giải chi tiết
+ Ngoặc vuông thứ nhất:
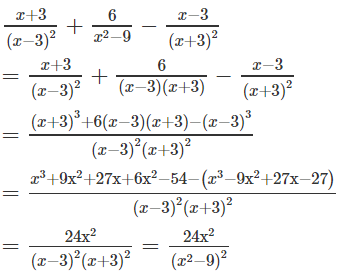
+ Ngoặc vuông thứ hai:
\[1:\left( \frac{24{{x}^{2}}}{{{x}^{4}}-81}-\frac{12}{{{x}^{2}}+9} \right)\]
\[=1:\left[ \frac{24{{x}^{2}}}{\left( {{x}^{2}}-9 \right)\left( {{x}^{2}}+9 \right)}-\frac{12}{{{x}^{2}}+9} \right]\]
\[=1:\frac{12{{x}^{2}}+108}{\left( {{x}^{2}}-9 \right)\left( {{x}^{2}}+9 \right)}\]
=\[\frac{\left( {{x}^{2}}-9 \right)\left( {{x}^{2}}+9 \right)}{12{{x}^{2}}+108}\]
\[=\frac{{{x}^{2}}-9}{12}\]
Nên \[\left[ \frac{x+3}{{{\left( x-3 \right)}^{2}}}+\frac{6}{{{x}^{2}}-9}-\frac{x-3}{{{\left( x+3 \right)}^{2}}} \right].\left[ 1:\left( \frac{24{{x}^{2}}}{{{x}^{4}}-81}-\frac{12}{{{x}^{2}}+9} \right) \right]\]\[=\frac{{{x}^{2}}-9}{12}\]







