I.Lý thuyết:
a.Định nghĩa:
Cho điểm O và góc lượng giác α, phép biến hình biến O thành chính nó, biến mỗi điểm M thành M’ sao cho: OM’ = OM và góc lượng giác (OM; OM’) = α được gọi là phép quay tâm O góc α
O: tâm α: góc quay ký hiệu: Q(O; α).
Nếu a = (2k+1)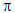
, k 
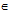Z; phép đối xứng tâm
Nếu a = 2k , k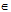 
Z; phép đồng nhất.
b. Tính chất:
+Phép quay là 1 phép dời hình nên nó có đầy đủ tính chất của phép dời hình.
+Ngoài ra; d’ = Q(O; α) (d), khi đó:
0 < α≤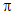 
/2 : góc giữa d và d’ bằng α
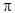/2 
: góc giữa d và d’ bằng (
- a)
+Phép quay biến:
Đường thẳng thành đoạn thẳng bằng với nó.
Tam giác thành tam giác bằng với nó.
Đường tròn thành đường tròn có cùng bán kính.
c. Biểu thức tọa độ:
Trong mặt phẳng tọa độ Oxy cho điểm M(x;y) và góc lượng giác α
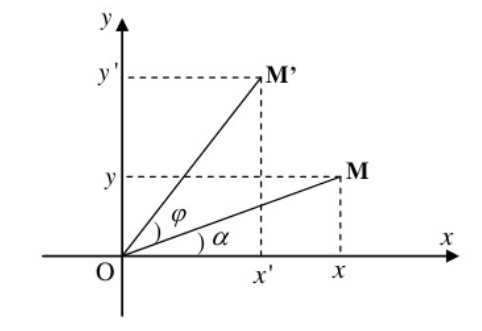
Gọi điểm M( x;y )
Đặt OM=r và góc lượng giác (Ox;OM) = α
.png)
II. Bài tập minh họa:
|
Bài 1: Trong mặt phẳng Oxy cho điểm A(1;0). Xác định tọa độ ảnh của điểm A qua phép quay tâm O góc quay bằng $\frac{\pi }{2}$. |
.png)
|
Bài 2: Trong mặt phẳng Oxy cho điểm A(1;3). Xác định tọa độ ảnh của điểm A qua phép quay tâm O góc quay bằng $\frac{\pi }{2}$. |
.png)
|
Bài 3: Trong mặt phẳng Oxy cho điểm A(2;1). Xác định tọa độ ảnh của điểm A qua phép quay tâm I(1;-2) góc quay bằng -$\frac{\pi }{2}$. |
.png)
III. Bài tập tự luyện:
Câu 1. Trong mặt phẳng Oxy cho điểm M(1; 1). Hỏi các điểm sau điểm nào là ảnh của M qua phép quay tâm O, góc 450?
A. (–1; 1) B. (1; 0) C. (\[\sqrt{2}\]; 0) D. (0; \[\sqrt{2}\])
Câu 2. Cho tam giác đều tâm O. Hỏi có bao nhiêu phép quay tâm O góc a, 0 £ a £ 2p, biến tam giác trên thành chính nó?
A. Một B. Hai C. Ba D. Bốn
Câu 3. Cho hình vuông tâm O. Hỏi có bao nhiêu phép quay tâm O góc a, 0 £ a £ 2p, biến hình vuông trên thành chính nó?
A. Một B. Hai C. Ba D. Bốn
Câu 4. Cho hình chữ nhật có O là tâm đối xứng. Hỏi có bao nhiêu phép quay tâm O góc a, 0 £ a £ 2p, biến hình chữ nhật trên thành chính nó?
A. Không có B. Hai C. Ba D. Bốn
Câu 5. Có bao nhiêu điểm biến thành chính nó qua phép quay tâm O góc a ¹ k2p, k là số nguyên?
A. Không có B. Một C. Hai D. Vô số
Câu 6. Phép quay Q(O; j) biến điểm M thành M’. Khi đó:
A. \[\overrightarrow{OM}=\overrightarrow{OM}'\] và (OM,OM’) = j B. OM = OM’ và (OM,OM’) = j
C. \[\overrightarrow{OM}=\overrightarrow{OM}'\] và MÔM’ = j D. OM = OM’ và MÔM’ = j
Câu 7. Phép quay Q(O; j) biến điểm A thành M. Khi đó:
(I) O cách đều A và M.
(II) O thuộc đường tròn đường kính AM.
(III) O nằm trên cung chứa góc j dựng trên đoạn AM.
Trong các câu trên câu đúng là:
A. Cả ba câu B. (I) và (II) C. (I) D. (I) và (III)
Câu 8. Chọn câu sai:
A. Qua phép quay Q(O; j) điểm O biến thành chính nó.
B. Phép đối xứng tâm O là phép quay tâm O, góc quay –1800
C. Phép quay tâm O góc quay 900 và phép quay tâm O góc quay –900 là hai phép quay giống nhau.
D. Phép đối xứng tâm O là phép quay tâm O, góc quay 1800
Câu 9. Trong mặt phẳng Oxy cho điểm A(3;0). Tìm tọa độ ảnh A’ của điểm A qua phép quay \[{{Q}_{(O;\frac{\pi }{2})}}\]
A. A’(0; –3); B. A’(0; 3); C. A’(–3; 0); D. A’(2\[\sqrt{3}\]; 2\[\sqrt{3}\]).
Câu 10. Trong mặt phẳng Oxy cho điểm A(3;0). Tìm tọa độ ảnh A’ của điểm A qua phép quay \[{{Q}_{(O;-\frac{\pi }{2})}}\]
A. A’(–3; 0); B. A’(3; 0); C. A’(0; –3); D. A’(–2\[\sqrt{3}\]; 2\[\sqrt{3}\]).
Đáp án
|
1.D |
2.C |
3.D |
4.B |
5.B |
6.B |
7.D |
8.C |
9.B |
10.B |
Chúc các bạn học tốt.
