Phương pháp áp dụng bất đẳng thức để chứng minh bất đẳng thức

1. BĐT bình phương của một biểu thức

A² \[\ge \] 0 với mọi giá trị của A.

Dấu “=” xảy ra khi và chỉ khi A = 0

2. Bất đẳng thức Côsi

(Cauchy là tên của Nhà toán học người Pháp 1789 – 1857)

+ Cho hai số a và b không âm , ta luôn có: \[\frac{a+b}{2}\ge \sqrt{ab}\]

Dấu “=” xảy ra khi và chỉ khi a = b

+ Cho ba số a, b, c không âm , ta luôn có: \[\frac{a+b+c}{3}\ge \sqrt[3]{abc}\]

Dấu “=” xảy ra khi và chỉ khi a = b = c

+ Tổng quát:

Cho n số a₁, a₂ ,…, a_n không âm, ta luôn có: \[\frac{{{a}_{1}}+{{a}_{2}}+...+{{a}_{n}}}{n}\ge \sqrt[n]{{{a}_{1}}{{a}_{2}}...{{a}_{n}}}\]

Dấu “=” xảy ra khi và chỉ khi a₁ = a₂ = …=a_n

(Trung bình cộng của n số không âm không nhỏ hơn trung bình nhân của chúng)

3. Bất đẳng thức Bunhiacốpxki

(Bunhiacôpxki là tên của Nhà toán học người Nga 1804 – 1889)

+ Cho các số a₁,a₂; b₁, b₂ ta có: (a₁b₁ + a₂.b₂)² \[\le \] (a₁² + a₂²) (b₁² + b₂²)

Dấu “=” xảy ra khi và chỉ khi

+ Tổng quát: Cho hai bộ số (a₁, a₂,…a_n) và (b₁, b₂, …b_n) ta luôn có :

\[{{({{a}_{1}}{{b}_{1}}+{{a}_{2}}{{b}_{2}}+...+{{a}_{n}}{{b}_{n}})}^{2}}\le ({{a}_{1}}^{2}+{{a}_{2}}^{2}+...+{{a}_{n}}^{2})({{b}_{1}}^{2}+{{b}_{2}}^{2}+...+{{b}_{n}}^{2})\]

Dấu “=” xảy ra khi và chỉ khi: \[\frac{{{a}_{1}}}{{{b}_{1}}}=\frac{{{a}_{2}}}{{{b}_{2}}}=...=\frac{{{a}_{n}}}{{{b}_{n}}}\]

(Bình phương của tổng các tích không lớn hơn tích của tổng các bình phương)

3. BĐT tổng nghịch đảo của hai số cùng dấu

Với hai số cùng dấu a và b ta có: ab+ba \[\ge \] 2. Dấu “=” xảy ra khi và chỉ khi a = b

* BĐT. với a và b là hai số dương.

Dấu “=” xảy ra khi và chỉ khi a = b

* Ngoài ra: BĐT \[\frac{1}{a}+\frac{1}{b}\ge \frac{4}{a+b}\] với a và b là hai số dương

Dấu “=” xảy ra khi và chỉ khi a = b

Với việc áp dụng các bất đẳng thức trên, Để chứng minh A > B ta tiến hành như sau:

– Từ BĐT đã biết C > D ta đi biến đổi C > D \[\Rightarrow \]…..\[\Rightarrow \] A > B rồi trả lời.

các em xem những ví dụ dưới đây để hiểu rõ hơn về cách sử dụng các bất đẳng thức đã biết ở trên để chứng minh bất đẳng thức.

Ví dụ 1: Cho a,b,c là ba số dương: Chứng minh rằng: \[\frac{a}{bc}+\frac{b}{ca}+\frac{c}{ab}\ge \frac{1}{a}+\frac{1}{b}+\frac{1}{c}\]

Giải:

Cách 1: Theo BĐT cô si: với x, y không âm ta có: \[\frac{x+y}{2}\ge \sqrt{xy}\]

Ta có: \[\frac{a}{bc}+\frac{b}{ca}\]\[\ge 2\sqrt{\frac{a}{bc}.\frac{b}{ca}}=\frac{2}{c}\]

\[\frac{b}{ca}+\frac{c}{ab}\]\[\ge 2\sqrt{\frac{b}{ca}.\frac{c}{ab}}=\frac{2}{a}\]

\[\frac{a}{bc}\]+\[\frac{c}{ab}\]\[\ge 2\sqrt{\frac{a}{bc}.\frac{c}{ab}}=\frac{2}{b}\]

Suy ra: \[2\left( \frac{a}{bc}+\frac{b}{ca}+\frac{c}{ab} \right)\ge 2\left( \frac{1}{a}+\frac{1}{b}+\frac{1}{c} \right)\]

Vậy \[\frac{a}{bc}+\frac{b}{ca}+\frac{c}{ab}\ge \frac{1}{a}+\frac{1}{b}+\frac{1}{c}\]. Dấu “=” xảy ra khi và chỉ khi a = b = c

Cách 2:

Theo BĐT tổng hai nghịch đảo ta có:

Với hai số cùng dấu a và b ta có: \[\frac{a}{b}+\frac{b}{a}\ge 2\]

Do đó : \[\frac{a}{bc}+\frac{b}{ca}=\frac{1}{c}(\frac{a}{b}+\frac{b}{a})\ge \frac{2}{c}\]

\[\frac{b}{ca}+\frac{c}{ab}=\frac{1}{a}(\frac{b}{c}+\frac{c}{b})\ge \frac{2}{a}\]

\[\frac{a}{bc}+\frac{c}{ab}=\frac{1}{b}(\frac{a}{c}+\frac{c}{a})\ge \frac{2}{b}\]

Suy ra : \[2\left( \frac{a}{bc}+\frac{b}{ca}+\frac{c}{ab} \right)\ge 2\left( \frac{1}{a}+\frac{1}{b}+\frac{1}{c} \right)\]

Vậy \[\frac{a}{bc}+\frac{b}{ca}+\frac{c}{ab}\ge \frac{1}{a}+\frac{1}{b}+\frac{1}{c}\]. Dấu “=” xảy ra khi và chỉ khi a = b = c

Ví dụ 2 : Cho hai số a và b thỏa mãn 2a+b=1. Chứng minh rằng \[2{{a}^{2}}+{{b}^{2}}\ge \frac{1}{3}\]

Giải:

Theo BĐT bunhia copxki

Với các số a₁,a₂, b₁,b₂ ta có: (a₁b₁ + a₂b₂)² \[\le \] ( a₁² + a₂²)(b₁²+ b₂²)

Dấu ‘=’ xảy ra khi và chỉ khi \[\frac{{{a}_{1}}}{{{b}_{1}}}=\frac{{{a}_{2}}}{{{b}_{2}}}\]

Ta có: 1² = (2a + b)² = (\[\sqrt{2},\sqrt{2}a+1.b{{)}^{2}}\le \left( {{\left( \sqrt{2} \right)}^{2}}+{{1}^{2}} \right)\left( {{\left( \sqrt{2}a \right)}^{2}}+{{b}^{2}} \right)\]

\[\Leftrightarrow 3(2{{a}^{2}}+{{b}^{2}})\ge 1\]

\[\Leftrightarrow 2{{a}^{2}}+{{b}^{2}}\ge \frac{1}{3}\] (dpcm)

Dấu “ = “ xảy ra khi và chỉ khi 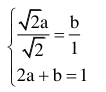\[\Leftrightarrow a=b=\frac{1}{3}\]