LÝ THUYẾT
Quan hệ giữa góc và cạnh đối diện trong một tam giác
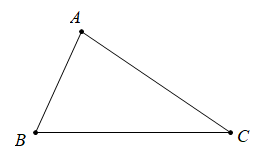
Định lí 1: Trong một tam giác, góc đối diện với cạnh lớn hơn là góc lớn hơn
$\Delta ABC,$ $AC>AB\Rightarrow \widehat{B}>\widehat{C}$
Định lí 2: Trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn.
$\Delta ABC,$ $\widehat{B}>\widehat{C}\Rightarrow AC>AB$
Quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu
Quan hệ giữa đường vuông góc và đường xiên
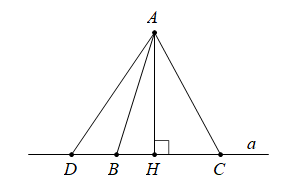
Định lí 1: Trong các đường vuông góc và đường xiên kẻ từ một điểm nằm ngoài một đường thẳng đến đường thẳng đó, đường vuông góc ngắn hơn mọi đường xiên
$AH \bot a \Rightarrow AH < AC , AH < AD$
Quan hệ giữa đường xiên và hình chiếu
Định lí 2: Trong hai đường xiên kẻ từ một điểm nằm ngoài một đường thẳng đến đường thẳng đó:
Đường xiên nào có hình chiếu lớn hơn thì lớn hơn
$AH\bot a,HD>HC\Rightarrow AD>AC$
Đường xiên nào lớn hơn thì có hình chiếu lớn hơn
$AH\bot a,AD>AC\Rightarrow HD>HC$
Nếu hai đường xiên bằng nhau thì hai hình chiếu bằng nhau; nếu hai hình chiếu bằng nhau thì hai đường xiên bằng nhau.
$AB=AC\Leftrightarrow HB=HC$
Quan hệ giữa ba cạnh của một tam giác. Bất đẳng thức tam giác
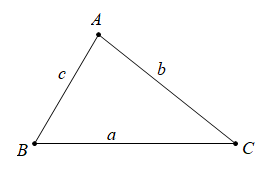
Trong một tam giác, độ dài của một cạnh bao giờ cũng lớn hơn hiệu và nhỏ hơn tổng các độ dài của hai cạnh kia.
$ \left| b-c \right| < a < b+c $
Tính chất ba đường trung tuyến của tam giác
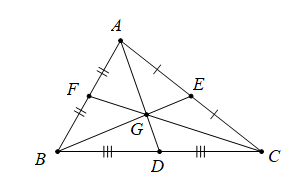
Ba đường trung tuyến của một tam giác cùng đi qua một điểm. Điểm gặp nhau của ba đường trung tuyến gọi là trọng tâm của tam giác đó.
Vị trí trọng tâm: Trọng tâm của một tam giác cách mỗi đỉnh một khoảng bằng $\frac{2}{3}$ độ dài đường trung tuyến đi qua đỉnh ấy.
G là trọng tâm của $\Delta ABC:$
$AG=\frac{2}{3}AD;$ $BG=\frac{2}{3}BE;$ $CG=\frac{2}{3}CF.$
Tính chất tia phân giác của một góc
.png)
Định lí 1: Điểm nằm trên tia phân giác của một góc thì cách đều hai cạnh của góc đó
.png)
Đinh lí 2: Điềm nằm bên trong một góc và cách đều hai cạnh của góc thì nằm trên tia phân giác của góc đó.
Tập hợp các điểm nằm bên trong một góc và cách đều hai cạnh của góc là tia phân giác của góc đó.
Tính chất ba đường phân giác của tam giác
Định lí 1: Trong một tam giác cân, đường phân giác của góc ở đỉnh đồng thời là đường trung tuyến của tam giác đó.
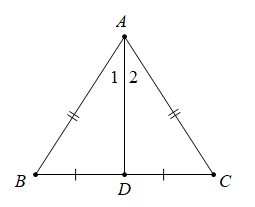
.png)
Định lí 2: Ba đường phân giác của một tam giác cùng đi qua một điểm. Điểm này cách đều ba cạnh của tam giác đó
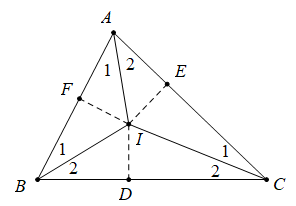
.png)
Tính chất đường trung trực của một đoạn thẳng
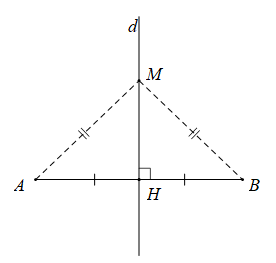
Định nghĩa: Đường trung trực của mọt đoạn thẳng là đường thẳng vuông góc với đoạn thẳng ấy tại trung điểm của nó.
Trên hình vẽ bên, d là đường trung trực của đoạn thẳng AB. Ta cũng nói: A đối xứng với B qua d.
Định lí 1: Điểm nằm trên đường trung trực của một đoạn thẳng thì cách đều hai mút của đoạn thẳng đó.
Định lí 2: Điểm cách đều hai mút của đoạn thẳng thì nằm trên đường trung trực của đoạn thẳng đó.
MA = MB $\Rightarrow $ M thuộc đường trung trực của AB.
Tập hợp các điểm cách đều hai mút của một đoạn thẳng là đường trung trực của đoạn thẳng đó.
Tính chất ba đường trung trực của tam giác
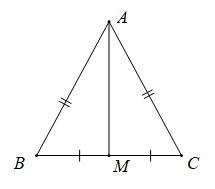
Định lí 1: Trong một tam giác cân, đường trung trực của cạnh đáy đồng thời là đường trung tuyến ứng với cạnh đáy này.
Định lí 2: Ba đường trung trực của một tam giác cùng đi qua một điểm. Điểm này cách đều ba đỉnh của tam giác đó.
Trên hình bên, điểm O là giao điểm các đường trung trực của $\Delta ABC.$ Ta có $OA=OB=OC.$ Điểm O là tâm đường tròn ngoại tiếp $\Delta ABC.$
.png)
Tính chất ba đường cao của tam giác
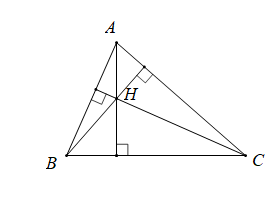
Định lí 1: Ba đường cao của một tam giác cùng đi qua một điểm. Điểm đó gọi là trực tâm của tam giác.
Trên hình bên, H là trực tâm của $\Delta ABC.$
Định lí 2: Trong một tam giác cân, đường cao ứng với cạnh đáy đồng thời là đường phân giác, đường trung tuyến, đường trung trực của tam giác đó.
Nhận xét: Trong một tam giác, nếu có hai trong bốn loại đường (đường trung tuyến, đường phân giác, đường trung trực, đường cao) trùng nhau thì tam giác đó là tam giác cân.







