Nghiệm của đa thức một biến

I.Lý thuyết:

1. Nghiệm của đa thức một biến

Cho đa thức P(x)

Nếu tại x = a đa thức P(x) có giá trị bằng 0 thì ta nói a là một nghiệm của đa thức P(x).

2. Số nghiệm của đa thức một biến

Một đa thức (khác đa thức không) có thể có 1, 2, 3, ..., n nghiệm hoặc không có nghiệm nào.

Tổng quát: Số nghiệm của một đa thức (khác đa thức 0) không vượt qua bậc của nó.

II. Bài tập vận dụng:

Bài 1: x = -2; x = 0 và x = 2 có phải là các nghiệm của đa thức x³ – 4x hay không? Vì sao?

Lời giải

Giá trị của đa thức x³ – 4x tại x = -2 là: (-2)³ – 4.( - 2) = – 8 + 8 = 0

Giá trị của đa thức x³ – 4x tại x = 0 là: 0³ – 4.0 = 0 – 0 = 0

Giá trị của đa thức x³ – 4x tại x = 2 là: 2³ – 4.2 = 8 – 8 = 0

Vậy x = -2; x = 0 và x = 2 có phải là các nghiệm của đa thức x³ – 4x

(vì tại các giá trị đó của biến, đa thức có giá trị bằng 0)

Bài 2: Kiểm tra xem:

b) Mỗi số x = 1; x = 3 có phải là một nghiệm của đa thức Q(x) = x² – 4x + 3 không.

Lời giải:

b) Ta có: Q(1) = 1² – 4.1 + 3 = 1 – 4 + 3 = 0

=> x = 1 là nghiệm của Q(x)

Q(3) = 3² – 4.3 + 3 = 9 – 12 + 3 = 0

=> x = 3 là nghiệm của Q(x)

Bài 3:

a) Tìm nghiệm của đa thức P(y) = 3y + 6.

b) Chứng tỏ rằng đa thức sau không có nghiệm: Q(x) = y⁴ + 2

Lời giải:

a) Ta có: P(x) = 3y + 6 có nghiệm khi:

    3y + 6 = 0

    3y = –6

     y = –2

Vậy đa thức P(y) có nghiệm là y = –2.

b) Ta có: y⁴ ≥ 0 với mọi y.

Nên y⁴ + 2 > 0 với mọi y.

Tức là Q(y) ≠ 0 với mọi y.

Vậy Q(y) không có nghiệm. (đpcm)

(Giải thích: y⁴ có số mũ là số chẵn nên nó luôn có giá trị lớn hơn hoặc bằng 0. Kể cả khi bạn thay y bằng số âm vào. Ví dụ, thay y = -2 chẳng hạn thì y⁴ = (-2)⁴ = 16 là số dương.)

Bài 4: Cho đa thức f(x) = x² – 4x – 5. Chứng tỏ rằng x = -1; x = 5 là hai nghiệm của đa thức đó.

Lời giải:

Thay x = -1; x = 5 vào đa thức f(x) = x² – 4x – 5, ta có:

f(-1) = (-1)² – 4.(-1) – 5 = 1 + 4 – 5 = 0

f(5) = 5² – 4.5 – 5 = 25 – 20 – 5 = 0

Vậy x = -1 và x = 5 là các nghiệm của đa thức f(x) = x² – 4x – 5

Bài 5: Tìm nghiệm của các đa thức sau:

a, 2x + 10

b, 3x - 1/2

c, x² – x

Lời giải:

a, Ta có: 2x + 10 = 0 ⇔ 2x = -10 ⇔ x = -10 : 2 ⇔ x = -5

Vậy x = -5 là nghiệm của đa thức 2x + 10

b, Ta có: 3x - 1/2 = 0 ⇔ 3x = 1/2 ⇔ x = 1/2 : 3 = 1/6

Vậy x = 1/6 là nghiệm của đa thức 3x - 1/2

c, Ta có: x² – x = 0 ⇔ x(x – 1) = 0 ⇔ x = 0 hoặc x – 1 = 0

⇔ x = 0 hoặc x = 1

Vậy x = 0 và x = 1 là các nghiệm của đa thức x² – x

III. Bài tập tự luyện:

Bài 1: Tìm nghiệm của các đa thức sau:

a. (x – 2)(x + 2)

b. (x – 1)(x² + 1)

Bài 2: Chứng tỏ rằng nếu a + b + c = 0 thì x = 1 là một nghiệm của đa thức ax² + bx + c.

Bài 3: Chứng tỏ rằng nếu a – b + c = 0 thì x = -1 là một nghiệm của đa thức ax² + bx + c

Bài 4: Chứng tỏ rằng đa thức x² + 2x + 2 không có nghiệm

Bài 5: Đố em tìm được số mà:

a. Bình phương của nó bằng chính nó

b. Lập phương của nó bằng chính nó

Bài 6: Trong các số cho sau, với mỗi đa thức, số nào là nghiệm của đa thức?

\[a)P(x)=2x+\frac{1}{2}\]	\[\frac{1}{4}\]	\[\frac{1}{2}\]	\[\frac{-1}{4}\]
b) Q(x) = x2 – 2x -3	3	1	-1

 

Bài 7: Cho đa thức:

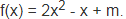
Tìm m sao cho x = -1 là một nghiệm của đa thức.

 

Bài 8: Chứng tỏ rằng nếu a = b + 1 thì x = -1 là nghiệm của đa thức:

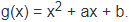
Bài 9: Tìm nghiệm của đa thức  5x + 17 – (2x + 5).

Bài 10: Tìm nghiệm của đa thức 3(1 – x) – (5 – 2x).

Chúc các bạn học tốt.

 

Bài viết gợi ý: