Câu 1:
Cho A = \[\frac{-4a{{x}^{2}}{{y}^{5}}}{{{(b+1)}^{3}}}\]
\[\]Trong các trường hợp nào A là đơn thức? trong trường hợp đó cho biết hệ số bậc của đơn thức ?
a/ a;b là hằng số b/ a là hằng số ? c/ b là hằng số ?
Câu 2:
Cho biết (x - 1) . f(x) = ( x+4 ) . f(x+8) .
Chứng minh rằng f(x) có ít nhất 2 nghiệm ?
Câu 3:
Cho đa thức P(x) = a x3 + bx2 + cx + d ( a khác 0)
Biết P(1) = 100 , P( -1) = 50 , P(0) = 1 , P( 2) = 120 . Tính P(3)
Câu 4:
Cho
\[f(x)=a{{x}^{2}}+bx+c\]
với a, b, c là các số hữu tỉ.
Chứng tỏ rằng:
\[f(-2).f(3)\le 0\]
. Biết rằng
\[13a+b+2c=0\]
Câu 5:
Cho đa thức
\[f(x)=a{{x}^{2}}+bx+c\]
với a, b, c là các số thực. Biết rằng f(0); f(1); f(2) có giá trị nguyên. Chứng minh rằng 2a, 2b có giá trị nguyên.
Câu 6:
Chứng minh rằng: f(x)
\[=a{{x}^{3}}+b{{x}^{2}}+cx+d\]
có giá trị nguyên với mọi x nguyên khi và chỉ khi 6a, 2b, a + b + c và d là số nguyên
Câu 7:
Tìm tổng các hệ số của đa thức nhận được sau khi bỏ dấu ngoặc trong biểu thức: A(x) =
\[{{(3-4x+{{x}^{2}})}^{2004}}.\ {{(3+4x+{{x}^{2}})}^{2005}}\]
Câu 8:
Cho x = 2011. Tính giá trị của biểu thức:
\[{{x}^{2011}}-2012{{x}^{2010}}+2012{{x}^{2009}}-2012{{x}^{2008}}+....-2012{{x}^{2}}+2012x-1\]
Câu 9:
Cho đa thức f(x) =ax3+bx2+cx+d. Với f(0) và f(1) là các số lẻ. Chứng minh rằng f(x) không có nghiệm là số nguyên
Câu 10:
chứng minh hằng đẳng thức
A=(x-a)(x-b)+(x-b)(x-c)+(x-c)(x-a)=ab+bc+ca-x2
Biết rằng 2x=a+b+c
Câu 11:
Rút gọn biểu thức:
A=(a+b+c)(a2+b2+c2-ab-bc-ca)
Câu 12:
Chứng minh hằng đẳng thức:
A= (100+a)(100+b)=(100+a+b).100+ab
Từ đó suy ra quy tắc nhân nhẩm hai số lớn hơn 100
Câu 13:
Cho các đơn thức: -5x2y3 ; 3xy2z ; 23x2y3 ; 10x2y2z ; - 14xy2z3 ; 35
x2y2z ; 4x2y3 ; xy2z3
- Hãy sắp xếp các đơn thức sau thành đơn thức đồng dạng
- Thu gọn bằng cách tính tổng các đơn thức đồng dạng ở các nhóm trên
Câu 14:
- Tìm số tự nhiên n sao cho n+8
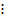n+1 - Tìm số tự nhiên n lớn nhất có hai chữ số sao cho n2-n
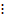5
Câu 15:
Thu gọn các phép tính sau:
- x(x+2)+y(y+3)+x2+2y2+4y
- x(x+3)+y(y-4)+y2+x2-8y
- (x+y)x +(x+y)y
- (x+y)x + (x-y)y
Lời giải chi tiết
Câu 1:
a/ Nếu a,b là hằng số thì A là đơn thức . Có hệ số
\[\frac{-4a}{{{(b+1)}^{3}}}\]
;
Bậc 2 đối với biến x. Bậc 5 đối với biến y và bậc 7 (=2+5) Đ/với tập hợp các biến.
b/ Néu chỉ có a là hằng số thì A không phải là đơn thức .Vì A có chứa phép chia phép cộng đối với biến b.
c/ Nếu b là hằng thì A là đơn thức có hệ số là
\[\frac{-4b}{(b+1)}.\]
Câu 2:
Vì (x-1).f(x) = (x+4).f(x+8) với mọi x nên suy ra :
- Khi x- 1 thì : 0.f(1)=5.f(9) => f(9) = 0
=> x=9 là một nghiệm
- Khi x=-4 thì: -5.f(-4)=0.f(4)=>f(4)= 0
=>x=-4 là một nghiệm
Vậy f(x) có ít nhất 2 nghiệm 9 và -4 .
Câu 3:
ta có P(1) = 100 $\Rightarrow$ a + b + c + d = 100
P(-1) = 50 $\Rightarrow$ - a + b – c + d = 50
P( 0) = 1 $\Rightarrow$ d = 1
P(2) = 8a + 4b + c + d = 120
Từ đó tìm được c, d, và a và XĐ được P(x)
Câu 4:
f( -2) = 4a – 2b + c và f(3) = 9a + 3b + c $\Rightarrow$ f(-2).f(3) =(4a – 2b + c)( 9a + 3b + c)
Nhận thấy ( 4a – 2b + c) + ( 9a + 3b + c) = 13a + b + 2c = 0
$\Rightarrow$ ( 4a – 2b + c ) = - ( 9a + 3b + c)
Vậy f(-2).f(3) = - ( 4a – 2b + c).( 4a – 2b + c) = - ( 4a -2b + c)2 $\le$ 0
Câu 5:
f(0) = c , f(1) = a + b + c , f(2) = 4a + 2b + c
Do f(0) ,f(1), f(2) nguyên $\Rightarrow$ c , a + b + c và 4a + 2b + c nguên
$\Rightarrow$ a + b và 4a + 2b = 2 (a + b) + 2a = 4( a + b) -2b ngyên $\Rightarrow$ 2a , 2b nguyên
Câu 6:
f(0) = d , f(1) = a + b + c + d , f(2) = 8a +4 b + c + d
Nếu f(x) có giá trị nguyên với mọi x $\Rightarrow$ d , a + b + c + d, 8a +4b + c + d là các số nguyên . Do d nguyên $\Rightarrow$ a + b + c nguyên và (a + b + c + d) + (a + b +c +) +2b nguyên $\Rightarrow$2b nguyên $\Rightarrow$ 6a nguyên . Chiều ngược lại cm tương tự.
Câu 7:
Giả sử A( x) = ao + a1x + a2x2 + …..+ a4018x4018
Khi đó A(1) = ao + a1 +a2 + …….+ a4018
do A(1) = 0 nên ao + a1 +a2 + …….+ a4018 = 0
Câu 8:
Đặt A =
\[{{x}^{2011}}-2012{{x}^{2010}}+2012{{x}^{2009}}-2012{{x}^{2008}}+....-2012{{x}^{2}}+2012x-1\]
\[{{x}^{2010}}(x-2011)-{{x}^{2009}}(x-2011)-{{x}^{2008}}(x-2011)+....-x(x-2011)+x-1\]
$\Rightarrow$ tại x = 2012 thì A = 2011
Câu 9:
Giả sử f(x) có nghiệm nguyên là n. Ta có:
F(n)= an3+bn2+cn+d=0
F(0)=d là số lẻ
F(1)=a+b+c+d là số lẻ
- Nếu n là số chẵn: suy ra an3+bn2+cn là số chẵn mà d lẻ ⇒f(n) là số lẻ. Điều này vô lí vì f(n)=0
- Nếu n là số lẻ: suy ra n3-1; n2-1; n-1 là số chẵn.
Xét f(n)-f(1)=a(n3-1)+b(n2-1)+c(n-1) là số chẵn
Nhưng f(n)-f(1)=0-f(1)=-f(1) là số lẻ, điều này vô lí
Vậy f(x) không có nghiệm nguyên
Câu 10:
Ta hãy biến đổi vế trái của biểu thức A ta được:
VT= x2-bx-ax+ab+x2-cx-bx+bc+x2-ax-cx+ac
=3x2-2x(a+b+c)++(ab+bc+ca)
Thay a+b+c=2x ta được:
VT=3x2-4x2+ab+bc+ca=-x2+ab+bc+ca (đpcm)
Câu 11:
Nhân phá ra cuối cùng ta được: A=a3+b3+c3- 3abc
Câu 12:
Chứng minh:
Ta có VT= 1002+100b+100a+ab=(100+a+b).100+ab=VP (đpcm)
Quy tắc nhân nhẩm hai số lớn hơn 100 một chút
Gọi x là số bất kì lớn hơn 100 , ta gọi hiệu x-100 là phần hơn. Muốn nhân 2 số lớn hơn 100 ta lấy số này cộng với phần hơn của số kia rồi viết tiếp vào sau tích của hai phần hơn (bằng 2 chữ số)
Ví dụ 112.103=11536(115=112+03;36=12.03)
102.106=10608 (106=102+04;08=02.04)
Câu 13:
- Các cặp đơn thức đồng dạng
+) Nhóm 1:
-5x2y3 ; 23x2y3 ; 4x2y3
+) Nhóm 2:
3xy2z3 ; - 14xy2z3 ; zy2z3
+) Nhóm 3:
10x2y2z ; 35x2y2z
- Thu gọn
+) ( -5x2y3 ) + 23
x2y3 + 4x2y3 = -5+23+4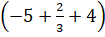
x2y3 = -15+2+43
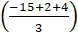x2y3 = -93
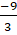x2y3
= -3x2y3
+) 3xy2z + -1 4xy2z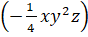
+ xy2z = 3-14+4
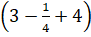xy2z = 12-1+44
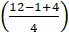xy2z = 154
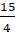xy2z3
+) 10x2y2z + 35
x2y2z = 10+35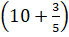
x2y2z = 505+ 35
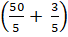x2y2z = 535
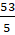x2y2z
Câu 14:
- Ta có n+8
n+1
- n+1+7
n+1 - 7
n+1 - n+1 ∈
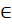1;7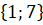
Vậy n ∈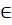
0;6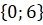
- Ta thấy n2-n = n(n-1)
5
ó n hoặc n-1 
5
Nếu n
5 => n tận cùng bằng 0 hoặc 5
Nếu n-1 
5 => n-1 tận cùng bằng 0 hoặc 5
Tức n tận cùng bằng 1 hoặc 6
Như vậy n2-n 
5 khi có n tận cùng bằng 0;1;5;6
Để n là số lớn nhất có hai chữ số ta chọn n= 96
Câu 15:
- x(x+2)+y(y+3)+x2+2y2+4y
= x2+2x +y2+3y+x2+2y2+4y
= ( x2+x2) + ( y2+2y2) + ( 3y+4y)+2x
=2x2+3y2+7y+2x
- x(x+3)+y(y-4)+y2+x2-8y
= x2+3x+y2-4y+y2+x2-8y
= ( x2+x2) + (y2+y2) + (-4y-8y) +3x
= 2x2+2y2- 12y +3x
- (x+y)x+(x+y)y
= x2+xy+xy+y2
=x2+(xy+xy)+y2
= x2+(1+1)xy +y2
= x2+2xy-y2
- (x+y)x + (x-y)y
= x2+xy+xy-y2
= x2+ (xy+xy) – y2
= x2+(1+1)xy – y2
= x2+2xy-y2
