Bất đẳng thức trong tam giác

Quan hệ giữa  ba cạnh của một tam giác. Bất đẳng thức tam giác

I . Lí thuyết :

    1 . Tính chất :

Trong một tam giác, độ dài của một cạnh bao giờ cũng lớn hơn hiệu và nhỏ hơn tổng các độ dài của hai cạnh còn lại.

   2 . Dạng toán và phương pháp giải :

          Dạng 1: Khẳng định sự tồn tại của một tam giác khi biết độ dài ba cạnh:

                 Phương pháp giải:

                 - Tồn tại một tam giác có độ dài ba cạnh là a, b, c là:

                                  

   - Trong trường hợp xác định được a là số lớn nhất trong 3 số a, b, c thì điều kiện để tồn tại tam giác chỉ cần a < b + c.

Bài toán 1: Có thể có tam giác nào mà độ dài ba cạnh như sau không?

                 a, 5cm, 10cm, 12cm.

                 b, 1m, 2m, 3m.

                 c, 6m, 9m, 8m.

                                                   Giải

           a, Ta có a = 12cm, b = 10cm, c = 5cm.

                    Theo điều kiện tồn tại , có :

                           

                    Thay các giá trị vào ta được :

                         

          Vậy tồn tại tam giác có độ dài ba cạnh là 5cm, 10cm, 12cm.

   b, Ta có a = 6m, b = 9m, c = 8m.

                    Theo điều kiện tồn tại , có :

                             

                    Thay các giá trị vào ta được :

                                

                  Vậy không tồn tại tam giác có độ dài ba cạnh là 1m, 2m, 3m.

         c, Ta có a = 12cm, b = 10cm, c = 5cm.

                    Theo điều kiện tồn tại , có :

                                 

                    Thay các giá trị vào ta được :

                                 

                   Vậy tồn tại tam giác có độ dài ba cạnh là 6m, 9m, 8m.

Dạng 2: Chứng minh các bất đẳng thức về độ dài:

           Phương pháp giải: Sử dụng bất đẳng thức về tam giác và các biến đổi về bất đẳng thức.

- Cộng cùng một số vào hai vế của bất đẳng thức:

                     

- Cộng từng vế hai bất đẳng thức cùng chiều:

               

Bài toán 2: Cho tam giác ABC có M là trung điểm BC. Chứng minh : AB + AC > 2AM.

                                                                          Giải

Trên tia đối của tia MA, lấy điểm N sao cho MN = MA.

=> AN = 2AM

Xét ΔABM và ΔNCM, ta có :

MB = MC (M là trung điểm của BC)

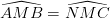 (đối đỉnh).

MA = MN (gt).

=> ΔABM = ΔNCM (c -g -c)

=>  AB = NC

Xét ΔACN, ta có :

AC + CN > AN (định lí tam giác)

mà : CN = AB (cmt) ; AN = 2AM (cmt)

vậy : AB + AC > 2AM (đpcm)

II . Bài tập :

Bài 1: Một tam giác cân có một cạnh bằng 6cm. Tính hai cạnh còn lại, biết chu vi của tam giác đó bằng 20cm.

Bài 2: Cho tam giác ABC có BC = 1cm, AC = 7 cm. Tìm độ dài cạnh AB, biết độ dài này là 1 số nguyên.

Bài 3: Tính chu vi của một tam giác cân biết độ dài hai cạnh của nó là 3,9cm và 7,9cm.

Bài 4: Có thể có tam giác nào mà độ dài ba cạnh như sau không ?

               a, 3cm, 4cm, 5cm.

               b, 2m, 2m, 5m.

               c, 5m, 10m, 15m.

Bài 5: Cho tam giác ABC có AB = 1cm, AC = 4cm, độ dài cạnh BC là một số nguyên. Tính độ dài BC.

Bài 6: Cho tam giác ABC, trên tia đối của tia AC lấy điểm K.

                a, So sánh AB với KA + KB;

                b, Chứng minh AB + AC < KB + KC.

Bài 7: Cho tam giác ABC cân tại A. TRên tia đối của tia BA lấy điểm D sao cho BD = BA. Chứng minh DC > AB.

Bài 8: Cho tam giác ABC điểm O nằm trong tam giác, Tia BO cắt cạnh AC tại I.

                a, So sánh OA và IA + IO, từ đó suy ra OA + OB <  IA + IB;

                b, Chứng minh OA + OB < CA + CB;

                c, Chứng minh OA + OB + OC < AB + BC + CA.

Bài 9: Cho tam giác ABC có AB < AC. Tia phân giác góc A cắt cạnh BC tại D, Trên cạnh AC lấy E sao cho AE = AB.

                a, So sánh DB và DE;

                b, Chứng minh AC – AB > DC – DB.

 Bài 10: Cho tam giác ABC. Gọi M là trung điểm của BC. Chứng minh: 

 

 

 

 

Bài viết gợi ý: