SỰ
BIẾN THIÊN CHU KÌ CON LẮC ĐƠN
I. LÝ THUYẾT:
1. Biến thiên nhỏ của chu kì con lắc đơn
(Các công thức
trong mục này là các công thức gần đúng, chỉ được áp dụng khi sự biến thiên của
chu kì là rất nhỏ)
-Gọi
T (T\[\equiv \]T1) là chu kì đúng (ban đầu) của con lắc đơn; T2
là chu kì sai của con lắc đơn (khi có sự ảnh hưởng bên ngoài)
·
Độ biến thiên của chu kì:
\[\Delta
T={{T}_{2}}-{{T}_{1}}={{T}_{2}}-T\]
+Ảnh hưởng của chiều dài:
\[\frac{\Delta T}{T}=\frac{\Delta l}{2l}\]
·
\[\Delta
l={{l}_{2}}-{{l}_{1}}\] là độ biến thiên chiều dài.
+Ảnh hưởng của nhiệt độ:
\[\frac{\Delta
T}{T}=\frac{1}{2}\alpha .\Delta {{t}^{o}}\]
·
\[\alpha \] là hệ số nở dài.
·
\[\Delta {{t}^{o}}={{t}_{2}}-{{t}_{1}}\] là độ biến thiên nhiệt độ.
+Ảnh hưởng của vị trí địa lý:
\[\frac{\Delta
T}{T}=\frac{\Delta g}{2g}\]
·
\[\Delta g={{g}_{2}}-{{g}_{1}}\]là độ biến thiên gia tốc trọng
trường.
+Ảnh hưởng của độ cao:
\[\frac{\Delta
T}{T}=\frac{h}{R}\]
·
\[h\]
là độ cao so với mặt đất.
·
\[R\]=6400km
là bán kính trái đất.
+Ảnh hưởng độ sâu:
\[\frac{\Delta
T}{T}=\frac{d}{2R}\]
·
\[d\]
là độ sâu so với mặt đất (\[d\ll R\]).
+Ảnh hưởng đồng thời của độ cao và nhiệt
độ:
Con lắc đơn có chu kì đúng là T ở độ
cao \[{{h}_{1}}\] và nhiệt độ \[{{t}_{1}}\].
Khi đưa tới độ cao \[{{h}_{2}}\] và nhiệt độ \[{{t}_{2}}\]thì ta có:
\[\frac{\Delta
T}{T}=\frac{\Delta h}{R}+\frac{1}{2}\alpha .\Delta {{t}^{o}}\]
· \[\Delta h={{h}_{2}}-{{h}_{1}}\] là độ biến thiên chiều cao.
+Ảnh hưởng đồng
thời của độ sâu và nhiệt độ:
Con lắc đơn có chu kì đúng là T ở độ
cao \[{{d}_{1}}\] và nhiệt độ \[{{t}_{1}}\].
Khi đưa tới độ cao \[{{d}_{2}}\] và nhiệt độ \[{{t}_{2}}\]thì ta có:
\[\frac{\Delta
T}{T}=\frac{\Delta h}{R}+\frac{1}{2}\alpha .\Delta {{t}^{o}}\]
·
\[\Delta d={{d}_{2}}-{{d}_{1}}\] là độ biến thiên độ sâu.
+Ảnh hưởng đồng
thời của độ cao và chiều dài:
\[\frac{\Delta
T}{T}=\frac{\Delta h}{R}+\frac{\Delta l}{2l}\]
+Ảnh hưởng độ
sâu và chiều dài:
\[\frac{\Delta
T}{T}=\frac{\Delta d}{2R}+\frac{\Delta l}{2l}\]
+Sự nhanh chậm
của đồng hồ quả lắc (đồng hồ đếm giây sử dụng con lắc đơn)
·
Nếu \[\Delta T>0\] (chu kì tăng): Đồng hồ chạy chậm.
·
Nếu \[\Delta T<0\] (chu kì giảm): Đồng hồ chạy nhanh.
·
Nếu \[\Delta T=0\] (chu kì không đổi): Đồng hồ chạy đúng.
Ø Thời gian đồng hồ chạy sai (nhanh hay chậm
) trong một ngày đêm (24h=86400s):
\[\Delta
t=86400.\frac{\Delta T}{T}\]
Ø
Để đồng hồ chạy đúng: (\[\Delta T=0\]) khi thay đổi đồng thời:
Độ cao và nhiệt độ: \[\frac{\Delta
h}{R}=-\frac{1}{2}\alpha .\Delta {{t}^{o}}\]
Độ cao và chiều dài: \[\frac{\Delta h}{R}=-\frac{\Delta
l}{2l}\]
Độ sâu và nhiệt độ: \[\frac{\Delta d}{R}=-\alpha
.\Delta {{t}^{o}}\]
Độ sâu và chiều dài: \[\frac{\Delta d}{R}=-\frac{\Delta
l}{l}\]
2. Biến thiên
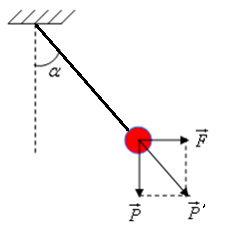
lớn của chu kì con lắc đơn: Khi con lắc đơn chịu thêm tác dụng của ngoại lực không đổi (\[\overrightarrow{F}\]):
Phương pháp giải: Khi này con lắc đơn dao động trong trường
trọng lực hiệu dụng (hay biểu kiến) có:
+Trọng lực hiệu dụng: \[\overrightarrow{{{P}'}}=\overrightarrow{P}+\overrightarrow{F}\]
+Gia tốc trọng trường hiệu dụng: \[\overrightarrow{{{g}'}}=\overrightarrow{g}+\overrightarrow{\frac{F}{m}}\]
Chu kì dao động của con lắc đơn khi đó: \[T=2\pi \sqrt{\frac{l}{{{g}'}}}\]
CÁC TRƯỜNG HỢP
ĐẶC BIỆT:
+\[\overrightarrow{F}\] có phương ngang:
·
Tại VTCB dây treo lệch với phương thẳng đứng một góc \[\alpha
\] có \[\tan \alpha =\frac{F}{P}\]
·
\[{g}'=\sqrt{{{g}^{2}}+{{a}^{2}}}\to {g}'=\frac{g}{\cos
\alpha }\to T=2\pi \sqrt{\frac{l}{{{g}'}}}={{T}_{o}}.\sqrt{\cos \alpha }\]
Với \[a=\frac{F}{m}\] là độ lớn gia tốc
do ngoại lực \[\overrightarrow{F}\] không đổi gây ra.
+\[\overrightarrow{F}\] có phương thẳng đứng:
·
Tại vị trí cân bằng dây treo vẫn có phương thẳng đứng.
·
Nếu \[\overrightarrow{F}\] hướng xuống (VD: khi thang máy đi lên nhanh dần đều hoặc đi xuống chậm dần đều với gia tốc \[\overrightarrow{a}\],…):
\[{g}'=g+a\].
·
Nếu \[\overrightarrow{F}\] hướng lên trên (VD: khi thang máy đi lên
chậm dần đều hoặc đi xuống nhanh dần đều với gia tốc \[\overrightarrow{a}\],…):
\[{g}'=g-a\].
+\[\overrightarrow{F}\] có phương hợp \[\overrightarrow{P}\] với
một góc \[\alpha \]: \[{g}'=\sqrt{{{g}^{2}}+{{a}^{2}}+2ga.cos\alpha }\].
MỘT SỐ TRƯỜNG
HỢP CỤ THỂ:
v Lực quán tính: \[\overrightarrow{F}=-m\overrightarrow{a}\]
·
Độ lớn: F=ma.
· Phương, chiều: \[\overrightarrow{F}\uparrow \downarrow \overrightarrow{a}\](cùng phương ngược chiều với gia tốc \[\overrightarrow{a}\]).
Lưu ý:
·
\[\overrightarrow{a}\uparrow \uparrow \overrightarrow{v}\] (cùng chiều chuyển động): chuyển động nhanh dần đều.
·
\[\overrightarrow{a}\uparrow \downarrow \overrightarrow{v}\] (ngược chiều chuyển động): chuyển động chậm dần đều.
Trường
hợp 1:
·
Khi thang máy đi lên nhanh
dần đều hoặc đi xuống chậm dần đều
với gia tốc \[\overrightarrow{a}\] :
→ \[\overrightarrow{F}\] hướng xuống dưới và cùng chiều với \[\overrightarrow{P}\]
→ \[{g}'=g+a\] →
\[T=2\pi \sqrt{\frac{l}{g+a}}\]
·
Khi thang máy đi lên chậm
dần đều hoặc đi xuống nhanh dần đều
với gia tốc \[\overrightarrow{a}\] :
→ \[\overrightarrow{F}\] hướng lên trên và ngược chiều với \[\overrightarrow{P}\]
→
\[{g}'=g-a\] → \[T=2\pi \sqrt{\frac{l}{g-a}}\] (với a < g)
Trường
hợp 2: Con lắc đơn treo trong toa tàu, ô tô (chuyển động thẳng trên mặt phẳng
ngang)
·
Khi toa tàu hay ô tô chuyển động nhanh dần đều hay chậm dần đều
với gia tốc \[\overrightarrow{a}\] :
→\[\overrightarrow{F}\]
hướng theo phương ngang và vuông góc với \[\overrightarrow{P}\]
→ \[{g}'=\sqrt{{{g}^{2}}+{{a}^{2}}}\] → \[T=2\pi
\sqrt{\frac{l}{\sqrt{{{g}^{2}}+{{a}^{2}}}}}\]
v
Lực điện trường: \[\overrightarrow{F}=q\overrightarrow{E}\]
·
Độ lớn: \[F=\left| q \right|E\].
·
Phương, chiều: \[\overrightarrow{F}\uparrow \downarrow
\overrightarrow{E}\] khi q<0 và khi \[\overrightarrow{F}\uparrow \uparrow
\overrightarrow{E}\] q>0.
Với q là điện tích của vật nhỏ (đơn vị:
C); là vecto cường độ điện trường (đơn vị: V/m).
Trường
hợp 1: Con lắc đơn đặt trong điện trường đều hướng thẳng đứng:
·
Khi \[\overrightarrow{E}\] hướng thẳng đứng xuống dưới (\[\overrightarrow{E}\uparrow
\uparrow \overrightarrow{P}\]):
Nếu q>0 → \[\overrightarrow{F}\uparrow \uparrow
\overrightarrow{E}\] → \[\overrightarrow{F}\uparrow \uparrow
\overrightarrow{P}\] → \[{g}'=g+\frac{\left| q \right|E}{m}\] → \[T=2\pi \sqrt{\frac{l}{g+\frac{\left| q
\right|E}{m}}}\]
Nếu q<0
→ \[\overrightarrow{F}\uparrow
\downarrow \overrightarrow{E}\] → \[\overrightarrow{F}\uparrow \downarrow
\overrightarrow{P}\] → \[{g}'=g-\frac{\left| q \right|E}{m}\] → \[T=2\pi \sqrt{\frac{l}{g-\frac{\left| q
\right|E}{m}}}\]
·
Khi \[\overrightarrow{E}\] hướng thẳng đứng lên trên (\[\overrightarrow{E}\uparrow
\downarrow \overrightarrow{P}\]):
Nếu q>0 → \[\overrightarrow{F}\uparrow \uparrow
\overrightarrow{E}\] → \[\overrightarrow{F}\uparrow \downarrow
\overrightarrow{P}\] → \[{g}'=g-\frac{\left| q \right|E}{m}\] → \[T=2\pi \sqrt{\frac{l}{g-\frac{\left| q
\right|E}{m}}}\]
Nếu q<0
→ \[\overrightarrow{F}\uparrow
\downarrow \overrightarrow{E}\] → \[\overrightarrow{F}\uparrow \uparrow
\overrightarrow{P}\] → \[{g}'=g+\frac{\left| q \right|E}{m}\] → \[T=2\pi \sqrt{\frac{l}{g+\frac{\left| q
\right|E}{m}}}\]
Trường
hợp 2: Con lắc đơn đặt trong điện trường đều nằm ngang (\[\overrightarrow{E}\bot
\overrightarrow{P}\]):
·
q>0 (hay q<0)
→ \[\overrightarrow{F}\bot
\overrightarrow{P}\] → \[{g}'=\sqrt{{{g}^{2}}+{{\left( \frac{qE}{m}
\right)}^{2}}}\] → \[T=2\pi
\sqrt{\frac{l}{\sqrt{{{g}^{2}}+{{\left( \frac{qE}{m} \right)}^{2}}}}}\]
v Lực đẩy Acsimet:
·
Độ lớn: \[F=DgV\](D là khối lượng riêng của chất lỏng hay
khí, g là gia tốc rơi tự do, V là thể tích của vật chìm trong chất lỏng hay khí
đó).
·
Phương, chiều luôn hướng thẳng đứng lên trên. Khi vật dao động
hoàn toàn trong môi trường (V là thể tích của vật):, họi Do là khối
lượng riêng của vật (Do>D) thì:
→
\[{g}'=g\left( 1-\frac{D}{{{D}_{o}}} \right)\to T=2\pi
\sqrt{\frac{l}{g\left( 1-\frac{D}{{{D}_{o}}} \right)}}\]
·
Lưu ý: Nếu D Do (ví dụ vật dao động trong không
khí) thì chu kì thay đổi nhỏ : \[\frac{\Delta T}{T}=\frac{D}{2{{D}_{o}}}\]
3. Các công thức
phổ biến:
+Nếu
\[l={{l}_{1}}+{{l}_{2}}\] → \[{{T}^{2}}={{T}_{1}}^{2}+{{T}_{2}}^{2}\].
+Nếu
\[l={{l}_{1}}-{{l}_{2}}\] → \[{{T}^{2}}={{T}_{1}}^{2}-{{T}_{2}}^{2}\].
+Chu kì, chiều dài hay gia tốc tăng giảm
theo %:
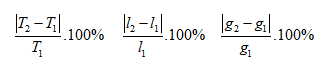
II. BÀI TẬP:
Bài 1. Một con lắc đơn có chu kỳ T=2s khi treo vào thang máy đứng yên. Khi
thang máy đi lên nhanh dần đều với gia tốc 0,1m.s-2 thì chu kỳ
dao động của con lắc là
A. 2,00s
B. 2,10s
C. 1,99s
D. 1,87s
HD: Thang máy đi lên nhanh dần đều → $\overrightarrow{a}$
hướng lên mà $\overrightarrow{F}\uparrow \downarrow \overrightarrow{a}$
Gia tốc hiệu dụng: ${g}'=g+a=10,0\left(
m/{{s}^{2}} \right)$
→${T}'=T.\sqrt{\frac{g}{{{g}'}}}=2.\sqrt{\frac{10}{10,1}}=1,99\left(
s \right)$ → Đáp án C.
Bài 2. Một con lắc đơn dao động nhỏ với chu kì T. Nếu chu kì con lắc bị giảm 1%
so với giá trị lúc ban đầu thì chiều dài của con lắc sẽ thay đổi như thế nào?
Bằng bao nhiêu phần trăm so với chiều dài ban đầu?
A. Giảm 2% B.
Tăng 2% C.
Giảm 0,2% D.Tăng 0,2%
HD: Vì chu kì tỉ lệ thuận với căn bặc hai của chiều dài nên
chu kì giảm chiều dài cũng giảm: \[\frac{\Delta
T}{T}=\frac{{T}'-T}{T}=\frac{{{T}'}}{T}-1=\frac{\Delta l}{2l}=0,01\to
\frac{\Delta l}{l}=0,02\] → Đáp án A.
Bài 3. Một con lắc đơn có chu
kì dao động T=4s tại mặt đất. Đem con lắc lên độ cao h so với mặc đất thì chu
kì dao động thay đổi 0,2% so với ban đầu. Tính độ cao h? cho bán kính Trái Đất
R=6400km.
A.
20km B. 12,8km C.10,5km D.21km
HD: 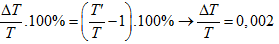
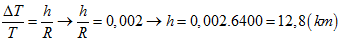
Bài 4. Một
con lắc đơn dao động bé có chu kỳ T. Đặt con lắc trong điện trường đều có
phương thẳng đứng hướng xuống dưới. Khi quả cầu của con lắc tích điện q1 thì
chu kỳ của con lắc là T1=5T. Khi quả cầu của con lắc tích điện q2 thì
chu kỳ là T2=5/7 T. Tỉ số giữa hai điện tích là
A.
q1/q2 =
-7. B.
q1/q2 = -1. C. q1/q2 =
-1/7. D. q1/q2 =
1.
HD: Lực điện trường hướng xuống, T2<><>1
Hai điện tích q1, q2 trái dấu nhau
Ta có: Fđ=ma →
qE=ma → $\frac{{{q}_{1}}}{{{q}_{2}}}=\frac{{{a}_{1}}}{{{a}_{2}}}$
* T1 = 5T (điện tích q1 âm):
$\frac{{{T}_{2}}}{T}=\frac{5}{7}=\frac{2\pi
\sqrt{\frac{l}{{{g}_{2}}}}}{2\pi
\sqrt{\frac{l}{g}}}=\sqrt{\frac{g}{{{g}_{2}}}}=\frac{g+{{a}_{2}}}{2}\to
\frac{49}{25}=\sqrt{\frac{g}{g+{{a}_{2}}}}=1+\frac{{{a}_{2}}}{g}\to
\frac{{{a}_{2}}}{g}=\frac{24}{25}$
* T2 =5/7T (điện tích q2 dương):
$$ $\frac{{{T}_{1}}}{T}=5=\frac{2\pi
\sqrt{\frac{l}{{{g}_{1}}}}}{2\pi
\sqrt{\frac{l}{g}}}=\sqrt{\frac{g}{{{g}_{1}}}}=\sqrt{\frac{g}{g-{{a}_{1}}}}\to
\frac{1}{25}=\frac{g-{{a}_{1}}}{g}=1-\frac{{{a}_{1}}}{g}\to
\frac{{{a}_{1}}}{g}=\frac{24}{25}$
Suy ra 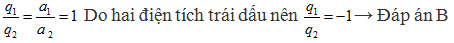
Bài 5. Con lắc đơn dao động điều hoà trong thang máy đứng yên. Khi thang
máy bắt đầu đi lên nhanh dần đều, vận tốc lúc đó của con lắc bằng 0. Cho con
lắc dao động điều hòa thì đại lượng vật lí nào không thay đổi?
A. Biên độ.
B. Chu kì.
C. Cơ năng.
D. Tần số góc.
Bài 6. Con lắc đơn dao động điều hòa trong một toa xe đứng yên với chu kì
T. chu kì dao động sẽ thay đổi khi
A. Toa xe chuyển động
thẳng đều lên cao.
B. Toa xe chuyển động
thẳng đều xuống thấp.
C. Toa xe chuyển động
thẳng đều theo phương ngang.
D. Toa xe chuyển động tròn đều trên mặt phẳng ngang.
III. TRẮC NGHIỆM:
Câu 1: Một con lắc đơn có chiều dài 0,5m treo ở trên trần một ô tô đang xuống dốc nghiêng
với phương ngang một góc 300. Lấy g = 10m/s2. Chu kì dao động điều hòa của con lắc khi ô tô xuống dốc
có hệ số ma
sát 0,2 là
A.
1,51s. B. 1,44s. C. 1,97s. D. 2,01s.
Câu 2: Một con lắc đơn được treo trên trần một thang máy. Khi thang máy
chuyển động thẳng đứng đi xuống nhanh đần đều với gia tốc có độ lớn a thì chu kì
dao động điều
hòa
của con lắc là 4s. Khi thanh máy chuyển động thẳng đứng đi xuống chậm dần đều với gia tốc có
cùng độ lớn a thì chu kì dao động điều hòa của con lắc là 2s. Khi
thang máy đứng yên thi chu kì dao động điều hòa của
con lắc là
A.
4,32s. B. 3,16s. C. 2,53s. D. 2,66s.
Câu 3: Một con lắc đơn có chu kì 2s khi treo vào thang máy đứng yên. Chu kì dao động điều hòa của
con
lắc đơn khi
thang
máy đi lên
chậm dần đều với gia tốc có độ lớn 1 m/s2 tại nơi có
g =
9,80 m/s2 bằng.
A.
4,70s. B. 1,89s. C. 1,58s. D. 2,11s.
Câu 4: Một con lắc
đơn có chu kì dao động 2s. Nếu treo con lắc
vào trần một toa xe
đang chuyển động nhanh dần đều trên mặt phẳng nằm ngang thì thấy ở vị trí cân bằng mới, dây
treo hợp với phương thẳng đứng một góc
300. Gia
tốc của toa
xe
và chu kì dao động điều
hòa
mới
của con lắc là
A.
10m/s2; 2s. B. 10m/s2; 1,86s. C. 5,55m/s2; 2s. D.5,77m/s2;1,86s.
Câu 5: Một con lắc đơn có chu kì T = 2s khi treo vào thang máy đứng yên. Chu kì của con lắc đơn dao động điều hòa khi thang máy đi lên nhanh dần đều với gia
tốc
có độ lớn 0,1 m/s2 là:
A.
1,4s. B. 1,54s. C. 1,86s. D. 2,12s.
Câu 6: Sự biến thiên tính chất của các nguyên tố thuộc chu kì sau được lặp lại tương tự như chu kì trước là do:
A. Sự lặp lại tính chất kim loại của các nguyên tố ở chu kì sau so với chu kì trước.
B. Sự lặp lại tính chất phi kim của các nguyên tố ở chu kì sau so
với chu kì trước.
C. Sự lặp lại cấu hình electron lớp ngoài cùng của
nguyên tử các nguyên tố ở chu kì sau so với chu kì trước (ở ba chu kì đầu).
D. Sự lặp lại tính chất hóa học của các nguyên tố ở chu kì sau so
với chu kì trước.







