Tam giác đồng dạng

TAM GIÁC ĐỒNG DẠNG

A. Lý thuyết

I. Định lý Talet  trong tam giác

Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ.

II. Định lý đảo và hệ quả của định lý Talet

a) Định lý Talet đảo.
Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.
b) Hệ quả của định lý Ta – let .
Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh của tam giác đã cho.

III. Tính chất đường phân giác trong tam giác

Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề của đoạn ấy.

IV. Tam giác đồng dạng

Tam giác A’B’C’ gọi là đồng dạng với tam giác  ABC nếu :
Các góc: A’ = A ; B’ = B ; C’ = C ;
Tỉ lệ các cạnh: $\frac{{{A}^{'}}{{B}^{'}}}{AB}=\frac{{{B}^{'}}{{C}^{'}}}{BC}=\frac{{{C}^{'}}{{A}^{'}}}{CA}$
– Nếu một đường thẳng cắt hai cạnh của tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới đồng dạng với tam giác đã cho.

V. Ba trường hợp đồng dạng của tam giác

1) Trường hợp thứ nhất (c.c.c)
Nếu ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia thì hai tam giác đó đồng dạng với nhau.
2) Trường hợp thứ hai (c.g.c)
Nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và hai góc tạo bởi các cặp cạnh đó bằng nhau thì hai tam giác đồng dạng với nhau.
3) Trường hợp thứ ba (g.g.g)
Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng với nhau.

VI. Các trường hợp đồng dạng của tam giác vuông

1.Áp dụng các trường hợp đồng dạng của tam giác thường vào tam giác vuông.
Hai tam giác vuông có đồng dạng với nhau nếu:
a) Tam giác vuông này có một góc nhọn bằng góc nhọn của tam giác vuông kia.
b) Tam giác vuông này có hai cạnh góc vuông tỷ lệ với hai cạnh góc vuông của tam giác vuông kia.
2.Dấu hiệu đặc biệt nhận biết 2 tam giác vuông đồng dạng:
Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này tỉ lệ với cạnh huyền và cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó đồng dạng. 
3. Tỉ số đường cao, tỉ số diện tích của hai tam giác đồng dạng
a) Tỉ số hai đường cao tương ứng của hai tam giác đồng dạng bằng tỉ số đồng dạng.
b) Tỉ số diện tích của hai tam giác đồng dạng bằng bình phương tỉ số đồng dạng.

B. Bài tập minh họa

Giải:

a. Đặt AB = c, AC = b.

BD // AC (cùng vuông góc với AB)

nên  $\frac{\text{AH}}{\text{HB}}=\frac{\text{AC}}{\text{BD}}=\frac{\text{b}}{\text{c}}\Rightarrow \frac{\text{AH}}{\text{HB}}=\frac{\text{b}}{\text{c}}\Rightarrow \frac{\text{AH}}{\text{HB + AH }}=\frac{\text{b}}{\text{b + c}}$

Hay $\frac{\text{AH}}{\text{AB }}=\frac{\text{b}}{\text{b + c}}\Rightarrow \frac{\text{AH}}{\text{c }}=\frac{\text{b}}{\text{b + c}}\Rightarrow \text{AH}=\frac{\text{b}\text{.c}}{\text{b + c}}$ (1)

AB // CF (cùng vuông góc với AC) nên   $\frac{\text{AK}}{\text{KC}}=\frac{\text{AB}}{\text{CF}}=\frac{\text{c}}{\text{b}}\Rightarrow \frac{\text{AK}}{\text{KC}}=\frac{\text{c}}{\text{b}}\Rightarrow \frac{\text{AK}}{\text{KC + AK }}=\frac{\text{c}}{\text{b + c}}$

Hay $\frac{\text{AK}}{\text{AC }}=\frac{\text{b}}{\text{b + c}}\Rightarrow \frac{\text{AK}}{\text{b }}=\frac{\text{c}}{\text{b + c}}\Rightarrow \text{AK}=\frac{\text{b}\text{.c}}{\text{b + c}}$ (2)

Từ (1) và (2) suy ra: AH = AK

b. Từ  $\frac{\text{AH}}{\text{HB}}=\frac{\text{AC}}{\text{BD}}=\frac{\text{b}}{\text{c}}$ và $\frac{\text{AK}}{\text{KC}}=\frac{\text{AB}}{\text{CF}}=\frac{\text{c}}{\text{b}}$ suy ra  $\frac{\text{AH}}{\text{HB}}=\frac{\text{KC}}{\text{AK}}\Rightarrow \frac{\text{AH}}{\text{HB}}=\frac{\text{KC}}{\text{AH}}$(Vì AH = AK)

$\Rightarrow $ AH² = BH . KC

Giải:

a) Vì ABCD là hình bình hành và K $\in $ BC nên

AD // BK, theo hệ quả của định lí Ta-lét ta có:

\[\frac{\text{EK}}{\text{AE}}\text{ = }\frac{\text{EB}}{\text{ED}}\text{ = }\frac{\text{AE}}{\text{EG}}\Rightarrow \frac{\text{EK}}{\text{AE}}=\frac{\text{AE}}{\text{EG}}\Rightarrow \text{A}{{\text{E}}^{\text{2}}}=\text{EK}\text{.EG}\]

b) Ta có: \[\frac{\text{AE}}{\text{AK}}\text{ = }\frac{\text{DE}}{\text{DB}}\] ; \[\frac{\text{AE}}{\text{AG}}\text{ = }\frac{\text{BE}}{\text{BD}}\]  nên

\[\frac{\text{AE}}{\text{AK}}+\frac{\text{AE}}{\text{AG}}\text{ = }\frac{\text{BE}}{\text{BD}}+\frac{\text{DE}}{\text{DB}}=\frac{\text{BD}}{\text{BD}}=1\Rightarrow \text{AE}\left( \frac{\text{1}}{\text{AK}}+\frac{\text{1}}{\text{AG}} \right)=1\] $\Rightarrow $ $\frac{1}{\text{AE}}=\frac{1}{\text{AK}}+\frac{1}{\text{AG}}$ (đpcm)

c) Ta có: \[\frac{\text{BK}}{\text{KC}}\text{ = }\frac{\text{AB}}{\text{CG}}\Rightarrow \frac{\text{BK}}{\text{KC}}\text{ = }\frac{\text{a}}{\text{CG}}\] (1); \[\frac{\text{KC}}{\text{AD}}\text{ = }\frac{\text{CG}}{\text{DG}}\Rightarrow \frac{\text{KC}}{\text{b}}\text{ = }\frac{\text{CG}}{\text{DG}}\] (2)

Nhân (1) với (2) vế theo vế ta có: \[\frac{\text{BK}}{\text{b}}\text{ = }\frac{\text{a}}{\text{DG}}\Rightarrow \text{BK}\text{. DG = ab}\] không đổi

(Vì a = AB; b = AD là độ dài hai cạnh của hình bình hành ABCD không đổi)

Giải:

Gọi M, N theo thứ tự là trung điểm của CF, DG

Ta có CM = $\frac{1}{2}$ CF = $\frac{1}{3}$BC $\Rightarrow $\[\frac{\text{BM}}{\text{BC}}\text{ = }\frac{1}{3}\text{ }\]$\Rightarrow $ \[\frac{\text{BE}}{\text{BA}}\text{ = }\frac{\text{BM}}{\text{BC}}\text{ = }\frac{1}{3}\text{ }\]

$\Rightarrow $EM // AC 

Tương tự, ta có: NF // BD 

mà AC = BD (3)    Từ (1), (2), (3) suy ra : EM = NF (a)

Tương tự như trên ta có: MG // BD, NH // AC và MG = NH = $\frac{1}{3}$AC (b)

Mặt khác EM // AC; MG // BD Và AC $\bot $ BD $\Rightarrow $EM $\bot $ MG $\Rightarrow $ \[\widehat{\text{EMG}}\text{ = 9}{{\text{0}}^{\text{0}}}\](4)

Tương tự, ta có:  \[\widehat{\text{FNH}}\text{ = 9}{{\text{0}}^{\text{0}}}\](5) Từ (4) và (5) suy ra  \[\widehat{\text{EMG}}\text{ = }\widehat{\text{FNH}}\text{ = 9}{{\text{0}}^{\text{0}}}\] (c)

Từ (a), (b), (c) suy ra  $\Delta $EMG = $\Delta $FNH (c.g.c) $\Rightarrow $ EG = FH

b) Gọi giao điểm của EG và FH là O; của EM và FH là P; của  EM và FN là Q thì

\[\widehat{\text{PQF}}\text{ = 9}{{\text{0}}^{\text{0}}}\]$\Rightarrow $ \[\widehat{\text{QPF}}\text{ + }\widehat{\text{QFP}}\text{ = 9}{{\text{0}}^{\text{0}}}\] mà \[\widehat{\text{QPF}}\text{ = }\widehat{\text{OPE}}\text{ }\](đối đỉnh), \[\widehat{\text{OEP}}\text{ = }\widehat{\text{QFP}}\text{ }\]($\Delta $EMG = $\Delta $FNH)

Suy ra \[\widehat{\text{EOP}}\text{ = }\widehat{\text{PQF}}\text{ = 9}{{\text{0}}^{\text{0}}}\] $\Rightarrow $ EO $\bot $ OP $\Rightarrow $ EG $\bot $ FH

Giải:

a) BD là phân giác nên

Mặt khác KD // BC nên \[\frac{\text{AD}}{\text{DC}}=\frac{\text{AK}}{\text{KB}}\] (2)

Từ (1) và (2) suy ra \[\frac{\text{AK}}{\text{KB}}<\frac{\text{AE}}{\text{EB}}\Rightarrow \frac{\text{AK + KB}}{\text{KB}}<\frac{\text{AE + EB}}{\text{EB}}\]

 nằm giữa K và B

b) Gọi M là giao điểm của DE và CB.

Ta có \[\widehat{\text{CBD}}\text{ = }\widehat{\text{KDB}}\](Góc so le trong) $\Rightarrow $\[\widehat{\text{KBD}}\text{ = }\widehat{\text{KDB}}\]

 mà E nằm giữa K và B nên \[\widehat{\text{KDB}}\] > \[\widehat{\text{EDB}}\]$\Rightarrow $\[\widehat{\text{KBD}}\] > \[\widehat{\text{EDB}}\]$\Rightarrow $ \[\widehat{\text{EBD}}\] > \[\widehat{\text{EDB}}\] $\Rightarrow $ EB < DE

Ta lại có \[\widehat{\text{CBD}}\text{ + }\widehat{\text{ECB}}\text{ = }\widehat{\text{EDB}}\text{ + }\widehat{\text{DEC}}\text{ }\]$\Rightarrow $\[\widehat{\text{DEC}}\]>\[\widehat{\text{ECB}}\] $\Rightarrow $\[\widehat{\text{DEC}}\]>\[\widehat{\text{DCE}}\] (Vì \[\widehat{\text{DCE}}\] = \[\widehat{\text{ECB}}\])

Suy ra CD > ED $\Rightarrow $ CD > ED > BE

Giải:

Cách 1: Trên tia đối của tia BA lấy điểm E sao cho:BD = BC

$\Delta $ACD  $\Delta $ABC (g.g) $\Rightarrow $ $\frac{\text{AC}}{\text{AB}}=\frac{\text{AD}}{\text{AC}}$

$\Rightarrow \text{A}{{\text{C}}^{\text{2}}}=\text{AB}\text{. AD =AB}\text{.(AB + BD)}$ = AB(AB + BC)

= 8(10 + 8) = 144 $\Rightarrow $ AC = 12 cm

Cách 2:  Vẽ tia phân giác BE của $\widehat{\text{ABC}}$$\Rightarrow $$\Delta $ABE  $\Delta $ACB

\[\frac{\text{AB}}{\text{AC}}\text{ = }\frac{\text{AE}}{\text{AB}}=\frac{\text{BE}}{\text{CB}}=\frac{\text{AE + BE}}{\text{AB + CB}}=\frac{\text{AC}}{\text{AB + CB}}\Rightarrow \text{A}{{\text{C}}^{\text{2}}}\text{ = AB(AB + CB) }\]= 8(8 + 10) = 144

 $\Rightarrow $ AC = 12 cm

b) Gọi AC = b, AB = a, BC = c thì từ câu a ta có b² = a(a + c) (1)

Vì b > anên có thể b = a + 1 hoặc b = a + 2

+ Nếu b = a + 1 thì (a + 1)² = a² + ac $\Leftrightarrow $2a + 1 = ac $\Leftrightarrow $a(c – 2) = 1

$\Rightarrow $a = 1; b = 2; c = 3(loại)

+ Nếu b = a + 2 thì  a(c – 4) = 4

- Với a = 1 thì c = 8 (loại)                     - Với a = 2 thì c = 6 (loại)

- với a = 4 thì c = 6 ; b = 5                   Vậy a = 4; b = 5; c = 6

Giải:

a) Từ \[\text{CE = }\frac{\text{O}{{\text{B}}^{\text{2}}}}{\text{BD}}\] $\Rightarrow $ \[\frac{\text{CE}}{\text{OB}}\text{ = }\frac{\text{OB}}{\text{BD}}\] và \[\widehat{\text{B}}\text{ = }\widehat{\text{C}}\text{ }\](gt) $\Rightarrow $ $\Delta $DBO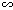$\Delta $OCE

b) Từ câu a suy ra \[{{\widehat{\text{O}}}_{\text{3}}}\text{= }{{\widehat{\text{E}}}_{\text{2}}}\] (1)

 Vì  B, O ,C thẳng hàng nên  \[{{\widehat{\text{O}}}_{\text{3}}}\text{ + }\widehat{\text{DOE}}+\widehat{\text{EOC}}={{180}^{0}}\] (2)

trong tam giác EOC thì  \[{{\widehat{\text{E}}}_{\text{2}}}\text{ + }\widehat{\text{C}}+\widehat{\text{EOC}}={{180}^{0}}\] (3)

Từ (1), (2), (3) suy ra \[\widehat{\text{DOE}}=\widehat{\text{B}}=\widehat{\text{C}}\]

$\Delta $DOE và $\Delta $DBO có \[\frac{\text{DO}}{\text{DB}}\text{ = }\frac{\text{OE}}{\text{OC}}\] (Do $\Delta $DBO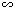$\Delta $OCE)

và \[\frac{\text{DO}}{\text{DB}}\text{ = }\frac{\text{OE}}{\text{OB}}\] (Do OC = OB) và \[\widehat{\text{DOE}}=\widehat{\text{B}}=\widehat{\text{C}}\]  nên $\Delta $DOE  $\Delta $DBO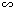$\Delta $OCE

c) Từ câu b suy ra \[{{\widehat{\text{D}}}_{\text{1}}}\text{ = }{{\widehat{\text{D}}}_{2}}\]$\Rightarrow $ DO là phân giác của các góc BDE

Củng từ câu b suy ra \[{{\widehat{\text{E}}}_{\text{1}}}\text{ = }{{\widehat{\text{E}}}_{2}}\] EO là phân giác của các góc CED

c) Gọi OH, OI là khoảng cách từ O đến DE, CE thì OH = OI, mà O cố định nên OH không đổi $\Rightarrow $OI không đổi khi D di động trên AB

Giải:

Gọi khoảng cách từ a, I, G đến BC lần lượt là AH, IK, GD

Vì I là giao điểm của ba đường phân giác nên khoảng cách từ I đến ba cạnh AB, BC, CA bằng nhau và bằng IK. Vì I nằm trong tam giác ABC nên:

S_ABC  = S_AIB + S_BIC + S_CIA $\Leftrightarrow $BC.AH = IK(AB+BC+CA) (1)

Mà  BC = $\frac{\text{AB + CA }}{\text{2}}$ $\Rightarrow $ AB + CA = 2 BC (2)

Thay (2) vào (1) ta có: BC. AH = IK. 3BC $\Rightarrow $ IK = $\frac{1}{3}$AH (a)

Vì G là trọng tâm của tam giác ABC nên:

S_BGC  = $\frac{1}{3}$ S_ABC $\Leftrightarrow $ BC . GD = $\frac{1}{3}$ BC. AH $\Rightarrow $ GD = $\frac{1}{3}$ AH (b)

Từ (a) và (b) suy ra IK = GD hay k/ cách từ  I, G đến BC bằng nhau nên IG // BC

C. Bài tập rèn luyện

Bài 1. Cho tam giác ABC vuông ở A, điểm M thuộc cạnh AC. Vẽ MD vuông góc BC tại D. Gọi E là giao điểm AB và MD.

a)  Chứng minh rằng:  ∆ABC≅∆DBE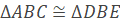     

b)  Chứng minh rằng: MA.MC = MD.ME

c)  Chứng minh rằng: ∆MAD≅∆MEC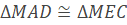   

d)  Chứng minh rằng: AB.AE = AM.AC

 Bài 2.  Cho tam giác ABC nhọn, các đường cao BD và CE

cắt nhau tại H. Chứng minh rằng:

a) ∆BAD∽∆CAE     

b)  HB.HD = HC.HE

c)  ∆BHC~∆DHE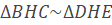    

d)  DH.DB = DA.DC

 Bài 3.  Cho tam giác nhọn ABC, các đường cao BD và CE cắt nhau ở H. Chứng minh rằng:

a)  Tam giác EHB đồng dạng tam giác DHC

b)  Tam giác HED đồng dạng tam giác HBC

c)  Tam giác ADE đồng dạng tam giác ABC

Bài 4.  Cho tam giác ABC có ba góc nhọn (AB < AC). Vẽ hai đường cao BD và CE.

a)  Chứng minh:  ΔABD đồng dạng ΔACE. Suy ra : AB.AE = CA.AD

b)  Chứng minh:  ΔADE đồng dạng ΔABC

c)  Tia DE và CB cắt nhau tại I. Chứng minh:  ΔIBE đồng dạng ΔIDC 

Bài 5. Cho hình thoi ABCD có góc A bằng 60⁰.

Qua C kẻ đường thẳng d không cắt hình thoi nhưng

cắt đường thẳng AB tại E và đường thẳng AD tại F.

a) Chứng minh: ∆BEC~∆AEF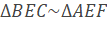

b) Chứng minh: ∆DCF~∆AEF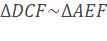 

c) Chứng minh:  BE.DF = DB².

d) Chứng minh: ∆BDE~∆DBF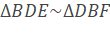 

Bài 6. Cho tam giác ABC có góc A = 90⁰, AB = 30cm, AC = 40cm, đường cao AE và BD là phân giác. Gọi F là giao điểm của AE và BD.

a) Chứng minh : Tam giác ABC đồng dạng tam giác EAC. Tính AE

b) Chứng minh : BD.EF = BF.AD

c) Chứng minh : AF = AD.

d) Tính AF.

Bài 7. Cho tam giác ABC có ba góc nhọn,đường cao BE và CF cắt nhau tại H

          a)  Chứng minh rằng :AE.AC = AF.AB

          b)  Tam giác AEF đồng dạng với tam giác ABC.

          c)  AH cắt BC tại D,ED cắt FC tại I.Chứng minh rằng: HI.CF = HF.IC.

Bài viết gợi ý: