Thể tích hình hộp chữ nhật

Thể tích hình hộp chữ nhật

I.Lý thuyết:

1. Đường thẳng vuông góc với mặt phẳng

Hai mặt phẳng vuông góc

a) Đường thẳng vuông góc với mặt phẳng

Nếu một đường thẳng vuông góc với một mặt phẳng tại điểm A thì nó vuông góc với mọi đường thẳng của mặt phẳng đi qua A.

b) Hai mặt phẳng vuông góc

Khi một tròn hai mặt phẳng (ABCD) và (A'B'C'D') chứa một đường thẳng vuông góc với mặt phẳng còn lại thì người ta nói hai mặt phẳng đó vuông góc với nhau.

Kí hiệu : mp (ABCD)⊥ mp ( (A'B'C'D')

2. Thể tích hình hộp chữ nhật 

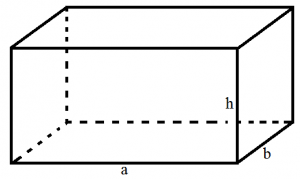
V = a.b.h

a, b, c là ba kích thước của hình hộp

Thể tích hình lập phương cạnh a là 

V = a³

II. Bài tập vận dụng:

Ví dụ 1: Một bể nước hình hộp chữ nhật có chiều dài 2m. Lúc đầu bể không có nước. Sau khi đổ vào bể 120 thùng nước, mỗi thùng chứa 20 lít thì mực nước của bể là 0,8m.

a) Tính chiều rộng của bể nước.

b) Người ta đổ thêm vào bể 60 thùng nước  nữa thì đầy bể. Hỏi bể cao bao nhiêu mét?

Hướng dẫn:

                                                                                     

 

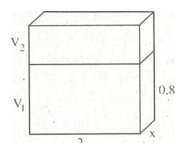
a) Thể tích nước đổ vào bể cũng chính là thể tích hình hộp chữ nhật có chiều dài 2m, chiều cao 0,8m.

b) Tỉ số của của mực nước tăng thêm so với mực nước đổ vào đợt 1 cũng bằng tỉ sô” thể tích nước tăng thêm so với thể tích nước đổ vào đợt 1.

Thể tích nước đổ vào bể đợt 1:

Vi = 20.120 = 2400 (l) = 2400dm³ = 2,4m

Chiều rộng của bể nước: 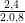  = 1,5 (m)

Tỉ số của mực nước tăng thêm so với mực nước đổ vào đợt 1:

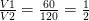
Mực nước tăng thêm là: 0,8. 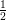 = 0,4 (m)

Độ cao của bể là: 0,8 + 0,4 = 1,2 (m).

Ví dụ 2: Một cái thùng hình lập phương, cạnh 7dm, có chứa nước với độ sâu của nước là 4dm. người ta thả 25 viên gạch có chiều dài 2dm, chiều rộng 1dm và chiều cao 0,5dm vào thùng. Hỏi nước trong thùng dâng lên cách miệng thùng bao nhiêu đề – xi  mét  ? (Giả thiết toàn bộ gạch ngập trong nước và chúng hút nước không đáng kể).

Hướng dẫn:

Áp dụng công thức tính thể tích hình hộp chữ nhật V = a.b.c và công thức tính thể tích hình lập phương V = a³.

Tính thể tích nước trong thùng lúc đầu V1.

Tính thể tích một viên gạch => thể tích của 25 viên gạch V2.

Mực nước dâng cao hơn trước: h =  

Mực nước cách miệng thùng: 7 – (h + 4).

                                                                                

 

Thể tích nước trong thùng lúc đầu:

V1 = 7.7.4 = 196 (dm³)

Thể tích một viên gạch:

2.1.0,5 = 1 (dm³)

Thể tích của 25 viên gạch:

1.25 = 25 (dm³)

Sau khi thả gạch vào, mực nước dâng cao hơn trước là: 

 

Khi đó mực nước cách miệng thùng:

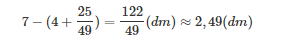
Ví dụ 3: Tính thể tích của khối gỗ có dạng:

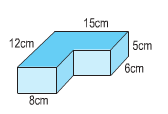
Thể tích hình hộp chữ nhật H là:

(15 - 8) x (12 - 6) x 5 = 210 (cm³)

Thể tích của cả khối gỗ và hình hộp chữ nhật B là:

15 x 12 x 5 = 900 (cm³)

Thể tích khối gỗ là:

900 - 210 = 690 (cm³)

Đáp số: 690cm³.

Ví dụ 4: Tính thể tích hình hộp chữ nhật có chiều dài a, chiều rộng b và chiều cao c:

a) a = 5cm; b = 4cm; c = 9cm

b) a = 1,5m; b = 1,1m; c = 0,5cm

c) a = 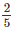dm; b = 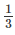dm; c = dm

Hướng dẫn :

a, Thể tích hình hộp chữ nhật là:

5 x 4 x 9 = 180 (cm³)

b, Thể tích hình hộp chữ nhật là:

1,5 x 1,1 x 0,5 = 0,825 (cm³)

Ví dụ 5: Tính thể tích của hòn đá nằm trong bể nước.

Hướng dẫn:

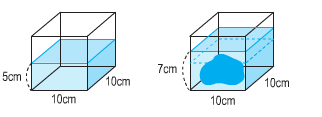
Cách 1: thể tích nước trong bể là:

10 x 10 x 5 = 500 (cm³)

Tổng thể tích của nước và hòn đá là:

10 x 10 x 7 = 700 (cm³)

Thể tích của hòn đá là:

700 – 500 = 200 (cm³)

Cách 2: chiều cao của mực nước dâng lên là:

7 – 5 = 2 (cm)

Thể tích nước dâng lên là:

10 x 10 x 2 = 200 (cm³)

Đó cũng chính là thể tích hòn đá

III. Bài tập tự luyện:

Bài 1: Thùng chứa của một xe chở hàng đông lạnh có dạng như hình 36. Một số mặt là những hình chữ nhật, chẳng hạn (ABKI), (DCC’D’)

– Quan sát hình và trả lời câu hỏi sau:

a) Những đường thẳng nào song song với mặt phẳng (ABKI)

b) Những đường thẳng nào vuông góc với mặt phẳng (DCC’D’)

c) Mặt phẳng (A’D’C’D’) có vuông góc với mặt phẳng (DCC’D’) hay không?

 

Bài 2: Cho hình hộp chữ nhật ABCD.EFGH

a) Kể tên các đường thẳng song song với mp (EFGH)

b) Đường thẳng AB song song với những mặt phẳng nào?

c) Đường thẳng AD song song với những đường thẳng nào?

 

Bài 3: Đố: Các kích thước của một hình hộp chữ nhật là 4cm, 3cm,  2cm. Một con kiến bò theo mặt của hình hộp đó từ Q đến P

a)Hỏi con kiến bò theo đường nào là ngắn nhất?

b) Độ dài ngắn nhất đó bằng bao nhiêu xentimet ?

 

Bài 4: Tính thể tích các hình sau biết mỗi cạnh 1cm:

 

 

Bài 5:

Một bể cá dạng hình hộp chữ nhật làm bằng kính ( không có nắp) có chiều dài 80 cm, chiều rộng 50 cm, chiều cao 45 cm.

Mực nước ban đầu trong bể cao 35 cm.

a) Tính diên tích kính dùng để làm bể cá đó.

b) Người ta cho vào bể một hòn đá có thể tích 10 dm3. Hỏi mực nước trong bể lúc này cao bao nhiêu xăng – ti-mét?

 Bài 6: Tính thể  tích hình sau:

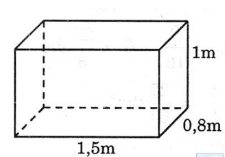
Bài 7: Tính thể tích hình sau:

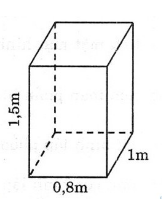
Bài 8: Tính thể tích của một hình hộp chữ nhật có diện tích xung quanh bằng 448 cm², chiều cao 8 cm, chiều dài hơn chiều rộng 4 cm

Bài 9: Tính thể tích hình hộp chữ nhật không nắp biết chiều dài 75 cm, chiều rộng 40 cm và chiều cao 35 cm.

Bài 10: Tính thể tích hình hộp chữ nhật có chiều dài a, chiều rộng b và chiều cao c:

a) a = 7 cm; b = 5 cm; c = 12cm

b) a = 3 m; b = 2 m; c = 1 m

 

Chúc các bạn học tốt.

Bài viết gợi ý: