Toán 6: Các dạng toán về thứ tự trong tập hợp các số nguyên âm
Dạng 1: SO SÁNH CÁC SỐ NGUYÊN
Phương pháp giải
Cách 1 :
– Biểu diễn các số nguyên cần so sánh trên trục số
– Giá trị các số nguyên tăng dần từ trái sang phải.
Cách 2 : Căn cứ vào các nhận xét sau :
– Số nguyên dương lớn hơn 0
– Số nguyên âm nhỏ hơn 0
– Số nguyên dương lớn hơn số nguyên âm
– Trong hai số nguyên dương, số nào có giá trị tuyệt đối lớn hơn thì số ấy lớn hơn
– Trong hai số nguyên âm, số nào có giá trị tuyệt đối nhỏ hơn thì số ấy lớn hơn.
Ví dụ 1:
Điền dấu ( > < = ) thích hợp vào chỗ trống:
3…5 -3…-5 4…-6 10…-10.
Trả lời
3< 5 -3 > -5 4 > -6 10 > -10.
Ví dụ 2:
Sắp xếp các số nguyên sau theo thứ tự tăng dần :
2, -17 , 5 , 1 , -2 , 0.
Sắp xếp các số nguyên sau theo thứ tự giảm dần :
-101, 15 , 0, 7, -8, 2001.
Trả lời
a) -17 < -2 < 0 < 1 < 2 < 5.
b) 2001 >15 >7 >0 > -8 > -101.
Ví dụ 3:
a) Số nguyên a lớn hơn 2. Số a có chắc chắn là số nguyên dương không ?
b) Số nguyên b nhỏ hơn 3. Số b có chắc chắn là số nguyên âm không ?
c) Số nguyên c lớn hơn -1. Số c có chắc chắn là số nguyên dương không ?
d) Số nguyên d nhỏ hơn -5. Số d có chắc chắn là số nguyên âm không ?
Giải
a) Trên trục số, điểm a nằm bên phải điểm 2 nên nó cũng nằm bên phải điểm 0. Vậy số a
chắc chắn là số nguyên dương.
b) b < 3 thì b có thể là 0, 1, 2. Vậy số b không chắc chắn là số nguyên âm.
c) c > -1 thì c có thể là 0. Vậy số c không chắc chắn là số nguyên dương.
d) Trên trục số, điểm d nằm bên trái điểm – 5 nên nó cũng nằm bên trái điểm 0. Vậy d
chắc chắn là số nguyên âm.
Ví dụ 4 : Điền dấu “+” hoặc vào chỗ trống để được kết quả đúng:
a) 0 < … 2 ; b)… 15 < 0 ;
c)… 10 < … 6 ; d)… 3 < … 9.
(Chú ý : có thể có nhiều đáp số).
Giải
a) 0 < +2 ; b) -15 < 0 ;
c) -10 < -6 ; -10 < +6 ; d) +3 < +9 ; -3 < +9.
Dạng 2. TÌM CÁC SỐ NGUYÊN THUỘC MỘT KHOẢNG CHO TRƯỚC
Phương pháp giải
– Vẽ trục số và thể hiện khoảng cho trước trên trục số;
– Tìm trên trục số các số nguyên thuộc khoảng đã cho.
Ví dụ :
Tìm x ∈ Z , biết:
a) -5 < x < 0 b) -3 < x < 3.
Giải
a)Vẽ trục số và biểu diễn các điểm -5 và 0 trên trục số :
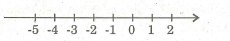
Các điểm nguyên x thỏa mãn – 5 < x < 0 sẽ nằm bên phải điểm -5 và bên trái điểm 0.
Vậy x <= {-4 ;-3 ;-2 ; 1}.
b) Giải tương tự câu a): x ∈ {-2 ;-l ;0 ; 1; 21.
Dạng 3. CỦNG CỐ KHÁI NIỆM GIÁ TRỊ TUYỆT ĐỐI CỦA MỘT SỐ NGUYÊN
Phương pháp giải
Việc giải dạng toán này cần dựa trên các kiến thức sau về giá trị tuyệt đối của một số
nguyên :
– Giá trị tuyệt đối của một số tự nhiên là chính nó ;
– Giá trị tuyệt đối của một số nguyên âm là số đối của nó
– Giá trị tuyệt đối của một số nguyên là một số tự nhiên
– Hai số nguyên đối nhau có cùng một giá trị tuyệt đối.
Ví dụ 1:
Tìm giá trị tuyệt đối của các số : 2000 ; – 3011 ; -10.
Giải
|2000| = 2000 ; |-301l| = 3011 ; |-10| = 10 .
Ví dụ 2:
Điền dấu ( > < = ) thích hợp vào chỗ trống:
|3| … |5|, |-3| … |-5|, |-1| … |0|, |2| … |-2|.
Giải
|3|=3, |5| = 5 => |3| < |5|
|-l|=l, |0| = 0 => |-1| > |o|
|-3|=3, |-5| = 5 => |-3| < |-5|
|2|=2, |-2| = 2 =>|2| = |-2|.
Ví dụ 3:
Tính giá trị các biểu thức :
a)|-8|-|-4| ; b) |-7|.|-3|.
c)|18|: |-6| ; d) |-153| + |-53|.
Giải
a) |-8|-|-4| = 8-4 = 4;
b) |-7|.|-3| = 7.3 = 21
c) |18|: |-6| = 18 :6 = 3
d) |153| + |-53| = 153 + 53 = 206.
Ví dụ 4:
Tìm số đối của các số : -4 ; 6 ; |-5| ; |3|; 4.
Giải
Số đối của -4 là 4, của 6 là – 6, của |-5| = 5 là -5, của |3| = 3 là -3, của 4 là – 4.
Dạng 4. CỦNG CỐ LẠI VỀ TẬP HỢP N CÁC SỐ TỰ NHIÊN VÀ TẬP HỢP Z CÁC
SỐ NGUYÊN
Phương pháp giải
Cần nắm vững : N = {0 ; 1; 2 ; 3 ; 4 ;…};
Z ={… -3 ; -2 ; -1 ; 0 ; 1; 2 ; 3 ; …}.
Ví dụ 1:
Điền chữ Đ (đúng) hoặc chữ S (sai) vào ô vuông :
7 ∈ N … ; 7 ∈ Z …; 0 ∈ N … ; 0 ∈ Z…;
-9 ∈ Z … ; -9 ∈ N … ; 11,2 ∈ Z ….
Giải
7 ∈ N (Đ) ; 7 ∈ Z (Đ); 0 ∈ N (Đ) ; 0 ∈ Z (Đ);
-9 ∈ Z (Đ) ; -9 ∈ N (S) ; 11,2 ∈ Z (S)
Ví dụ 2:
Có thể khẳng định rằng tập hợp Z bao gồm hai bộ phận là các số nguyên dương và các số
nguyên âm được không ? Tại sao ?
Trả lời
Không khẳng định được vì còn thiếu số 0.
Dạng 5. BÀI TẬP VỀ SỐ LIỀN TRƯỚC, SỐ LIỀN SAU CỦA MỘT SỐ NGUYÊN
Phương pháp giải
Cần nắm vững : số nguyên b gọi là số liền sau của số nguyên a nếu a < b và không có
số nguyên nào nằm giữa a, b ; khi đó, ta cũng nói a là số liền trước của b.
Ví dụ :
a) Tìm số liền sau của mỗi số nguyên sau : 2 ; -8 ; 0 ; -1.
b) Tìm số liền trước của mỗi số nguyên sau : -4 ; 0 ; 1 ; -25.
c) Tìm số nguyên a biết số liền sau a là một số nguyên dương và số liền trước a là một
số nguyên âm.
Trả lời
a) 3 ; -7 ; 1 ; 0 b)-5 ;-1 ; 0 ;-26 c) a = 0.
CHÚC CÁC BẠN HỌC TỐT NHÉ <3







