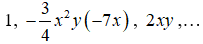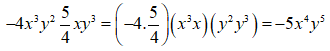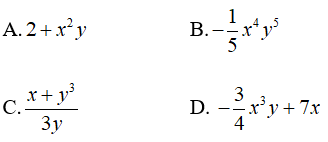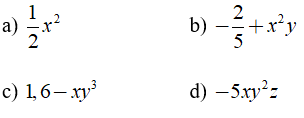A. Lý thuyết
1. Đơn thức
Đơn thức là biểu thức đại số chỉ gồm một số, hoặc một biến, hoặc một tích giữa các số và các biến.
Ví dụ:
Chú ý: Số 0 được gọi là đơn thức không
2. Đơn thức thu gọn
Đơn thức thu gọn là đơn thức chỉ gồm tích của một số với các biến mà mỗi biến đã được nâng lên lũy thừa với số mũ nguyên dương. Số nói trên gọi là hệ số, phần còn lại gọi là biến của đơn thức thu gọn.
Ví dụ: Các đơn thức x, -y, 3x2y, 10xy5 là những đơn thức thu gọn, có hệ số lần lượt là 1, -1, 3, 10 và có phần biến lần lượt là x, y, x2y, xy5.
Chú ý:
+ Ta cũng coi một số là đơn thức thu gọn.
+ Trong đơn thức thu gọn, mỗi biến chỉ được viết một lần. Thông thường, khi viết các đơn thức thu gọn ta viết hệ số trước, phần biến sau và các biến được viết theo thứ tự bảng chữ cái.
3. Bậc của một đơn thức
• Bậc của đơn thức có hệ số khác 0 là tổng số mũ của tất cả các biến có trong đơn thức đó.
• Số thực khác 0 là đơn thức bậc không.
• Số 0 được coi là đơn thức không có bậc.
4. Nhân hai đơn thức
Để nhân hai đơn thức, ta nhân các hệ số với nhau và nhân các phần biến với nhau
Ví dụ:
Ta có
+ Hệ số: -5.
+ Phần biến: x4y5
+ Bậc của đơn thức: 9.
Chú ý: Mỗi đơn thức đều có thể viết thành một đơn thức thu gọn.
B. Trắc nghiệm & Tự luận
Bài 1: Trong các biểu thức đại số sau, biểu thức nào không phải đơn thức?
A. 2 B. 5x + 9 C. x3y2 D. 3x
Lời giải :
Biểu thức 5x + 9 không phải đơn thức
Chọn đáp án B
Bài 2: Trong các biểu thức đại số sau, biểu thức nào là đơn thức?
Lời giải :
Biểu thức (-1/5)x4y5 là đơn thức
Chọn đáp án B
Bài 3: : Sau khi thu gọn đơn thức 2.(-3.x3.y)y2 ta được đơn thức
A. -6x3y3 B. 6x3y3 C. 6x3y2 D. -6x2y3
Lời giải :
Ta có 2.(-3x3y).y2 = 2.(-3)x3.y.y2 = -6x3y3
Chọn đáp án A
Bài 4: Trong các biểu thức dưới đây, chỉ ra đâu là đơn thức? Nếu là đơn thức, hãy chỉ ra đâu là hệ số, đâu là phần biến của mỗi đơn thức đó.
Lời giải :
Các biểu thức a) và d) là đơn thức vì chúng gồm tích của số và biến
a) Phần số là 1/2 , phần biến là x2
d) Phần số là -5 , phần biến là xy2z
Các biểu thức còn lại là b) và c) không phải là đơn thức.
Bài 5: Hãy viết các đơn thức bậc ba với biến x, y và có giá trị bằng 2 tại x = 1, y = -1
Lời giải :
Đơn thức với biến x, y có dạng: k.xt.ys với t + s = 3, t,s ≥ 1 (vì đa thức này bậc ba)
Từ đây ta suy ra t, s < 3
Tại x = 1, y = -1 thì 2 = k.xt.ys = k.(1)t.(-1)s = k.(-1)s
+ Với s = 1, khi đó k.(-1)1 = 2 ⇒ k = -2, t = 3 - 1 = 2
Đơn thức cần tìm là -2x2y
+ Với s = 2, khi đó k.(-1)2 = 2 ⇒ k = 2, t = 3 - 2 = 1
Đơn thức cần tìm là 2xy2
Vậy các đơn thức thỏa mãn yêu cầu bài là: -2x2y; 2xy2
C.Bài tập tự luyện
Bài 1: Tính giá trị của đơn thức 5.x4.y2.z3 tại x = -1, y = -1, z = -2
A. 10 B. 20 C. -40 D. 40
Bài 2: Tìm hệ số trong đơn thức -36a2.b2.x2.y3 với a, b là hằng số
A. -36 B. -36a2b2 C. 36a2b2 D. -36a2
Bài 3: Tìm phần biến trong đơn thức 100abx2yz với a, b là hằng số.
A. ab2x2yz B. x2y C. x2yz D. 100ab
Bài 4: Trong các biểu thức sau, biểu thức nào là đơn thức:
a. 3/4
b. 1/2x2yz
c. 3 + x2
d. 3x2
Bài 5: Cho 5 ví dụ đơn thức bậc 4 có các biến là x, y, z
Bài 6: Cho các chữ x, y. Lập hai biểu thức đại số mà:
- Một biểu thức là đơn thức
- Một biểu thức không phải là đơn thức
Bài 7: Thu gọn các đơn thức và chỉ ra phần hệ số của chúng:
a. 5x2.3xy2
b. 1/4 (x2y3)2.(-2xy)
Bài 8: Viết các đơn thức sau dưới dạng thu gọn:
a. 2/3 xy2z.(-3x2y)2
b. x2yz.(2xy)2z
Bài 9: Bậc của đơn thức 3y2 (2y2)3y sau khi đã thu gọn là:
(A) 6;
(B) 7;
(C) 8;
(D) 9.
Bài 10: Tính tích các đơn thức sau và tìm bậc của đơn thức thu được:
a) 4xy2 và (-3)/4 (x2 y)3
b) 1/6x(2y3)2 và -9x5y
D.Gợi ý đáp án
Bài 1:
Thay x = -1, y = -1, z = -2 vào đơn thức 5.x4.y2.z3 ta được 5.(-1)4.(-1)2.(-2)3 = -40
Chọn đáp án C
Bài 2:
Đơn thức -36a2.b2.x2.y3 với a, b là hằng số có hệ số là -36a2.b2
Chọn đáp án B
Bài 3:
Đơn thức 100abx2yz với a, b là hằng số có phần biến số là x2yz
Chọn đáp án C
Bài 4:
a. 3/4 là đơn thức
b. 1/2x2yz là đơn thức
c. 3 + x2 không phải là đơn thức (đa thức)
d. 3x2 là đơn thức
Bài 5:
5 ví dụ đơn thức bậc 4 có các biến là x, y, z là:
4x2yz; -5xy2z;
3xyz2; 6xyz2; -2x2yz
Bài 6:
- Biểu thức là đơn thức: 3xy
- Biểu thức không phải là đơn thức: 2x + y
Bài 7:
a. Ta có: 5x2.3xy2 = (5.3).(x2.x).y2 = 15x3y2
Phần hệ số: 15
b. 1/4 (x2y3)2.(-2xy) = 1/4 .(-2)x4y6.xy = - 1/2 (x4.x)(y6.y) = - 1/2 x5y7
Phần hệ số: - 1/2
Bài 8:
a. Ta có: -2/3 xy2z.(-3x2y)2 = -2/3 xy2z.9x4y2
= (-2/3 .9)(x.x4).(y2.y2).z = -6x5y4z
b. Ta có: x2yz.(2xy)2z = x2yz.4x2y2.z = 4(x2.x2)(y.y2)(z.z) = 4x4y3z2
Bài 9:
Chọn đáp án D
Bài 10:
a) 4xy2. [(-3)/4.(x2 y)3]
= 4xy2.[(-3)/4.x6.y3]
= [4.(-3)/4].(x.x6).(y2.y3)
= -3.x7.y5.
Đơn thức có bậc bằng 7 + 5 = 12.
b) 1/6x(2y3)2.(-9.x5y)
= 1/6.x.4y6.(-9).x5.y
= [1/6.4.(-9)].(x.x5).(y6.y)
= -6.x6.y7
Đơn thức có bậc 6 + 7 = 13.