Bài toán thực tế liên quan đến hình học
Bài toán thực tế liên quan đến hình học thường xoay quanh một số nội dung như sau: Tính toán để đường đi được ngắn nhất, tính toán để diện tích được lớn nhất, hay cũng có thể đơn giản là tính diện tích hoặc thể tích của một vật…
Bài 1. Một sợi dây có chiều dài 6m được chia thành hai phần. Một phần được uốn thành hình tam giác đều và một phần được uốn thành hình vuông. Hỏi độ dài cạnh của hình tam giác đều bằng bao nhiêu để tổng diện tích hai hình thu được là nhỏ nhất.
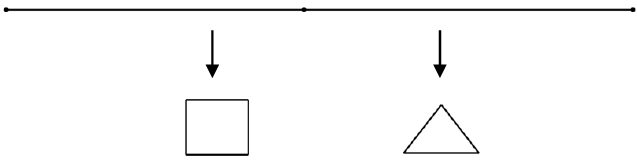
A.$\frac{54-24\sqrt{3}}{11}m$ B. \[\frac{36\sqrt{3}}{13}m\] C. $\frac{48-12\sqrt{3}}{13}m$ D. $\frac{-54+72\sqrt{3}}{13}m$
Giải:
Gọi độ dài cạnh hình tam giác đều là x ( x > 0), ta có cạnh hình vuông là :$\frac{6-3x}{4}.$
Tổng diện tích của hai hình là:$S=\frac{{{x}^{2}}\sqrt{3}}{4}+{{\left( \frac{6-3x}{4} \right)}^{2}}=\frac{1}{16}\left[ (9+4\sqrt{3}){{x}^{2}}-36x+36 \right].$
${{S}_{\min }}$ khi $x=-\frac{-36}{2(9+4\sqrt{3})}\Leftrightarrow x=\frac{54-24\sqrt{3}}{11}$
Bài 2. Bác nông dân làm một hàng rào trồng rau hình chữ nhật có chiều dài song song với bờ tường. Bác chỉ làm ba mặt vì mặt thứ tư bác tận dụng luôn bờ tường. Bác dự tính sẽ dùng 200m lưới sắt để làm nên toàn bộ hàng rào đó. Hỏi diện tích lớn nhất bác có thể rào là bao nhiêu.
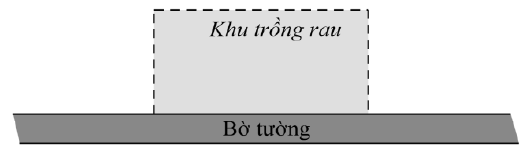
A.$1500{{m}^{2}}$ B. $10000{{m}^{2}}$ C. $2500{{m}^{2}}$ D. $5000{{m}^{2}}$
Giải:
Gọi chiều dài và chiều rộng của khu đất rào được là x và y (0 < y < x < 200).
Ta có:$x+2y=200\Leftrightarrow x=200-2y.$
Diện tích rào được :$f(y)=x.y=(200-2y).y=-2{{y}^{2}}+200y.$
Diện tích lớn nhất khi :$y=-\frac{200}{2(-2)}=50\Rightarrow x=100\Rightarrow m\text{axS=5000}\text{.}$
Bài 3: Bạn Hoa đi từ nhà ở vị trí A đến trường tại vị trí C phải đi qua cầu từ A đến B rồi từ B đến trường. Trận lũ vừa qua cây cầu bị ngập nước, do đó bạn Hoa phải đi bằng thuyền từ nhà đến vị trí D nào đó trên đoạn BC với vận tốc 4 km/h sau đó đi bộ với vận tốc 5 km/h đến C. Biết độ dài AB = 3km, BC = 5 km. Hỏi muộn nhất mấy giờ bạn Hoa phải xuất phát từ nhà để có mặt ở AB trường lúc 7 h 30 phút sáng kịp vào học.

A. 6 h 03 phút; B. 6 h 16 phút; C. 5 h 30 phút; D. 5 h 45 phút.
Giải:
Ta sẽ tính xem bạn Hoa cần ít nhất bao nhiêu thời gian để đi từ A đến C.
Giả sử$CD=x,(0
Thời gian Hoa di từ A đến C là :$f(x)=\frac{\sqrt{{{x}^{2}}-10x+34}}{4}+\frac{x}{5}\Rightarrow f'(x)=\frac{x-5}{4\sqrt{{{x}^{2}}-10x+34}}+\frac{1}{5}.$
Ta có:$f'(x)=0\Leftrightarrow x=1$ .Mà $f(1)=1,45$.Như vậy bạn Hoa cần ít nhất 1 h 27 phút để di chuyển do đó muộn nhất 6h03phút Hoa phải xuất phát.
Bài 4. Người ta lắp đặt đường dây điện nối từ điểm A trên bờ AC đến điểm B trên một hòn đảo; khoẳng cách ngắn nhất từ B đến AC bằng 3 km, khoảng cách từ A đến C là 12 km. Chi phí lắp đặt mỗi km dây điện dưới nước là 100 triệu đồng, còn trên bờ là 80 triệu đồng. Hỏi phải chọn điểm S trên bờ AC cách A bao nhiêu để chi phí mắc dây điện từ A đến S rồi từ S đến B là thấp nhất.
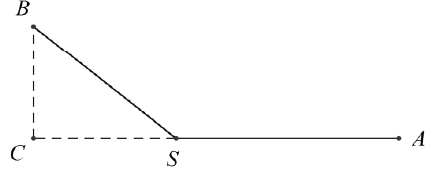
A. 4 km; B. 8 km; C. 6 km; D. 10 km.
Giải:
Giả sử\[AS=x,(0
Số tiền để mắc đường dây điện là:$f(x)=80x+100\sqrt{{{x}^{2}}-24x+153}$
Ta có:$f(4)=1174,400375,f(8)=1140,f(6)=1150,820393,f(10)=1160,555123.$
Suy ra: x = 8.
Bài 5. Hai vị trí A và B cách nhau 615 m và cùng nằm về một phía bờ sông. Khoảng cách từ A và từ B đến bờ sông lần lượt là 118 m và 487 m. Một người đi từ A đến bờ sông để lấy nước mang về B. Đoạn đường ngắn nhất mà người đó có thể đi là bao nhiêu (làm tròn đến chữ số thập phân thứ nhất).
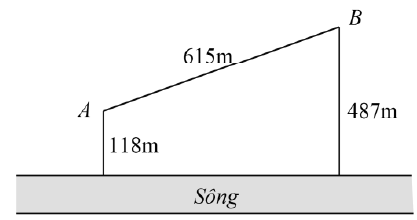
A. 569,5 m; B. 671,4 m; C. 779,8 m; D. 741,2 m.
Giải:
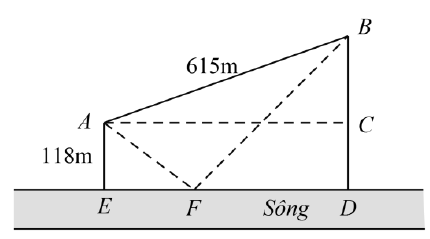
Ta có :$ED=AC=492$
Đặt \[\text{EF=x}\Rightarrow \text{FD=492-x}\]
Đoạn đường mà người đó phải đi là:
$f(x)=\sqrt{{{x}^{2}}+{{118}^{2}}}+\sqrt{{{(492-x)}^{2}}+{{487}^{2}}}$
$\Leftrightarrow f(x)=\sqrt{{{x}^{2}}+13924}+\sqrt{{{x}^{2}}-984x+479233.}$
Ta có:
$f'(x)=\frac{x}{\sqrt{{{x}^{2}}+13924}}+\frac{x-492x}{\sqrt{{{x}^{2}}-984x+479233}}$
Do đó:$f'(x)=0\Leftrightarrow x=\frac{58056}{605}$ . Suy ra đoạn đường ngắn nhất có thể đi là:$f(\frac{59056}{605})=779,8$
Bài 6. Có hai chiếc cọc cao 10 m và 30 m lần lượt đặt tại hai vị trí A, B. Biết khoảng cách giữa hai cọc bằng 24 m. Người ta chọn một cái chốt ở vị trí M trên mặt đất nằm giữa hai chân cột để giăng giây nối đến hai đỉnh C và D của cọc như hình vẽ. Hỏi ta phải đặt chốt ở vị trí nào để tổng độ dài của hai sợi dây đó là ngắn nhất.
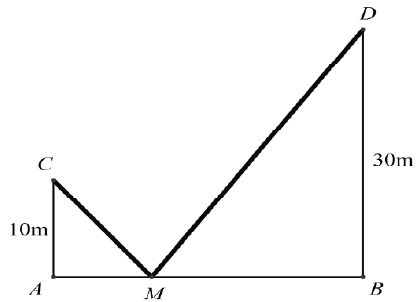
A. AM = 6 m, BM = 18 m B. AM = 7 m, BM = 17 m
C. AM = 4 m, BM = 20 m D. AM = 12 m, BM = 12 m
Giải:
Đặt$AM=x,(0
$f(x)=\sqrt{{{10}^{2}}+{{x}^{2}}}+\sqrt{{{30}^{2}}+{{(24-x)}^{2}}}$
Ta có:
$f(6)=8\sqrt{34};f(7)=46,68843491;f(4)=2\sqrt{29}+10\sqrt{13};f(12)=2\sqrt{61}+6\sqrt{29}.$
Bài 7. Từ một mảnh giấy hình vuông cạnh 4 cm, người ta gấp nó thành 4 phần đều nhau rồi dựng lên thành một hình lăng trụ tứ giác đều như hình vẽ. Hỏi thể tích của lăng trụ này là bao nhiêu.
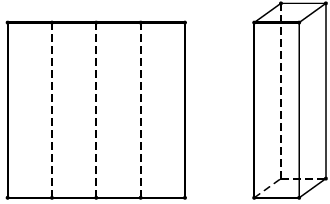
A.$4c{{m}^{3}}$ B. $16c{{m}^{3}}$ C. $\frac{4}{3}c{{m}^{3}}$ D. $\frac{16}{3}c{{m}^{3}}$
Giải:
$V=1.1.4=4(c{{m}^{3}})$ Đáp án: A
Bài 8. Một người lính đặc công thực hiện bơi luyện tập từ vị trí A trên bờ biển đến một cái thuyền đang neo đậu ở vị trí C trên biển. Sau khi bơi được 1,25 km do khát nước người này đã bơi vào vị trí E trên bờ để uống nước rồi mới từ E bơi đến C. Hãy tính xem người lính này phải bơi ít nhất bao nhiêu km. Biết rằng khoảng cách từ A đến C là 6,25 km và khoảng cách ngắn nhất từ C vào bờ là 5 km.
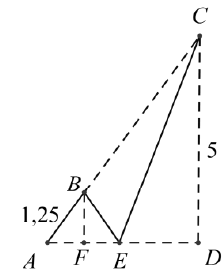
A.$3\sqrt{5}km.$ B.$\sqrt{29}+\sqrt{2}km.$ C.$\sqrt{26}+\sqrt{5}km.$ D.$\frac{5+12\sqrt{5}}{4}km.$
Giải:
Giả sử . EF = x
Suy ra quãng đường mà người này phải bơi là:$S(x)=1,25+\sqrt{{{1}^{2}}+{{x}^{2}}}+\sqrt{{{5}^{2}}+{{(3-x)}^{2}}}$
Đáp án: D
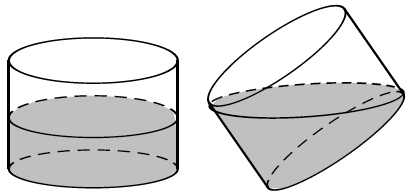
Bài 9. Đổ nước vào một chiếc thùng hình trụ có bán kính đáy 20 cm. Nghiêng thùng sao cho mặt nước chạm vào miệng cốc và đáy cốc như hình vẽ thì mặt nước tạo với đáy cốc một góc 45o. Hỏi thể tích của thùng là bao nhiêu cm3.
A.$16000\pi $ B. $12000\pi $ C. $8000\pi $ D. $6000\pi $
Giải:
Do mặt nước tạo với mặt đáy góc 450 nên chiều cao của hình trụ bằng đường kính của đáy.
Đáp án: A
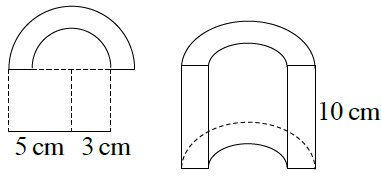
Bài 10. Tính thể tích của một chi tiết máy trong hình biết rằng mặt cắt được cắt theo phương vuông góc với trục thẳng đứng.
A.$50\pi c{{m}^{3}}$ B. $60\pi c{{m}^{3}}$ C. $80\pi c{{m}^{3}}$ D. $90\pi c{{m}^{3}}$
Giải:
$V=\frac{10\pi ({{5}^{2}}-{{3}^{2}})}{2}=80\pi .$







