Câu 1: Một chất điểm dao động điều hòa có phương trình x= A cos (ωt + ϕ) , tại thời điểm ban đầu vật đi qua vị trí có li độ x =0,5A và đang chuyển động về gốc tọa độ thì pha ban đầu ϕ bằng
A.\[\frac{\pi }{2}\] B.\[\frac{\pi }{6}\] C.\[\frac{\pi }{3}\] D.\[\frac{-\pi }{2}\]
Hướng dẫn
Tại thời điểm ban đầu:
$\left\{ \begin{aligned}& x=\frac{A}{2}\\& v<0 \\\end{aligned} \right.\Rightarrow \varphi =\frac{\pi }{3}$
Chọn đáp án C
Câu 2: Một vật dao động điều hòa với biên độ A, tần số góc ω . Chọn gốc thời gian là lúc vật đi qua vị trí mà vận tốc bằng 0 và sau đó nó đi theo chiều âm. Phương trình dao động của vật là
A.x=Asin(\[\omega t\])
B. x=Asin(\[\omega t\]\[-\frac{\pi }{2}\])
C. x=Asin(\[\omega t\]\[+\frac{\pi }{2}\])
D.x=Asin(\[\omega t\]+\[\pi \])
Hướng dẫn
Giả sử phương trình dao động của vật có dạng x = A cos (w t + j)
Tại thời điểm ban đầu vận tốc vật bằng 0 suy ra x = ±A , sau đó vật đi theo chiều âm nên tại thời điểm ban đầu vật ở biên dương x=A
\[\Rightarrow \] x=Acos (\[\omega \]t) = Asin (\[\omega \]t+\[\frac{\pi }{2}\])
Chọn đáp án C
Câu 3: Một vật dao động điều hòa v ới biênđộ A, tần số góc w. Chọn gốc thời gian là lúc vật đi qua vị trí có tọa độ âm và có vận tốc bằng -wA / 2 . Phương trình dao động là
A. x=Asin (\[\omega \]t)
B. x=Asin (\[\omega \]t - \[\frac{2\pi }{3}\])
C. x=Asin (\[\omega \]t + \[\frac{2\pi }{3}\])
D. x=Asin (\[\omega \]t + \[\pi \])
Hướng dẫn
Giả sử phương trình dao động của vật có dạng x = A sin (wt + j)
Ta có:
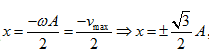
mặt khác vật đi qua vị trí có tọa độ âm nên \[x=-\frac{\sqrt{3}}{2}A\]
Tại thời điểm ban đầu:
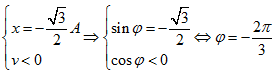
Chọn đáp án B
Câu 4: Một dao động điều hòa có chu kì dao động là 4s. Thời gian ngắn nhất để vật đi từ điểm có li độ cực đại về điểm có li độ bằng một nửa biên độ cực đại là
A.1/3s B.2/3s C.5s D.4s
Hướng dẫn
Thời gian ngắn nhất đểvật đi từ điểm có li độ cực đại về điểm có li độ bằng một nửa biên độ cực đại là: \[\vartriangle t={{t}_{\left( A\to \frac{A}{2} \right)}}=\frac{T}{6}=\frac{2}{3}(s)\]
Chọn đáp án B
Câu 5: Một chất điểm dao động điều hòa trên đoạn đường PQ, thời gian vật đi từ P đến Q là 0,25s. Gọi O, E lần lượt là trung điểm của PQ và OQ. Thời gian ngắn nhất vật đi từ E đến Q là
A. 1/ 24s B. 1 /16s C. 1 / 6s D. 1 /12s
Hướng dẫn
Ta có thời gian vật đi từ P đến Q là \[\frac{T}{2}=0,25s\Rightarrow T=0,5s\]
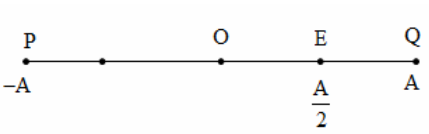
Thời gian ngắn nhất vật đi từ E đến Q là \[\vartriangle t={{t}_{\left( \frac{A}{2}\to A \right)}}=\frac{T}{6}=\frac{1}{12}(s)\]
Chọn đáp án D
Câu 6: Một chất điểm dao động điều hòa với chu kì T . Khoảng thời gian trong một chu kì để vật cách vị trí cân bằng một khoản nhỏ hơn \[0,5\sqrt{3}\]biên độ là:
A.T/3 B.2T/3 C.T/6 D.T/2
Hướng dẫn
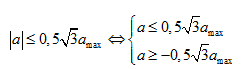
Lấy bên trong ứng với \[\alpha =\frac{4\pi }{3}\Leftrightarrow \vartriangle t=\frac{2T}{3}\]
Chọn đáp án B
Câu 7: Một chất điểm dao động điều hòa với chu kì T. Khoảng thời gian trong một chu kì đểvật cách vị trí cân bằng một khoảng lớn hơn \[0,5\sqrt{2}\] biên độ là
A.T/3 B.2T/3 C.T/6 D.T/2
Hướng dẫn
Ví trí vật cách cân bằng khoảng \[0,5\sqrt{2}A\]là \[x=\pm 0,5\sqrt{2}A\]
Từ 2 vị trí này ra biên, lấy rìa ngoài ứng với góc \[\alpha =4.\frac{\pi }{4}=\pi \Leftrightarrow \vartriangle t=\frac{T}{2}\]
Chọn đáp án D
Câu 8: Một chất điểm dao động điều hòa với chu kì T. Khoảng thời gian trong một chu kỳ đểvật có độ lớn gia tốc lớn hơn \[\frac{1}{2}\]gia tốc cực đại là
A.T/3. B.2T/3. C.T/6. D.T/12.
Hướng dẫn
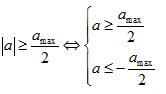
lấy 2 rìa ngoài ứng với \[\alpha =4\frac{\pi }{3}\Leftrightarrow \vartriangle t=\frac{2T}{3}\]
Chọn đáp án B
Câu 9: Một vật dao động điều hòa với chu kì T trên đoạn thẳng PQ. Gọi O, E lần lượt là trung điểm của PQ và OQ . Thời gian để vật đi từO đến Q rồi đến E là
A.5T/6. B.5T/12. C.T/12. D.7T/12.
Hướng dẫn
Tại P, Q là 2 biên. Đi từ O →Q hết T/4, từ Q →E hết T/6 \[\Rightarrow \] tổng thời gian = T/4 + T/6 = 5T/12
Chọn đáp án B
Câu 10: Một vật dao động điều hòa với phương x= 8cos 2πt (cm) , t đo bằng giây. Vật phải mất thời gian tối thiểu bao nhiêu giây để đi từ vị trí x = 8cm về vị trí
x= 4cm mà vectơ vận tốc cùng hướng với hướng của trục tọa độ
A. 1/3s. B.5/6s. C.1/2s. D.1/6s.
Hướng dẫn
Ta có: T = 1s.
Véc tơ v cùng chiều với hướng trục tọa độ (theo chiều dương)
\[\Rightarrow \] lấy x ở nửa dưới.
\[\Rightarrow \]Từ x = +8 cm →x = 4 cm hết thời gian = T/2 + T/4 + T/12 = 5T/6 = 5/6 s.
Chọn đáp án B
Câu 11: Một chất điểm đang dao động điều hòa trên một đoạn thẳng xung quanh vị trí cân bằng O. Gọi M, N là hai điểm trên đường thẳng cùng cách đều O. Biết cứ 0,05 s thì chất điểm lại đi qua các điểm M , N, O. Chu kì bằng
A. 0,3s. B. 0, 4s. C. 0, 2s. D. 0,1s.
Hướng dẫn
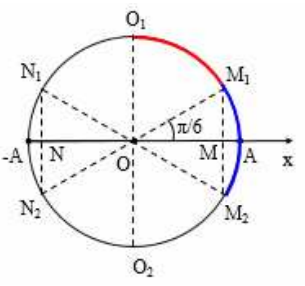
Theo đề bài thì M, N nằm đối xứng với nhau qua O như hình vẽ.
Mà sau mỗi khoảng thời gian 0,05 s thì chất điểm lại đi qua một trong
các vị trí M, N, O nên các điểm trên vòng tròn \[{{O}_{1}},{{N}_{1}},{{N}_{2}},{{O}_{2}},{{M}_{2}},{{M}_{1}}\] là cách đều nhau: \[\widehat{MO{{O}_{1}}}=\frac{2\pi }{6}=\frac{\pi }{3}\Rightarrow \frac{T}{6}=0,05\Rightarrow T=0,3s\]
Chọn đáp án A
Câu 12: Một chất điểm đang dao động điều hòa trên một đoạn thẳng. Trên đoạn thẳng đó có năm điểm theo đúng thứ tự M, N,O,P và Q với O là vị trí cân bằng. Biết cứ 0,05s thì chất điểm lại đi qua các điểm M, N,O,P và Q. Tốc độ của nó đi qua các điểm N,P là 20 πcm / s. Biên độ A bằng
A.4cm B.5cm C.\[4\sqrt{2}\]cm D.\[4,5\sqrt{2}\]cm
Hướng dẫn
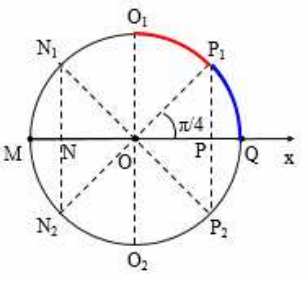
M, N, O, P, Q chia đường tròn thành 8 phần bằng nhau
\[\Rightarrow T=8.0,05=0,4s\Rightarrow \omega =5\pi rad/s\]
\[{{v}_{N}}=\frac{{{v}_{\max }}}{\sqrt{2}}\Leftrightarrow 20\pi =\frac{A.5\pi }{\sqrt{2}}\Rightarrow A=4\sqrt{2}cm\]
Chọn đáp án C
Câu 13: Một vật dao động điều hòa dọc theo trục Ox , quanh vị trí cân bằng O với biên độ A và chu kì T . Trong khoảng thời gian T/ 4 , quãng đường lớn nhất mà vật có thể đi được là
A.2A B.4A C.\[A\sqrt{3}\] D.\[A\sqrt{2}\]
Hướng dẫn
\[\vartriangle t=\frac{T}{4}\Leftrightarrow \varphi =\frac{\pi }{2}\] khi đó \[{{S}_{\max }}=2A\sin \frac{\vartriangle \varphi }{2}=2A\sin \frac{\pi }{4}=A\sqrt{2}\]
Chọn đáp án D
Câu 14: Một vật dao động điều hòa với biên độ A và chu kì T . Thời gian ngắn nhất để vật đi được quãng đường có độ dài A là
A.T/ 6 B.T/4 C.T/3 D.T/8
Hướng dẫn
Thời gian ngắn nhất để vật đi được quãng đường có độ dài A
\[\Rightarrow \]Lúc này vật đi từ vị trí có li độ \[x=\frac{A}{2}\to x=\frac{-A}{2}\]hoặc ngược lại \[\Rightarrow {{t}_{\min }}=\frac{T}{12}+\frac{T}{12}=\frac{T}{6}\]
Chọn đáp án A
Câu 15: Một vật dao động điều hòa với chu kì T và biên độ A . Quãng đường vật đi được tối đa trong khoảng thời gian 5T/3 là
A. 3A B. 5A C. 6,5A D. 7A
Hướng dẫn
Ta có: \[\frac{5T}{3}=T+\frac{T}{2}+\frac{T}{6}\]
Quãng đường vật đi được trong thời gian 1,5T là 6A
Quãng đường lớn nhất vật đi được trong thời gian T/6 là A.
Quãng đường vật đi được tối đa trong khoảng thời gian 5T/3 là 7A.
Chọn đáp án D







