A. Tóm tắt lý thuyết
Cho hai điểm cố định F1,F2 với F1F2=2c (c>0) v số 2a (2a >2c>0). Elíp (E) là tập hợp các điểm M sao cho MF1+MF2=2a
(E) : = {M : MF1+MF2=2a }.
Với F1F2=2c gọi là tiêu cự của (E).
2. Phương trình chính tắc của (E).

- Trục lớn A1A2=2a (nằm trên trục Ox)
- Trục nhỏ : B1B2=2b ( nằm trên trục Oy )
- Có bốn đỉnh : A1(-a;0) ,A2(a;0) B1(0;-b) và B2(0;b).
- Có hai tiêu điểm : F1(-c;0) và F2 (c;0 )
- Có tâm sai : $e=\frac{c}{a}=\frac{\sqrt{{{a}^{2}}-{{b}^{2}}}}{a}$
Phương trình hình chữ nhật cơ sở : x=±a và y=±b .
-Có hai bán kính qua tiêu : $M{{F}_{1}}=a-\frac{cx}{a};M{{F}_{2}}=a+\frac{cx}{a}$
3. Phương trình tiếp tuyến của Elip
a) Cho điểm M(x0;y0) thuộc (E ),thì tiếp tuyến của (E) tại M có phương trình là : 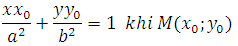
b) Điều kiện cần và đủ để đường thẳng : Ax+By+c=0 là tiếp tuyến (E) :
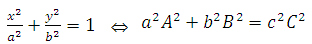
B.Một số dạng toán thường gặp
1. Dạng định hình :( Lập phương trình (E) khi cho biết một số điều kiện cho sẵn - Vẽ (E) khi biết phương trình của nó ).
Phương pháp giải :
a) Nếu lập phương trình (E).
- Dựa vào lý thuyết đã học ,thiết lập các phương trình sao cho tính được a,b ,sau đó thay vào phương trình chính tắc của (E)
- Dựa vào tính chất của (E) : ( Định nghĩa về (E) để thiết lập phương trình .
b) Để vẽ một (E) khi biết phương trình của nó :
- Vẽ hai trục toạ độ ,chia khoảng ( căn cứ vào giá trị của hai bán trục )
- Tìm vị trí của bốn đỉnh của (E)trên mặt phẳng toạ độ
- Vẽ hình chữ nhật cơ sở của (E)
- Vẽ (E) tiếp xúc với bốn cạnh của hình chữ nhật cơ sở của (E)
2. Dạng định tính : ( Tính toán - Giao của (E) với một đường thẳng - Tìm điểm nào đó có quan hệ với (E) đồng thời thoả mãn tính chất cho sẵn - Lập phương trình tiếp tuyến của (E)- Chứng minh một số tính chất của (E).....)
*Một số tính chất có được của (E)
- Với một điểm M bất kỳ thuộc (E) đều nhìn hai tiêu điểm của nó một góc vuông ( Có nghĩa là góc F1MF2= 90 độ ).
- Hai đường thẳng vuông góc nhau cùng đi qua gốc toạ độ O sẽ cắt (E) tại bốn điểm tạo thành một hình thoi .Hình thoi này ngoại tiếp một đường tròn có bán kính không đổi
- Tiếp tuyến của (E) tại một điểm M bất kỳ (nằm trên (E) ) là đường phân giác ngoài của góc F1MF2 .
- Tâm của đường tròn bàng tiếp của góc M ( của tam giác F1MF2 ) là giao của đường phân giác trong của góc M và hai đường phân giác của hai góc ngoài của hai góc ( MF1Ox) và góc (MF2Ox).
- Tỷ số khoảng cách từ một điểm nằm trên(E) tới đường chuẩn của (E)và đến một tiêu điểm ứng với đường chuẩn đó là một số không đổi .
* Một số ví dụ minh hoạ để học sinh tham khảo
Ví dụ 1. ( Bài 61-tr 111-BTHH10-NC)
Lập phương trình chính tắc của (E) biết
a) Một đỉnh A(0;-2) và một tiêu điểm F(1;0)
b) F1(-7;0) và (E) đi qua điểm M(-2;12)
c) Tiêu cự bằng 6 và có tâm sai e= 2/3.
d) Phương trình các cạnh của hình chữ nhật cơ sở : x=±4 và y=±3 .
e) (E) qua hai điểm M(4;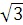 ) và N(
) và N(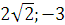 ).
).
Đáp số :
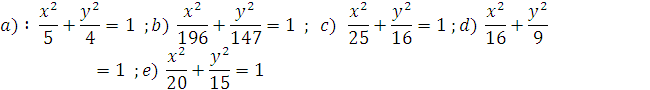
Ví dụ 2 .Viết phương trình chính tắc của (E) biết
a) Độ dài trục lớn bằng 6 và tiêu cự bằng 4
b) Tiêu điểm F1(-2;0) và độ dài trục lớn bằng 10
c) Tiêu điểm F1( -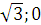 ) và đi qua điểm M(1;
) và đi qua điểm M(1;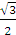 )
)
d) Qua hai điểm M(1;0) và N(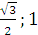 )
)
Đáp số :
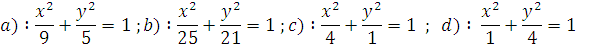
Ví dụ 3.( Bài 64-tr111-BTHH10-NC)
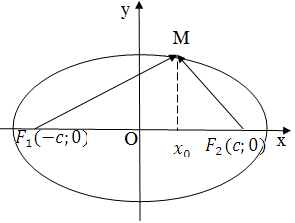
Cho (E) : 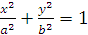 . (a>b>0 ). Gọi F1,F2 là tiêu điểm của (E) và A1,A2 là hai đỉnh của trục lớn .M là một điểm bất kỳ thuộc (E) có hình chiéu vuông góc trên trục Ox là H . Chứng minh rằng :
. (a>b>0 ). Gọi F1,F2 là tiêu điểm của (E) và A1,A2 là hai đỉnh của trục lớn .M là một điểm bất kỳ thuộc (E) có hình chiéu vuông góc trên trục Ox là H . Chứng minh rằng :
a) MF1.MF2+OM2=a2+b2 ;
b) (MF1-MF2)2=4(OM2-b2) ;
c) HM2=-b2/a2 . 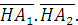
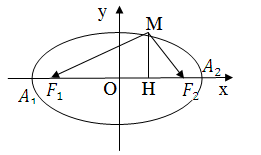
Bài giải :
a) Ta có : MF1= a-ex và MF2=a+ex , suy ra MF1.MF2=(a-ex)(a+ex)= a2-e2x2 (1).
Mặt khác : OM2=x2+y2 . Cho nên :
MF1.MF2+OM2= a2-e2x2+x2+y2 = a2+x2(1-e2)+y2 =a2+x2(1-c2/a2)+y2
= a2+x2-x2.(a2-b2)/a2+y2 = a2+x2-x2+b2(x2/a2+y2/b2)=a2+b2.
b) Ta có :
[MF1-MF2]2= [(a-ex)-(a+ex)]2=4e2x2 (1)
4(OM2-b2)=4(x2+y2-b2)= 4[ x2+b2(1-x2/a2)-b2]=4[x2-(a2-c2)x2/a2]=4e2x2 =(1)
c) Ta có :
-b2/a2 . 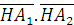 =-b2/a2.(-a-x)(a-x)=b2/a2(a2-x2)=b2(1- x2/a2)=y2= HM2 .
=-b2/a2.(-a-x)(a-x)=b2/a2(a2-x2)=b2(1- x2/a2)=y2= HM2 .
Ví dụ 4. (Bài 63-tr111-BTHH10-NC)
Tìm những điểm trên (E) : 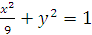 . Thoả mãn
. Thoả mãn
a) Có bán kính tiêu điểm trái bằng hai lần bán kính qua tiêu điểm phải
b) Nhìn hai tiêu điểm dưới một góc vuông
c) Nhìn hai tiêu điểm dưới một góc 600 ?
Bài giải :
a) Gọi M(x0;y0) thuộc (E): 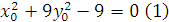
Mặt khác : Theo công thức tính bán kính qua tiêu thì MF1=a-ex0 và MF2=a+ex0 .Vì vậy , nếu MF1=2MF2 thì : a+ex0=2(a-ex0) Suy ra : x0=a/3e; Với e=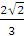

Vậy có hai điểm cần tìm M1(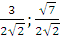 ) và M2(
) và M2(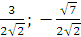 ).
).
b)Từ phương trình của (E) ,ta có : a=3 ,b=1 và e=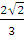 ,c=2
,c=2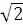 . Gọi M(x;y) bất kỳ thuộc (E),thì :
. Gọi M(x;y) bất kỳ thuộc (E),thì : 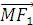 =(x+c; y) ;
=(x+c; y) ; 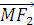 =(x-c; y) . Cho nên nếu M nhìn hai tiêu điểm dưới một góc vuông thì
=(x-c; y) . Cho nên nếu M nhìn hai tiêu điểm dưới một góc vuông thì 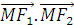 =0 . Hay
=0 . Hay 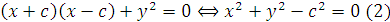
Kết hợp với phương trình (1) ta có hệ
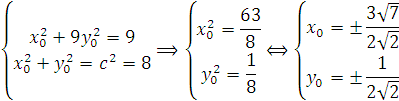
Vậy có bốn điểm cần tìm ( ).
).
c) Ta có :
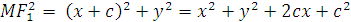
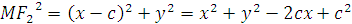
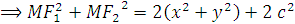
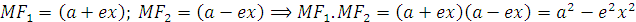
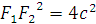
Do đó nếu M nhì hai tiêu điểm dưới một góc 600 thì theo hệ thức hàm số cos áp dụng cho tam giác F1MF2,ta thu được kết quả sau :
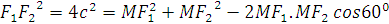
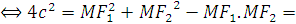
Hoặc :
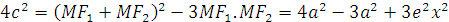
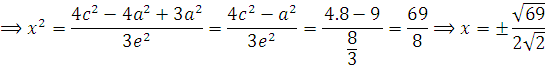
Vì M thuộc (E) :
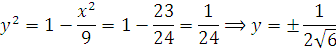
Vậy có 4 điểm thoả mãn : (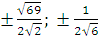 ).
).
Ví dụ 5 (Bài 66-tr112-BTHH10-NC).
Cho (E) líp có phương trình : : 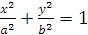 . (a>b>0)
. (a>b>0)
a) Chứng minh rằng với mọi M thuộc (E)ta luôn có b≤OM≤a
b) Gọi A là giao điểm của đường thẳng có phương trình mx +ny =0 với (E) .Tính OA theo a,b,m,n ?
b) Gọi B là điểm trên (E) sao cho OB vuông góc với OA . Chứng minh rằng tổng 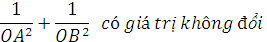
c) Chứng minh rằng đường thẳng AB luôn tiếp xúc với một đường tròn cố định ?
Bài giải :
a) Vì a>b>0 .Cho nn nếu M(x0;y0) thuộc (E)
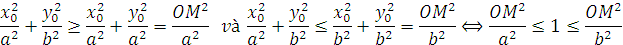
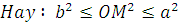
b) Đường thẳng (d) : mx+ny=0 cắt (E) tai hai điểm A,E có toạ độ là nghiệm của hệ :
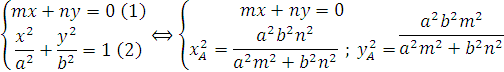
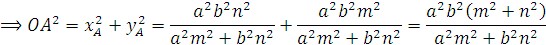
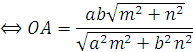
c) Do OA vuông góc với OB ,nên đường thẳng (OB): nx-my=0 . Vậy (OB) cắt (E) tại B ( Với : nx+(-m)y=0 ) cho nên trong toạ độ của A ta chỉ thay m thành n và n thay bằng (-m)
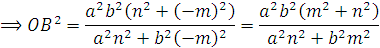

* Nếu kẻ OH vuông góc với AB thì theo tính chât của tam giác vuông ta có :
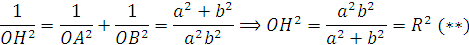
Vậy đường thẳng AB luôn tiếp xúc với đường tròn cố định với bàn kính R xác định theo (**)
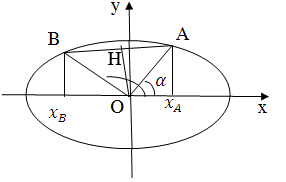
* Chú ý bài tập trên ở câu c) còn có một cách hỏi khác :
- Tìm trên (E) hai điểm A và B sao cho OA vuông góc với OB
Khi đó ta còn có cách giải khác :
Gọi 
 là góc tạo bởi OA với chiều dương của Ox. Nếu OB vuông góc với OA thì góc giữa OA và chiều dương của Ox là 900-
là góc tạo bởi OA với chiều dương của Ox. Nếu OB vuông góc với OA thì góc giữa OA và chiều dương của Ox là 900-
 .
.
Ta có :
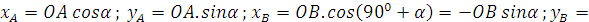
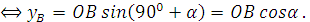
Từ đó ta có kết quả sau :Do A thuộc (E) :
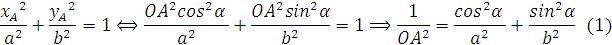
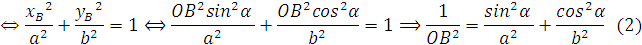
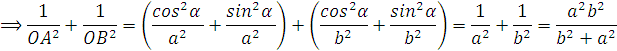
Kết quả giống như ta giải ở trên.
- Hai đường thẳng vuông góc với nhau có phương trình : mx+ny=0 và nx-my=0 cắt (E) tai bốn điểm A,B,C và D tạo thành một hình thoi
a) Tính diện tích của hình thoi theo a,b,m,n ?
b) Hãy tìm điều kiện của m,n để diện tích của hình thoi đạt GTLN ?
* Học sinh hãy thử sức mình xem sao ?
* Gợi ý : Theo kết quả bài trên thì diện tích của hình thoi bằng 4 lần diện tích của tam giác OAB,có nghĩa là
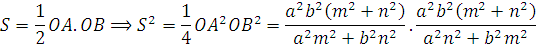
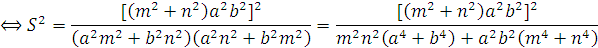
Do 
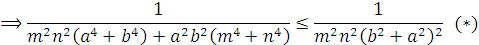
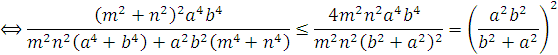
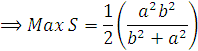
Ví dụ 6. (Bài 65-tr112-BTHH10-NC).
Cho (E) : 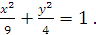
a) Tìm toạ độ các đỉnh ,tính tâm sai và vẽ (E).
b) Xác định đường thẳng (d) : y=x+m (m là tham số ) có điểm chung với (E)?
c) Viết phương trình của (d') đi qua M(1;1) và cắt (E) tại hai điểm A,B sao cho M là trung điểm của AB ?
Bài giải :
a) (E) có a=3 ; b=2 ; c2=a2-b2=9-4=5 ,do đó  .
.
b) Đường thẳng (d) cắt (E) tại hai điểm A,B có toạ độ là nghiệm của hệ :
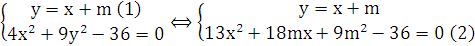
Để tồn tại hai nghiêm :
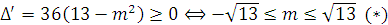
c) Gọi véc tơ chỉ phương của (d') đi qua M(1;1) với toạ độ (a,b) ,thì (d') có phương trình là 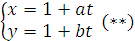 . Nếu (d') cát (E) tại hai điểm A,B thì toạ độ của AB là nghiệm của hệ
. Nếu (d') cát (E) tại hai điểm A,B thì toạ độ của AB là nghiệm của hệ
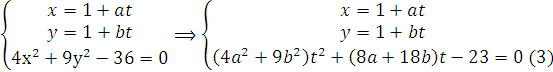
Do A,B thuộc (d') ,nên 
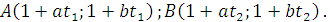 Với t1,t2 là hai nghiệm của phương trình (3) .
Với t1,t2 là hai nghiệm của phương trình (3) .
Nếu M là trung điểm của AB thì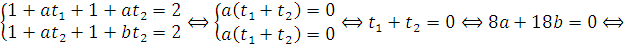
Ta chọn a=9 và b=-4 ,thì (d') có phương trình là :4x+9y-13=0 .







