bài tập số phức

Giả sử ${{z}_{1}},{{z}_{2}}$ là hai nghiệm phức của phương trình  \[\left| \left( 2+i \right)\left| z \right|z-(1-2i)z \right|=\left| 1+3i \right|\] và $\left| {{z}_{1}}-{{z}_{2}} \right|=1$. Tính $M=\left| 2{{z}_{1}}+3{{z}_{2}} \right|$

Cho các số phức \[{{z}_{1}}=-3i,{{z}_{2}}=4+i\] và z thỏa mãn \[\left| z-i \right|=2.\] Biết biểu thức \[T=\left| z-{{z}_{1}} \right|+2\left| z-{{z}_{2}} \right|\] đạt giá trị nhỏ nhất khi \[z=a+bi\left( a;b\in R \right).\] Hiệu \[a-b\] bằng:

Cho hai số phức z, w thỏa mãn 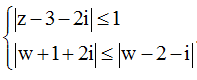 Tìm giá trị nhỏ nhất ${{P}_{\min }}$của biểu thức $P=\left| z-w \right|$.

Cho số phức z thỏa mãn điều kiện $\left| z-1 \right|=\sqrt{2}$. Tìm giá trị lớn nhất của biểu thức $T=\left| z+i \right|+\left| z-2-i \right|$ 

Cho số phức z thỏa mãn $5\left| z-i \right|=\left| z+1-3i \right|+3\left| z-1+i \right|.$ Tìm giá trị lớn nhất M của \[\left| z-2\text{+}3i \right|?\] 

Trong tập các số phức, gọi ${{z}_{1}},{{z}_{2}}$ là hai nghiệm của phương trình ${{z}^{2}}-z+\frac{2017}{4}=0$ với ${{z}_{2}}$ có thành phần ảo dương. Cho số phức z thỏa mãn $\left| z-{{z}_{1}} \right|=1$ Giá trị nhỏ nhất của $P=\left| z-{{z}_{2}} \right|$ là:

Cho số phức $z=1+i$. Biết rằng tồn tại các số phức ${{z}_{1}}=a+5i,\,\,{{z}_{2}}=b$ (trong đó $a,b\in \mathbb{R},\,b>1$) thỏa mãn $\sqrt{3}\left| z-{{z}_{1}} \right|=\sqrt{3}\left| z-{{z}_{2}} \right|=\left| {{z}_{1}}-{{z}_{2}} \right|$. Tính $b-a$.    

Cho số phức z thỏa mãn \[\left| z-3-4i \right|=\sqrt{5}.\] Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức$P={{\left| z+2 \right|}^{2}}+-{{\left| z-i \right|}^{2}}.$ Tính môđun của số phức \[\text{w}=M+mi.\] 

Cho các số phức ${{z}_{1}}=1,{{z}_{2}}=2-3i$ và số phức $z$ thỏa mãn $\left| z-1-i \right|+\left| z-3+i \right|=2\sqrt{2}$. Gọi $M,m$ lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của $P=\left| z-{{z}_{1}} \right|+\left| z-{{z}_{2}} \right|$. Tính tổng $S=M+m$?  

Cho số phức z thỏa mãn $\left| z-2+3i \right|+\left| z-2+i \right|=4\sqrt{5}.$ Tính GTLN của $P=\left| z-4+4i \right|$ 

Cho i là đơn vị ảo. Gọi S là tập hợp các số nguyên dương n có 2 chữ số thỏa mãn ${{i}^{n}}$ là số nguyên dương. Số phần tử của S là:

Cho các số phức $z$ thỏa mãn $\left| z \right|=1$. Gọi $M,\,m$ lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức $P=\left| z+1 \right|+\left| {{z}^{2}}+3z+2 \right|$. Tỉ số $\frac{M}{m+2}$ là 

Xét các số phức \[z=a+bi,\left( a,b\in \mathbb{R} \right)\]  thỏa mãn $\left| z-1+2i \right|=\sqrt{5}.$

Tìm P= 16a+8b  biết $\left| z+1+i \right|+\left| z-1+4i \right|$ đạt giá trị lớn nhất.

Cho hai số phức ${{z}_{1}},{{z}_{2}}$ thỏa mãn $\left| {{z}_{1}} \right|=2,\left| {{z}_{2}} \right|=\sqrt{3}.$ Gọi M, N là các điểm biểu diễn cho ${{z}_{1}}$ và $i{{z}_{2}}.$ Biết $MON={{30}^{0}}.$ Tính $S=\left| z_{1}^{2}+4z_{2}^{2} \right|?$

Cho số  phức z thỏa mãn $4\left| z+i \right|+3\left| z-i \right|=10.$  Giá trị nhỏ nhất của $\left| z \right|$ bằng: