hưng việt 01

Cho hai số phức z, w thỏa mãn 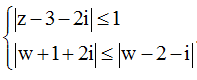 Tìm giá trị nhỏ nhất ${{P}_{\min }}$của biểu thức $P=\left| z-w \right|$.

Cho i là đơn vị ảo. Gọi S là tập hợp các số nguyên dương n có 2 chữ số thỏa mãn ${{i}^{n}}$ là số nguyên dương. Số phần tử của S là:

Cho số phức z thỏa mãn $\left| z-2+3i \right|+\left| z-2+i \right|=4\sqrt{5}.$ Tính GTLN của $P=\left| z-4+4i \right|$ 

Cho số phức z thỏa mãn \[\left| z-3-4i \right|=\sqrt{5}.\] Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức$P={{\left| z+2 \right|}^{2}}+-{{\left| z-i \right|}^{2}}.$ Tính môđun của số phức \[\text{w}=M+mi.\] 

Cho số phức z và w thỏa mãn $z+\text{w}=3+4i$ và $\left| z-\text{w} \right|=9.$ Tìm giá trị lớn nhất của biểu thức $T=\left| z \right|+\left| \text{w} \right|$. 

Trong tập các số phức, gọi ${{z}_{1}},{{z}_{2}}$ là hai nghiệm của phương trình ${{z}^{2}}-z+\frac{2017}{4}=0$ với ${{z}_{2}}$ có thành phần ảo dương. Cho số phức z thỏa mãn $\left| z-{{z}_{1}} \right|=1$ Giá trị nhỏ nhất của $P=\left| z-{{z}_{2}} \right|$ là:

Cho các số phức $z$ thỏa mãn $\left| z \right|=1$. Gọi $M,\,m$ lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức $P=\left| z+1 \right|+\left| {{z}^{2}}+3z+2 \right|$. Tỉ số $\frac{M}{m+2}$ là 

Với hai số phức ${{z}_{1}}$ và ${{z}_{2}}$ thỏa mãn ${{z}_{1}}+{{z}_{2}}=8+6i$ và $\left| {{z}_{1}}-{{z}_{2}} \right|=2,$ tìm giá trị lớn nhất $P=\left| {{z}_{1}} \right|+\left| {{z}_{2}} \right|$.

Cho số phức $z$ thỏa mãn $\left| z-1 \right|=\left| z-i \right|$. Tìm mô đun nhỏ nhất của số phức\[\text{w}=2z+2-i\].            

Xét các số phức \[z=a+bi,\left( a,b\in \mathbb{R} \right)\]  thỏa mãn $\left| z-1+2i \right|=\sqrt{5}.$

Tìm P= 16a+8b  biết $\left| z+1+i \right|+\left| z-1+4i \right|$ đạt giá trị lớn nhất.

Cho hàm số \[y=f\left( x \right)\]có đồ thị như hình vẽ bên

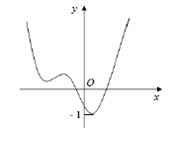
Tìm số điểm cực trị của hàm số \[y={{2}^{f\left( x \right)}}-{{3}^{f\left( x \right)}}\]

Tìm tập hợp S tất cả các giá trị của tham số m để đồ thị hàm số \[y={{x}^{4}}-2{{m}^{2}}{{x}^{2}}+{{m}^{4}}+3\] có ba điểm cực trị đồng thời ba điểm cực trị đó cùng với gốc tọa độ O tạo thành tứ giác nội tiếp.

Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [0;2018] để hệ phương trình    có nghiệm ?

Tìm tất cả các giá trị của m để hàm số $y=-x^3-3x^2+4mx-2$ nghịch biến trên $(-\infty ;0]$

Cho hàm số$y=f\left( x \right)$ có đạo hàm$f'\left( x \right)={{x}^{2}}\left( x-1 \right){{\left( x-4 \right)}^{2}}$. Khi đó số điểm cực trị của hàm số$y=f\left( {{x}^{2}} \right)$ là

Biết đồ thị hàm số $f\left( x \right)=a\,{{x}^{3}}+b{{x}^{2}}+cx+d$ cắt trục hoành tại ba điểm phân biệt có hoành độ lần lượt là ${{x}_{1}},{{x}_{2}},{{x}_{3}}.$ Tính giá trị của biểu thức $T=\frac{1}{f'\left( {{x}_{1}} \right)}+\frac{1}{f'\left( {{x}_{2}} \right)}+\frac{1}{f'\left( {{x}_{3}} \right)}.$

Cho hàm số $y=f\left( x \right)$có bảng biến thiên như sau.

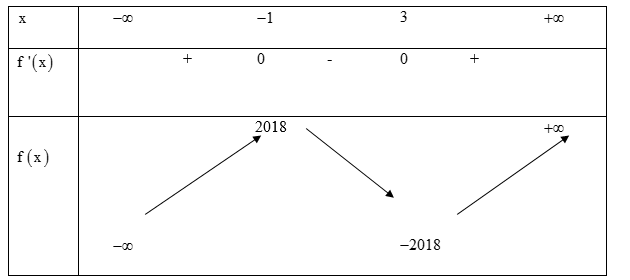
Đồ thị hàm số \[y=\left| f\left( \text{x}-2017 \right)+2018 \right|\] có bao nhiêu điểm cực trị?

Cho đồ thị của ba hàm số $y=f\left( x \right),y=f'\left( x \right),y=f''\left( x \right)$ được  mô tả bằng hình vẽ. Hỏi đồ thị của các hàm số $y=f\left( x \right),y=f'\left( x \right),y=f''\left( x \right)$ theo thứ tự, lần lượt tương ứng với đường cong nào?

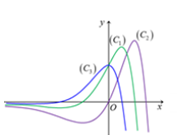
Cho hàm số $y=\frac{{{x}^{3}}}{3}-a{{x}^{2}}-3ax+4.$ Để hàm số đạt cực trị tại ${{x}_{1}};{{x}_{2}}$ thỏa mãn $\frac{x_{1}^{2}+2a{{x}_{2}}+9a}{{{a}^{2}}}+\frac{x_{2}^{2}+2a{{x}_{1}}+9a}{{{a}^{2}}}=2$ thì a thuộc khoảng nào ?

Cho $f\left( x \right)=\left( {{m}^{4}}+1 \right){{x}^{4}}+\left( -{{2}^{m+1}}.{{m}^{2}}-4 \right){{x}^{2}}+{{4}^{m}}+16,m\in \mathbb{R}.$ Số cực trị của hàm số $y=\left| f\left( x \right)-1 \right|$ là:

Cho x, y là các số thực thỏa mãn điều kiện ${{3}^{{{x}^{2}}+{{y}^{2}}-2}}.{{\log }_{2}}\left( x-y \right)=\frac{1}{2}\left[ 1+{{\log }_{2}}\left( 1-xy \right) \right].$ Tìm giá trị lớn nhất của biểu thức $M=2\left( {{x}^{3}}+{{y}^{3}} \right)-3xy.$ 

 Cho hàm số \[f\left( x \right)=\ln \left( 1-\frac{1}{{{x}^{2}}} \right).\] Biết rằng \[f\left( 2 \right)+f\left( 3 \right)+...+f\left( 2018 \right)=\ln a-\ln b+\ln c-\ln d\] với a, b, c, d là các số nguyên dương, trong đó a, c, d là các số nguyên tố và \[a

Cho hai số thực x,y thỏa mãn $0\le x\le \frac{1}{2},\,0

Số  các  giá  trị  nguyên  của  tham  số  m  để  phương  trình ${{\log }_{\sqrt{2}}}\left( x-1 \right)={{\log }_{2}}\left( mx-8 \right)$ có hai nghiệm thực phân biệt là :

Cho hai số dương x,y thỏa mãn ${{\log }_{2}}{{\left( 4x+y+2xy+2 \right)}^{y+2}}=8-(2x-2)(y+2)$ . Giá trị nhỏ nhất $P=2x+y$ là số có dạng $M=a\sqrt{b}+c$ với $a;b\in N,a>2$ . Tính $S=a+b+c$

Cho $f\left( x \right)={{e}^{\sqrt{1+\frac{1}{{{x}^{2}}}+\frac{1}{{{\left( x+1 \right)}^{2}}}}}}.$ Biết rằng \[f\left( 1 \right).f\left( 2 \right).f\left( 3 \right)...f\left( 2017 \right)={{e}^{\frac{m}{n}}}\] với m, n là các số tự nhiên và $\frac{m}{n}$  là phân số tối giản. Tính $m-{{n}^{2}}.$

Có bao nhiêu số nguyên m thuộc đoạn $\left[ -50;50 \right]$ sao cho phương trình ${{\log }_{\sqrt{2}}}\left( m\text{x}-6{{\text{x}}^{2}} \right)-2{{\log }_{2}}\left( -14{{\text{x}}^{2}}+29\text{x}-2 \right)=0$ có nghiệm duy nhất ?

Cho hàm số $y=f\left( x \right)=2018\ln \left( {{e}^{\frac{x}{2018}}}+\sqrt{e} \right).$ Tính giá trị biểu thức $T=f'\left( 1 \right)+f'\left( 2 \right)+...+f'\left( 2017 \right).$

Tìm tất cả các giá trị thực của tham số \[a\left( a>0 \right)\] thỏa mãn \[{{\left( {{2}^{a}}+\frac{1}{{{2}^{a}}} \right)}^{2017}}\le {{\left( {{2}^{2017}}+\frac{1}{{{2}^{2017}}} \right)}^{a}}\]

Gọi \[x,y\] là các số thực dương thỏa mãn điều kiện \[{{\log }_{9}}x={{\log }_{6}}x={{\log }_{4}}(x+y)\] và \[\frac{x}{y}=\frac{-a+\sqrt{b}}{2}\], với \[a,b\] là hai số nguyên dương. Tính \[a+b\].

Cho hàm số $f\left( x \right)$có đạo hàm liên tục trên đoạn $\left[ 0;1 \right]$thỏa mãn $f\left( 1 \right)=1;\int\limits_{0}^{1}{{{\left[ f'\left( x \right) \right]}^{2}}dx}=9$ và $\int\limits_{0}^{1}{{{x}^{3}}f\left( x \right)dx=\frac{1}{2}.}$ Tích phân $\int\limits_{0}^{1}{f\left( x \right)dx}$bằng :

Cho hàm số $f\left( x \right)$ xác định trên $\mathbb{R}\backslash \left\{ -2;1 \right\}$ thỏa mãn $f'\left( x \right)=\frac{1}{{{x}^{2}}+x-2},f\left( -3 \right)-f\left( 3 \right)=0$ và $f\left( 0 \right)=\frac{1}{3}.$ Giá trị biểu thức $f\left( -4 \right)+f\left( -1 \right)-f\left( 4 \right)$ bằng:

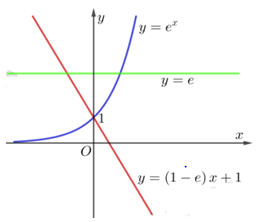
Cho $\left( H \right)$ là hình phẳng giới hạn bởi các đồ thị hàm số $y=e,y={{e}^{x}}$ và $y=\left( 1-e \right)x+1$ (tham khảo hình vẽ). Diện tích của $\left( H \right)$là

Cho hàm số $y=f\left( x \right)$ liên tục trên đoạn $\left[ 0;1 \right]$ và thỏa mãn $f\left( x \right)-8{{x}^{3}}f\left( {{x}^{4}} \right)+\frac{{{x}^{3}}}{\sqrt{{{x}^{2}}+1}}=0$. Tích phân $I=\int\limits_{0}^{1}{f\left( x \right)dx}$ có kết quả dạng $\frac{a-b\sqrt{2}}{c}$ với $a,b,c\in \mathbb{R}$, $\frac{a}{c},\frac{b}{c}$ tối giản. Tính $a+b+c$.   

Cho hàm số \[f\left( x \right)\] có đạo hàm và liên tục trên đoạn \[\left[ 4;8 \right]\] và \[f\left( x \right)\ne 0\forall x\in \left[ 4;8 \right].\] Biết rằng \[\int\limits_{4}^{8}{\frac{{{\left[ f'\left( x \right) \right]}^{2}}}{{{\left[ f\left( x \right) \right]}^{4}}}dx}=1\] và \[f\left( 4 \right)=\frac{1}{4},f\left( 8 \right)=\frac{1}{2}.\] Tính \[f\left( 6 \right).\]

Cho hàm số $y=f(x)$ nghịch biến trên R và thỏa mãn $\left[ f(x)-x \right]f(x)={{x}^{6}}+3{{x}^{4}}+2{{x}^{2}},\forall x\in R$ . Giá trị $I=\int\limits_{1}^{2}{f(x)dx}$ bằng bao nhiêu?

Cho biết $\int\limits_{0}^{\frac{\pi }{4}}{\frac{\text{cos}x}{\operatorname{s}\text{inx}+c\text{osx}}dx=a\pi +b\ln 2}$ với $a\,$và $b$ là các số hữu tỉ. Khi đó \[\frac{a}{b}\] bằng:

Cho hàm số $f\left( x \right)$ có đạo hàm không âm trên \[[0;1]\] thỏa mãn ${{\left[ f\left( x \right) \right]}^{4}}{{\left[ f'\left( x \right) \right]}^{2}}\left( {{x}^{2}}+1 \right)=1+{{\left[ f\left( x \right) \right]}^{3}}$ và $f\left( x \right)>0$ với \[\forall x\in [0;1],\] biết $f\left( 0 \right)=2.$  f(1) nằm trong khoảng nào trong các khoảng sau:

Giá trị của tích phân \[\int_{0}^{100}{x\left( x-1 \right)...\left( x-100 \right)dx}\] bằng

Cho hàm số $f\left( x \right)$ có đạo hàm dương, liên tục trên đoạn $\left[ 0;1 \right]$ thỏa mãn điều kiện $f\left( 0 \right)=1$ và $3\int\limits_{0}^{1}{\left[ f'\left( x \right).{{\left[ f\left( x \right) \right]}^{2}}+\frac{1}{9} \right]}\,dx\le 2\int\limits_{0}^{1}{\sqrt{f'\left( x \right)}.f\left( x \right)dx.}$ Tính $\int\limits_{0}^{1}{{{\left[ f\left( x \right) \right]}^{3}}dx.}$

Một công ty muốn thiết kế bao bì để đựng sữa với thể tích $1d{{m}^{3}}$. Bao bì được thiết kế bởi một trong hai mô hình sau: dạng hình hộp chữ nhật có đáy là hình vuông hoặc dạng hình trụ và được sản xuất cùng một nguyên vật liệu. Hỏi thiết kế theo mô hình nào sẽ tiết kiệm được nguyên vật liệu nhất? Và thiết kế mô hình đó theo kích thước như thế nào?

Một người mua một căn hộ với giá 900 triều đồng. Người đó trả trước với số tiền là 500 triệu đồng. Số tiền còn lại người đó thanh toán theo hình thức trả góp với lãi suất tính trên tổng số tiền còn nợ là 0,5% mỗi tháng. Kể từ ngày mua, sau đúng mỗi tháng người đó trả số tiền cố định là 4 triệu đồng (cả gốc lẫn lãi). Tìm thời gian (làm tròn đến hàng đơn vị) để người đó trả hết nợ.

Ông An muốn xây một cái bể chứa nước lớn dạng một khối hộp chữ nhật không nắp có thể tích bằng \[288{{m}^{3}}\] Đáy bể là hình chữ nhật có chiều dài gấp đôi chiều rộng, giá thuê nhân công để xây bể là 500000 đồng/\[{{m}^{2}}\]. Nếu ông An biết xác định các kích thước của bể hợp lí thì chi phí thuê nhân công sẽ thấp nhất. Hỏi ông An trả chi phí thấp nhất để xây dựng bể đó là bao nhiêu?

Thầy Tâm cần xây một hồ chứa nước với dạng khối hộp chữ nhật không nắp có thể tích bằng $\frac{500}{3}{{m}^{3}}$. Đáy hồ là hình chữ nhật có chiều dài gấp đôi chiều rộng. Giá thuê nhân công để xây hồ là 500.000 đồng/${{m}^{2}}$. Khi đó, kích thước của hồ nước như thể nào để chi phí thuê nhân công mà thầy Tâm phải trả thấp nhất:

Có một bể hình hộp chữ nhật chứa đầy nước. Người ta cho ba khối nón giống nhau có thiết diện qua trục là một tam giác vuông cân vào bể sao cho ba đường tròn đáy của ba khối nón tiếp xúc với nhau, một khối nón có đường tròn đáy chỉ tiếp xúc với một cạnh của đáy bể và hai khối nón còn lại có đường tròn đáy tiếp xúc với hai cạnh của đáy bể. Sau đó người ta đặt lên đỉnh của ba khối nón một khối cầu có bán kính bằng $\frac{4}{3}$ lần bán kính đáy của khối nón. Biết khối cầu vừa đủ ngập trong nước và lượng nước trào ra là $\frac{337\pi }{3}\left( c{{m}^{3}} \right).$ Tính thể tích nước ban đầu ở trong bể.

Trò chơi quay bánh xe số trong chương trình truyền hình “Hãy chọn giá đúng” của kênh VTV3 Đài truyền hình Việt Nam, bánh xe số có 20 nấc điểm: 5, 10, 15,…., 100 với vạch chia đều nhau và giả sử rằng khả năng chuyển từ nấc điểm đã có tới các nấc điểm còn lại là như nhau.

Trong mỗi lượt chơi có 2 người tham gia, mỗi người được quyền chọn quay 1 hoặc 2 lần, và điểm số của người chơi được tính như sau:

  + Nếu người chơi chọn quay 1 lần thì điểm của người chơi là điểm quay được.

  + Nếu người chơi chọn quay 2 lần và tổng điểm quay được không lớn hơn 100 thì điểm của người chơi là tổng điểm quay được.

  + Nếu người chơi chọn quay 2 lần và tổng điểm quay được lớn hơn 100 thì điểm của người chơi là tổng điểm quay được trừ đi 100.

Luật chơi quy định, trong mỗi lượt chơi người nào có điểm số cao hơn sẽ thắng cuộc, hòa nhau sẽ chơi lại lượt khác.

An và Bình cùng tham gia một lượt chơi, An chơi trước và có điểm số là 75. Tính xác suất để Bình thắng cuộc ngay ở lượt chơi này.

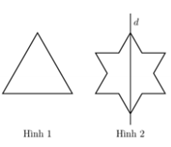
Ban đầu ta có một tam giác đều cạnh bằng 3 (hình 1). Tiếp đó ta chia mỗi cạnh của tam giác thành 3 đoạn bằng nhau và thay mỗi đoạn ở giữa bởi hai đoạn bằng nó sao cho chúng tạo với đoạn bỏ đi một tam giác đều về phía ngoài ta được hình 2. Khi quay hình 2 xung quanh trục d ta được một khối tròn xoay. Tính thể tích khối tròn xoay đó.

Trong năm đầu tiên đi làm, anh A được nhận lương là 10 triệu đồng mỗi tháng. Cứ  hết một năm, anh A lại được tăng lương, mỗi tháng sau tăng 12% so với mỗi tháng trước. Mỗi khi lĩnh lương anh A đều cất đi phần lương tăng so với năm ngay trước để  tiết kiệm mua ô tô. Hỏi sau ít nhất bao nhiêu năm đi làm thì anh A mua được ô tô giá 500 triệu biết rằng anh được gia đình hỗ trợ 32% giá trị chiếc xe.

Người ta cần xây một hồ chứa nước với dạng khối hộp chữ nhật không nắp có thể tích bằng

m³. Đáy hồ là hình chữ nhật có chiều dài gấp đôi chiều rộng. Giá thuê nhân công để xây hồ là 500.000 đồng/m². Khi đó, kích thước của hồ nước sao cho chi phí thuê nhân công thấp nhất là

 Người ta muốn xây một chiếc bể chứa nước có hình dạng là một khối hộp chữ nhật không nắp có thể tích bằng $\frac{500}{3}{{m}^{3}}.$ Biết đáy hồ là một hình chữ nhật có chiều dài gấp đôi chiều rộng và giá thuê thợ xây là 100.000 đồng $/{{m}^{2}}.$ Tìm kích thước của hồ để chi phí thuê nhân công ít nhất. Khi đó chi phí thuê nhân công là: