Bài Tập Điện Xoay Chiều Vận Dụng Cao (P1)

BÀI TẬP ĐIỆN XOAY CHIỀU VẬN DỤNG CAO (P1)

 

Hướng dẫn

Ta có: Khi L = L₁ thì U_AM1 = U_R1 = U Khi L = L₂ thì ${{U}_{AM2}}={{U}_{R2}}=\sqrt{8}U$

${{\varphi }_{1}}+{{\varphi }_{2}}=\frac{\pi }{2}\to \tan {{\varphi }_{1}}\tan {{\varphi }_{2}}=-1\to \frac{{{Z}_{L1}}-{{Z}_{C1}}}{R}.\frac{{{Z}_{L1}}-{{Z}_{C1}}}{R}=-1\left( 1 \right)$

Mặt khác: ta có:

\[\frac{{{U}_{R1}}}{{{U}_{R2}}}=\frac{1}{\sqrt{8}}\to {{I}_{2}}=\sqrt{8}{{I}_{1}}\to {{Z}_{1}}=\sqrt{8}{{Z}_{2}}\]

\[\leftrightarrow \sqrt{{{R}^{2}}+{{\left( {{Z}_{L1}}-{{Z}_{C}} \right)}^{2}}}=\sqrt{8}\sqrt{{{R}^{2}}+{{\left( {{Z}_{L2}}-{{Z}_{C}} \right)}^{2}}}\]

\[\leftrightarrow {{\left( {{Z}_{L1}}-{{Z}_{C}} \right)}^{2}}-7{{R}^{2}}-8{{\left( {{Z}_{L2}}-{{Z}_{C}} \right)}^{2}}=0\left( 2 \right)\]

Chia cả hai vế của (2) cho (Z_L2 - Z_C) kết hợp với (1), Ta được:

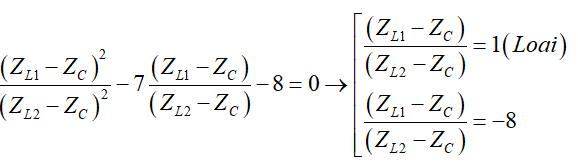
Với $\frac{\left( {{Z}_{L1}}-{{Z}_{C}} \right)}{\left( {{Z}_{L2}}-{{Z}_{C}} \right)}=-8\to -\frac{\left( {{Z}_{L1}}-{{Z}_{C}} \right)}{8}=\left( {{Z}_{L2}}-{{Z}_{C}} \right)$ Thay vào (1) $\Rightarrow {{\left( {{Z}_{L1}}-{{Z}_{C}} \right)}^{2}}=8{{R}^{2}}$

Hệ số công suất của mạch khi L=L: $\cos {{\varphi }_{1}}=\frac{R}{{{Z}_{1}}}=\frac{R}{\sqrt{{{R}^{2}}+{{\left( {{Z}_{L1}}-{{Z}_{C}} \right)}^{2}}}}=\frac{R}{3R}=\frac{1}{3}\Rightarrow $ Chọn A

 

Hướng dẫn

Công suất hao phí trên đường dây $\Delta P=\frac{{{P}^{2}}R}{{{U}^{2}}{{\cos }^{2}}\varphi }={{P}^{2}}x\,(x=\frac{R}{{{U}^{2}}{{\cos }^{2}}\varphi }$  không đổi)

Ban đầu: $\frac{\Delta P}{P}=Px=1-H=1-0,75=0,25$. Sau khi công suất sử dụng tăng lên 25%:

$P'-\Delta P'=1,25\left( P-\Delta P \right)=0,9375P\to P'-{{P}^{2}}$

$x=0,937P\to \frac{P'}{P}-{{P}^{2}}$

$P\frac{0,25}{P}=0,9375$ Đặt P’/P = m, ta có:

Với k = 2,5 $\Rightarrow H=1-\frac{\Delta P'}{P'}=1-P'x=1-2,5Px=0,375=37,5%$ (loại vì hao phí không quá 40%)

Với k = 1,5 $\Rightarrow H=1-\frac{\Delta P'}{P'}=1-P'x=1-1,5Px=0,625=62,5%\Rightarrow $ Chọn C

(loại vì hao phí không quá 40%)

 

Hướng dẫn

${{u}_{AN}}={{u}_{L}}+{{u}_{X}}{{u}_{MB}}={{u}_{C}}+{{u}_{X}}{{u}_{AB}}={{u}_{AN}}+{{u}_{C}}{{u}_{AB}}\ge OH\Rightarrow {{\left( {{U}_{AM}} \right)}_{\min }}=OH$

 

Áp dụng hệ thức lượng trong tam giác vuông ta có: $\frac{1}{U_{AB}^{2}}=\frac{1}{U_{AN}^{2}}+\frac{1}{U_{MB}^{2}}\Rightarrow {{U}_{AB}}=24V$

Hướng dẫn

\[\frac{U_{0}^{2}}{{{3}^{2}}}=R_{0}^{2}+Z_{L}^{2}\Rightarrow Z_{L}^{2}=\frac{U_{0}^{2}}{{{3}^{2}}}-5,76\]

\[\frac{U_{0}^{2}}{{{4}^{2}}}=R_{0}^{2}+{{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}\Rightarrow {{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}=\frac{U_{0}^{2}}{{{4}^{2}}}-5,76{{R}^{2}}={{Z}_{L}}\left( {{Z}_{L}}-{{Z}_{C}} \right)\]

\[\Rightarrow \frac{{{R}^{2}}}{Z_{L}^{2}}=\frac{{{Z}_{L}}-{{Z}_{C}}}{{{Z}_{L}}}\Rightarrow \frac{\frac{U_{0}^{2}}{{{4}^{2}}}-5,76}{\frac{U_{0}^{2}}{{{3}^{2}}}-5,76}{{\left( \frac{{{R}^{2}}}{Z_{L}^{2}} \right)}^{2}}\]

\[\Rightarrow \left( \frac{U_{0}^{2}}{{{4}^{2}}}-5,76 \right)\left( \frac{U_{0}^{2}}{{{3}^{2}}}-5,76 \right)={{R}^{4}}\left( \frac{U_{0}^{2}}{{{3}^{2}}}-5,76 \right)\]

\[\Rightarrow \left( \frac{U_{0}^{2}}{{{4}^{2}}}-5,76 \right)\left( \frac{U_{0}^{2}}{{{3}^{2}}}-5,76 \right)={{R}^{4}}\Rightarrow \frac{U_{0}^{4}}{{{3}^{2}}{{.4}^{2}}}-5,76\left( \frac{U_{0}^{2}}{{{3}^{2}}}+\frac{U_{0}^{2}}{{{4}^{2}}} \right)=0\]

\[\Rightarrow {{U}_{0}}=R\sqrt{{{3}^{2}}+{{4}^{2}}}=120V\]

Hướng dẫn

Từ đồ thị ta xác định được: ${{u}_{AM}}=150\cos \left( \omega t-\frac{\pi }{3} \right)$và ${{u}_{MB}}=120\cos \left( \omega t-\pi  \right)$

$U_{AB}^{2}=U_{AM}^{2}+U_{MB}^{2}+2{{U}_{AM}}{{U}_{MB}}\cos \left( {{\varphi }_{AM}}-{{\varphi }_{MB}} \right)\to {{U}_{AB}}\approx 137,48V$

 Lúc điện áp tức thời u_MB = - 60 và đang tăng => u_AM = 150V => u_AB = u_AM + u_MB = 150 – 60 = 90V $\to \frac{{{u}_{AB}}}{{{U}_{0}}}=\frac{{{u}_{AB}}}{{{U}_{AB}}}=\frac{90}{137,48}\approx 0,655\Rightarrow $ Chọn D

 

Hướng dẫn

Khi  $f={{f}_{1}}$ thì ${{U}_{R}}={{U}_{R\max }}\Rightarrow {{f}_{1}}=\frac{1}{2\pi \sqrt{LC}}\left( 1 \right)$

Khi $f={{f}_{2}}$ thì ${{U}_{L}}={{U}_{L\max }}\Rightarrow {{f}_{2}}=\frac{1}{2\pi C\sqrt{\frac{2}{\frac{2L}{C}-{{R}^{2}}}}}\left( 2 \right)$

Khi $f={{f}_{3}}$ thì ${{U}_{C}}={{U}_{C\max }}\Rightarrow {{f}_{3}}=\frac{1}{2\pi L\sqrt{\frac{\frac{2L}{C}-{{R}^{2}}}{2}}}\left( 3 \right)$

Từ (1), (2), (3) $\Rightarrow {{f}_{2}}.{{f}_{3}}=f_{1}^{2}$

 

Hướng dẫn

Ta có: $C{{R}^{2}}<2L\leftrightarrow {{R}^{2}}<{{Z}_{L}}{{Z}_{C}}$

Từ đồ thị, ta thấy: \[{{U}_{M}}={{U}_{C\max }}={{U}_{L\max }}=\frac{2U.L}{R\sqrt{4LC-{{R}^{2}}{{C}^{2}}}}=\frac{2{{U}_{0}}}{\sqrt{\frac{4{{R}^{2}}C}{L}-{{R}^{4}}\frac{{{C}^{2}}}{{{L}^{2}}}}}\]

Xét: \[A=\frac{4{{R}^{2}}C}{L}-{{R}^{4}}\frac{{{C}^{2}}}{{{L}^{2}}}\]

Mặt khác, ta có:

${{R}^{2}}<2\frac{L}{C}\to A<2\frac{L}{C}\frac{4C}{L}-{{\left( 2\frac{L}{C} \right)}^{2}}\frac{{{C}^{2}}}{{{L}^{2}}}<2.4-4=4\to {{U}_{M}}>\frac{2U}{\sqrt{A}}=\frac{2.\frac{200}{\sqrt{2}}}{\sqrt{4}}=141,42V\Rightarrow $ Chọn B

 

Hướng dẫn

Ta có: ${{Z}_{L}}=\omega L=150\Omega ;{{Z}_{C}}=\frac{1}{\omega C}=100\Omega ;r=50\sqrt{3}\Omega $

$Z=100\Omega ;{{Z}_{d}}=\sqrt{{{r}^{2}}+Z_{L}^{2}}=100\sqrt{3}$

\[i=\frac{{{U}_{0}}}{Z}\cos \left( \omega t-\frac{\pi }{6} \right)=0,01{{U}_{0}}\cos \left( \omega t-\frac{\pi }{6} \right)\]

\[{{u}_{d}}={{I}_{0}}{{Z}_{d}}\cos \left( \omega t+\frac{\pi }{6} \right)={{U}_{0}}\sqrt{3}\cos \left( \omega t+\frac{\pi }{6} \right){{u}_{d}}={{U}_{0}}\sqrt{3}\cos \left( \omega {{t}_{1}}+\frac{\pi }{6} \right)=150V\left( 1 \right)\]

\[{{u}_{C}}={{I}_{0}}{{Z}_{C}}\cos \left( \omega t-\frac{2\pi }{3} \right)={{U}_{0}}\cos \left( \omega t-\frac{2\pi }{3} \right)\]

 

Tại thời điểm ${{t}_{2}}={{t}_{1}}+\frac{1}{75}s$, ta có:

${{u}_{C}}={{U}_{0}}\cos \left( \omega \left( {{t}_{1}}+\frac{1}{75} \right)-\frac{2\pi }{3} \right)={{U}_{0}}\cos \left( \omega {{t}_{1}}+\frac{2\pi }{3} \right)={{U}_{0}}\sin \left( \omega {{t}_{1}}+\frac{\pi }{6} \right)=150V\left( 2 \right)$

Từ (1) và (2), ta có: ${{\left( \frac{{{u}_{d}}}{\sqrt{3}} \right)}^{2}}+{{\left( {{u}_{C}} \right)}^{2}}=U_{0}^{2}\leftrightarrow \frac{{{150}^{2}}}{3}+{{150}^{2}}=U_{0}^{2}\to {{U}_{0}}=100\sqrt{3}$

Hướng dẫn

Ta có   $u=150\sqrt{2}\cos \left( 100\pi t \right)V\Rightarrow 100\pi $

Khi $C={{C}_{1}}=frac62,5\pi \mu F$ thì ${{P}_{\max }}=93,75\text{W}\,{{Z}_{{{C}_{1}}}}=\frac{1}{\omega {{C}_{1}}}=160\Omega \,{{P}_{\max }}$ khi ${{I}_{\max }}$ có xảy ra cộng hưởng $\Rightarrow {{Z}_{L}}={{Z}_{C}}=160\Omega $

$P={{I}^{2}}R=\frac{{{U}^{2}}}{{{Z}^{2}}}R=\frac{{{U}^{2}}{{R}_{m}}}{R_{m}^{2}+{{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}}$

Thay số từ đề bài P = 93,75W; U = 150; ta tính được R_m = 240Ω

$C={{C}_{2}}=\frac{1}{9\pi }\Rightarrow {{Z}_{{{C}_{2}}}}=90\Omega $ thì ${{U}_{d}}$ vuông pha với ${{U}_{RC}}$ cho ta biết cuộn dây có điện trở trong r.

$I=\frac{U}{Z}=\frac{U}{\sqrt{{{R}^{2}}+{{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}}}=\frac{150}{\sqrt{{{240}^{2}}+{{\left( 160-90 \right)}^{2}}}}=0,6A$

Vì U_Lr vuông góc với U_RC nên:

$U_{Lr}^{2}+U_{RC}^{2}={{150}^{2}}U_{L}^{2}+U_{r}^{2}+U_{R}^{2}+U_{C}^{2}={{150}^{2}}$

Mặt khác theo định luật Ôm ta có:

\[U_{Rr}^{2}+{{\left( {{U}_{L}}-{{U}_{C}} \right)}^{2}}={{U}^{2}}={{150}^{2}}{{\left( {{U}_{R}}+{{U}_{r}} \right)}^{2}}+{{\left( {{U}_{L}}-{{U}_{C}} \right)}^{2}}\]\[={{150}^{2}}U_{R}^{2}+2{{U}_{R}}{{U}_{r}}+U_{r}^{2}+U_{L}^{2}+U_{L}^{2}-2.{{U}_{L}}.{{U}_{C}}={{150}^{2}}{{U}_{R}}{{U}_{r}}-{{U}_{L}}{{U}_{C}}=0\]

\[{{u}_{d}}=I.\sqrt{{{r}^{2}}+Z_{L}^{2}}=0,6.\sqrt{{{120}^{2}}+{{160}^{2}}}=120V\]

Hướng dẫn

Do hiệu điện thế U không đổi nên: $\frac{\Delta {{P}_{1}}}{\Delta {{P}_{2}}}={{\left( \frac{{{P}_{2}}}{{{P}_{1}}} \right)}^{2}}\to \frac{{{P}_{2}}}{{{P}_{1}}}=2{{H}_{1}}=90%$

$\to {{P}_{n}}=0,9{{P}_{1}}\to {{P}_{0}}=\frac{{{P}_{n}}}{90}=0,01{{P}_{1}}\left( 1 \right)$. Gọi x là số máy nhập thêm $\Rightarrow $ công suất khi nhập mới:

$\left( 90+x \right).0,01{{P}_{1}}=0,8{{P}_{2}}\to {{P}_{2}}=\frac{\left( 90+x \right).0,01{{P}_{1}}}{0,8}\left( 2 \right)$ mà ${{P}_{2}}=2{{P}_{1}}$

$\to \frac{\left( 90+x \right).0,01{{P}_{1}}}{0,8}=2{{P}_{1}}\to \left( 90+x \right)=160\to x=70\Rightarrow $ Chọn B

Bài viết gợi ý: