Câu 1: Trên mặt nước tại hai điểm A, B cách nhau 26cm, người ta đặt hai nguồn đồng bộ, dao động điều hòa theo phương thẳng đứng tạo ra sóng kết hợp với bước sóng 1,75cm, coi biên độ sóng không đổi khi truyền sóng. Gọi M là điểm trên mặt nước sao cho MA= 24cm, và M thuộc đường tròn đường kính AB.Phải dịch B dọc theo phương AB và hướng ra xa A một khoảng nhỏ nhất bao nhiêu để M là cực đại?
A. 0,83cm. B. 9,8cm. C. 3,8cm. D. 3, 4cm.
Hướng dẫn
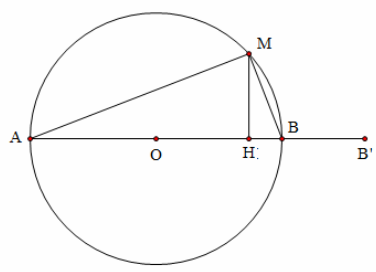
Ta có: \[MB=\sqrt{A{{B}^{2}}-M{{A}^{2}}}=10cm\Rightarrow MA-MB=1cm=8\lambda \]
\[\Rightarrow \]Lúc này M nằm trên cực đại bậc 8.
Gọi H là hình chiếu của M lên AB
.png)
Khi dịch chuyển B ra xa A để M là cực đại thì
.png)
\[\Rightarrow \]M dịch chuyên ra xa một đoạn \[d=HB'-HB=3,4cm\]
Chọn đáp án D
Câu 2: Trên mặt nước tại hai điểm A, B cách nhau 12cm, người ta đặt hai nguồn đồng bộ, dao động điều hòa theo phương thẳng đứng với tần số 20Hz. Biết tốc độtruyền sóng trên mặt nước là 32cm / s, coi biên độ sóng không đổi khi truyền sóng. Gọi M là điểm trên mặt nước sao cho MA =4,2cm,MB =9cm. Muốn M nằm trên đường cực tiểu thì phải dịch B dọc theo phương AB và hướng ra xa A một khoảng nhỏ nhất bao nhiêu?
A. 0,83cm. B. 9,8cm. C. 2,52cm. D. 9, 47cm.
Hướng dẫn
Bước sóng \[\lambda =1,6cm\Rightarrow MB-MA=3\Rightarrow \]Lúc này M nằm trên cực đại bậc 3.
Gọi H là hình chiếu của M lên AB.
Xét tam giác ABM ta có \[{{S}_{ABM}}=\sqrt{p(p-MA)(p-MB)(p-AB)}=15,12c{{m}^{2}}\]
\[\Rightarrow {{S}_{ABM}}=\frac{1}{2}MH.AB\Leftrightarrow MH=2,52cm\Rightarrow HB=\sqrt{M{{B}^{2}}-M{{H}^{2}}}=8,64cm\]
Khi dịch chuyển M ra xa A một khoảng nhỏ nhất để M là cực tiểu thì M thành cực tiểu thứ 4
Lúc này \[MB'-MA=3,5\lambda \Rightarrow MB'=9,8cm\Rightarrow HB'=\sqrt{MB{{'}^{2}}-M{{H}^{2}}}=9,47cm\]
\[\Rightarrow d=HB'-HB=0,83cm\]
Chọn đáp án A
Câu 3: Hai nguồn kết hợp \[{{S}_{1}}\] và \[{{S}_{2}}\] cách nhau một khoảng là 50mm đều dao động theo phương trình \[u=a\cos \left( 200\pi t \right)(mm)\]trên mặt nước. Biết tốc độ truyền sóng trên mặt nước 0,8 m / s và biên độ sóng không đổi khi truyền đi. Hỏi điểm gần nhất dao động cùng pha với các nguồn nằm trên đường trung trực của \[{{S}_{1}}{{S}_{2}}\] cách nguồn \[{{S}_{1}}\] bao nhiêu?
A. 32mm. B. 28mm. C. 34mm. D. 25mm.
Hướng dẫn
Gọi O là trung điểm của \[{{S}_{1}}{{S}_{2}}\Rightarrow {{S}_{1}}O=25mm\]
Bước sóng \[\lambda =vT=0,8\] cm. Gọi M là điểm dao động cùng pha với các nguồn.
M dao động cùng pha với nguồn khi \[M{{S}_{1}}=k\lambda \]
Lại có \[M{{S}_{1}}>{{S}_{1}}O\Rightarrow 8\lambda >25\Rightarrow \lambda >3,125\]
M gần nguồn nhất khi \[k=4\Rightarrow M{{S}_{1}}=3,2cm=32mm\]
Chọn đáp án A
Câu 4: Trên mặt nước nằm ngang có 2 nguồn kết hợp A, B cách nhau 10cm dao động theo phương thẳng đứng, cùng pha với biên độ 3mm, tạo ra các sóng kết hợp lan truyền với bước sóng 4cm. Số điểm dao động với biên độ 4mm trên AB là bao nhiêu?
A. 12. B. 24. C. 20. D. 10.
Hướng dẫn
Biên độ dao động của các điểm trên phương truyền sóng \[A=6\cos \left[ \frac{\pi \left( {{d}_{2}}-{{d}_{1}} \right)}{\lambda } \right]\left( mm \right)\]
Ta có \[A=4=6\cos \left[ \frac{\pi \left( {{d}_{2}}-{{d}_{1}} \right)}{\lambda } \right]\Leftrightarrow \frac{\pi \left( {{d}_{2}}-{{d}_{1}} \right)}{\lambda }=\pm \text{ar}\cos \left( \frac{4}{6} \right)+k2\pi \Rightarrow {{d}_{2}}-{{d}_{1}}=\pm 1,07+8k\]
Số điểm dao động với biên độ 3mm là \[-10<{{d}_{2}}-{{d}_{1}}<10\Leftrightarrow -40<1,07+8k<40\]
Với
.png)
Với
.png)
\[\Rightarrow \] Có tổng cộng 20 điểm dao động với biên độ 4 mm.
Chọn đáp án C
Câu 5: Hiện tường giao thoa sóng trên mặt nước với hai nguồn \[{{S}_{1}},{{S}_{2}}\] có cùng biên độ, cùng pha cách nhau 13cm. Tia \[{{S}_{1}}y\] trên mặt nước. Ban đầu \[{{S}_{1}}y\] chứa \[{{S}_{1}}{{S}_{2}}\]. Điểm C luôn trên \[{{S}_{1}}y\] và \[{{S}_{1}}C=5cm\]. Cho \[{{S}_{1}}y\] quay quanh \[{{S}_{1}}\] đến vị trí sao cho \[{{S}_{1}}C\] là trung bình nhân giữa hình chiếu của nó lên \[{{S}_{1}}{{S}_{2}}\]. Lúc này C ở trên vân cực đại giao thoa thứ 4 tính từ O (coi O là cực đại số 0). Số vân giao thoa cực tiểu quan sát được là
A. 12. B. 13. C. 14. D. 11.
Hướng dẫn
Tại vị trí đang xét của C, tam giác \[{{S}_{1}}C{{S}_{2}}\] vuông tại C \[\Rightarrow {{S}_{2}}C=12cm\]
Vì tại C là vân giao thoa cực đại thứ tư tính từ đương trung trực
Ta có \[{{S}_{2}}C-{{S}_{1}}C=(3+0,5)\lambda =7cm\Rightarrow \lambda =2cm\]
Lại có
.png)
=> Có 13 vân giao thoa cực tiểu.
Chọn đáp án B
Câu 6: Trong một thí nghiệm giao thoa sóng trên mặt nước, A và B là hai nguồn sóng nước giống nhau cách nhau 4cm, dao động theo phương thẳng đứng. Gọi C là một điểm trên mặt nước, sao cho AC vuông góc với AB. Giá trị lớn nhát của đoạn AC đểC nằm trên đường cực tiểu giao thoa là 4,2cm. Bước sóng có giá trị bằng bao nhiêu?
A.3,2cm B.2,5cm C.1,6cm D.5,0cm
Hướng dẫn
AC lớn nhất để C nằm trên đoạn giao thoa cực tiểu
\[\Rightarrow \]C nằm trên đường cực tiểu thứ 0,5 \[\Rightarrow BC-AC=0,5\lambda \]
Mặt khác \[B{{C}^{2}}-A{{C}^{2}}=A{{B}^{2}}\Rightarrow NC=5,8cm\Rightarrow \lambda =3,2cm\]
Chọn đáp án A
Câu 7: Hai nguồn sóng A và B dao động cùng pha, cùng tần số nằm trên mặt chất lỏng, giả sử biên độ sóng không đổi trong quá trình truyền sóng, khi có giao thoa quan sát thấy trên đoạn AB có 11 điểm dao động với biên độ cực đại, trên đường thẳng Ax vuông góc với AB có hai điểm M và N dao động với biên độ cực đại, với M là cực đại gần A nhất và N là cực đại xa A nhất, biết AM= 2cm và AN = 31cm. Khoảng cách giữa hai nguồn AB là
A.11,2cm B.12,8cm C.12,5cm D.10,6cm
Hướng dẫn
Trên AB có 11 điểm dao động cực đại \[\Rightarrow \] mỗi bên có 5 điểm dao động cực đại
M dao động cực đại gần A nhất \[\Rightarrow \] M nằm trên cực đại bậc 5 \[\Rightarrow MB-MA=5\lambda \]
\[M{{A}^{2}}+A{{B}^{2}}=M{{B}^{2}}\Leftrightarrow A{{B}^{2}}=25{{\lambda }^{2}}+20\lambda (1)\]
N dao động cực đại xa A nhất \[\Rightarrow \]N nằm trên cực đại bậc 1 \[\Rightarrow NB-NA=\lambda \]
\[N{{A}^{2}}+A{{B}^{2}}=N{{B}^{2}}\Leftrightarrow A{{B}^{2}}={{\lambda }^{2}}+62\lambda (2)\]
Từ (1) và (2) \[\Rightarrow 25{{\lambda }^{2}}+62\lambda ={{\lambda }^{2}}+62\lambda \Leftrightarrow \lambda =\frac{7}{4}\]
\[\Rightarrow AB=10,6cm\]
Chọn đáp án D
Câu 8: Trong thí nghiệm giao thoa sóng nước, hai nguồn \[{{S}_{1}},{{S}_{2}}\] cách nhau 16cm, dao động theo phương vuông góc với mặt nước, cùng biên độ, cùng pha, cùng tần số 80Hz. Tốc độ truyền sóng trên mặt nước là 40cm/s. Ởmặt nước, gọi d là đường trung trực của đoạn \[{{S}_{1}}{{S}_{2}}\]. Trên d, điểm M ở cách \[{{S}_{1}}\] là 10cm; điểm N dao động cùng pha với M và gần M nhất sẽ cách M một đoạn bằng bao nhiêu?
A.0,80cm B.0,88cm C.1,25cm D.2,25cm
Hướng dẫn
Bước sóng \[\lambda =0,5cm\].Gọi O là trung điểm của hai nguồn \[\Rightarrow MO=\sqrt{{{S}_{1}}{{M}^{2}}-{{S}_{1}}{{O}^{2}}}=6cm\]
Điểm M nằm trên đường trung trực trễ pha so với nguồn góc \[{{\varphi }_{M}}=\frac{2\pi {{d}_{{{S}_{1}}M}}}{\lambda }=40\pi rad\]
N gần M nhất và dao động cùng pha với M \[\Rightarrow {{\varphi }_{N}}=42\pi rad\]
Ta có \[\frac{2\pi {{d}_{{{S}_{1}}N}}}{\lambda }=42\pi \Rightarrow {{d}_{{{S}_{1}}N}}=10,5cm\Rightarrow ON=\sqrt{{{S}_{1}}{{N}^{2}}-{{S}_{1}}{{O}^{2}}}=6,8cm\Rightarrow MN=0,8cm\]
Chọn đáp án A
Câu 9: Trong thí nghiệm giao thoa với hai nguồn sóng A và B giống nhau trên mặt nước. Hai sóng truyền đi có bước sóng 2cm. Tại điểm M trên miền gặp nhau của hai sóng có hiệu đường đi bằng 3,5cm. M’ là điểm đối xứng với M qua trung điểm của đoạn AB. Trên đoạn MM’ có bao nhiêu điểm dao động với biên độ bằng \[a\sqrt{2}\] (với a là biên độ của mỗi nguồn) là
A.4 B.6 C.5 D.8
Hướng dẫn
Biên độ dao động của một điểm trên mặt nước là \[A=2a\cos \left[ \frac{\pi \left( {{d}_{2}}-{{d}_{1}} \right)}{\lambda } \right]\]
\[\Rightarrow \]\[2a\cos \left[ \frac{\pi \left( {{d}_{2}}-{{d}_{1}} \right)}{\lambda } \right]=a\sqrt{2}\Rightarrow \frac{\pi \left( {{d}_{2}}-{{d}_{1}} \right)}{\lambda }=\pm \frac{\pi }{4}\pm k2\pi \Leftrightarrow {{d}_{2}}-{{d}_{1}}=\pm 0,5+4k\]
Số điểm dao động với biên độ bằng \[a\sqrt{2}\] trên mỗi nguồn là \[-3,5<\pm 0,5+4k<3,5\]
Với \[-3,5<0,5+4k<3,5\Leftrightarrow -1\le k\le 0,75\Rightarrow k=\left[ -1;0 \right]\]
Với \[-3,5<-0,5+4k<3,5\Leftrightarrow -0,75\le k\le 1\Rightarrow k=\left[ 0;1 \right]\]
\[\Rightarrow \] Có 4 điểm dao động với biên độ \[a\sqrt{2}\] trên đoạn MM’
Chọn đáp án A
Câu 10: Trong một thí nghiệm về giao thoa sóng nước, hai nguồn kết hợp \[{{O}_{1}}\] và \[{{O}_{2}}\] cách nhau 6cm, dao động cùng pha, cùng biên độ. Chọn hệ trục tọa độ vuông góc xOy thuộc mặt nước với gốc tọa độ là vị trí đặt nguồn \[{{O}_{1}}\] , còn nguồn \[{{O}_{2}}\] nằm trên trục Oy. Hai điểm P và Q nằm trên Ox có OP =4,5cm và OQ= 8cm. Biết phần tử nước tại P không dao động còn phần tử nước tại Q dao động với biên độ cực đại. Biết giữa P và Q còn có một cực đại. Tìm bước sóng.
A.2/3cm B.2,0cm C.2,5cm D.1,0cm
Hướng dẫn
Dựa vào hình vẽ
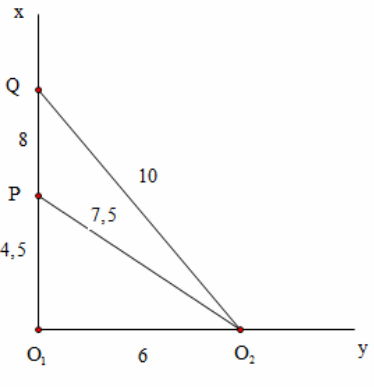
Ta có \[{{O}_{2}}P=\sqrt{{{O}_{2}}O_{1}^{2}+{{O}_{1}}{{P}^{2}}}=7,5cm\]
P không dao động \[\Rightarrow {{O}_{2}}P-{{O}_{1}}P=(k+0,5)\lambda \]
\[\Rightarrow (k+0,5)\lambda =3\Leftrightarrow \lambda k+0,5\lambda =3cm(1)\]
Lại có: \[{{O}_{2}}Q=\sqrt{{{O}_{2}}O_{1}^{2}+{{O}_{1}}{{Q}^{2}}}=10cm\]
Q dao động với biên độ cực đại và giữa P , Q còn có một cực đại \[\Rightarrow {{O}_{2}}Q-{{O}_{1}}Q=(k-1)\lambda \Leftrightarrow \lambda k-\lambda =2cm(2)\]
Từ (1) và (2) \[3-0,5\lambda -\lambda =2\Leftrightarrow \lambda =\frac{2}{3}cm\]
Chọn đáp án A







