Câu 1: Một học sinh dùng đồng hồ bấm giây để đo chu kỳ dao động điều hòa T của một vật bằng cách đo thời gian mỗi dao động. Ba lần đo cho kết quảthời gian của mỗi dao động lần lượt là 2,00 s; 2,05 s; 2,00 s. Thang chia nhỏnhất của đồng hồlà 0,01s. Kết quả của phép đo chu kỳ được biểu diễn bằng
A.\[T=2,025\pm 0,024(s)\]
B.\[T=2,030\pm 0,024(s)\]
C.\[T=2,024\pm 0,024(s)\]
D.\[T=2,022\pm 0,033(s)\]
Hướng dẫn
Ta có: \[T=\frac{{{T}_{1}}+{{T}_{2}}+{{T}_{3}}}{3}=2,022s\]
\[\vartriangle {{T}_{1}}=\left| {{T}_{1}}-T \right|=0,02\]
\[\begin{align}
& \vartriangle {{T}_{1}}=\left| {{T}_{1}}-T \right|=0,02 \\
& \vartriangle {{T}_{2}}=\left| {{T}_{2}}-T \right|=0,03 \\
& \vartriangle {{T}_{3}}=\left| {{T}_{3}}-T \right|=0,02 \\
& \vartriangle \overline{T}=\frac{\vartriangle {{T}_{1}}+\vartriangle {{T}_{2}}+\vartriangle {{T}_{3}}}{3}=\text{0,02333}...\text{ }\!\!\tilde{\ }\!\!\text{ 0,023} \\
\end{align}\]
Vì sai số có đóng góp của sai số ngẫu nhiên là \[\vartriangle \overline{T}\] cộng với sai số hệ thống (chính là sai số của dụng cụ= 0,01) khi đó sai số gặp phải là: \[\vartriangle T=\vartriangle \overline{T}+\vartriangle {{T}_{dc}}\] lúc đó kết quả đúng là T = (2,022 ±0,033) s
Chọn đáp án D
Câu 2: Để đo lực kéo về cực đại của một lò xo dao động với biên độ A ta chỉcần dùng dụng cụ đo là
A. Thước mét B. Lực kế C. Đồng hồ D. Cân.
Hướng dẫn
HD: Ta sử dụng lực kế để đo lực
Chọn đáp án B
Câu 3: Cho con lắc lò xo đặt tại nơi có gia tốc trọng trường đã biết. Bộ dụng cụ không thể dùng để đo độ cứng của lò xo là
A. thước và cân B. lực kế và thước
C. đồng hồ và cân D. lực kế và cân.
Hướng dẫn
Thước đo độ biến dạng của lò xo tại vị trí cân bằng, cân đo khối lượng của vật, sử dụng \[\vartriangle \text{l=}\frac{mg}{k}\Rightarrow k\]
Đồng hồ bấm chu kỳ của con lắc, cân để đo khối lượng của vật, sử dụng công thức: \[T=2\pi \sqrt{\frac{m}{k}}\Rightarrow k\]
Lực kế đo lực đàn hồi, thước đo vị trí, sử dụng \[F=kx\Rightarrow k\]
Chọn đáp án B
Câu 4: Để đo bước sóng của bức xạ đơn sắc trong thí nghiệm giao thoa khe Y âng, ta chỉ cần dùng dụng cụ đo là
A. thước B. cân C. nhiệt kế D. đồng hồ.
Hướng dẫn
\[\lambda =\frac{ai}{D}\] dùng thước đo a, i, D ta có thể xác định được λ
Chọn đáp án A
Câu 5: Để đo công suất tiêu thụ trung bình trên đoạn mạch chỉ có điện trở thuần, ta cần dùng dụng cụ đo là
A. chỉ Ampe kế
B. chỉ Vôn kế
C. Ampe kế và Vôn kế
D. Áp kế.
Hướng dẫn
Công suất tiêu thụ trung bình trên đoạn mạch chỉ có R:
P= UI : dùng Ampe kế đo I, vôn kế đo U\[\Rightarrow \]P
Chọn đáp án A
Câu 6: Để đo gia tốc trọng trường dựa vào dao động của con lắc đơn, ta cần dùng dụng cụ đo là
A. chỉ đồng hồ B. đồng hồ và thước C. cân và thước D. chỉ thước.
Hướng dẫn
Dùng đồng hồ bấm T, thước đo ℓ \[\Rightarrow g=\frac{4{{\pi }^{2}}l}{T}\]
Chọn đáp án B
Câu 7: Một học sinh làm thí nghiệm đo gia tốc trọng trường dựa vào dao động của con lắc đơn. Dùng đồng hồ bấm giây đo thời gian 10 đao động toàn phần và tính được kết quả \[t=20,012\pm 0,269(s)\] . Dùng thước đo chiều dài dây treo và tính được kết quả \[L=1\pm 0,001\left( m \right)\]. Lấy \[{{\pi }^{2}}\] và bỏ qua sai số của số pi (π). Kết quả gia tốc trọng trường tại nơi đặt con lắc đơn là
A.\[9,899(m/{{s}^{2}})\pm 1,438%\]
B.\[9,998(m/{{s}^{2}})\pm 1,438%\]
C.\[9,899(m/{{s}^{2}})\pm 2,776%\]
D.\[9,998(m/{{s}^{2}})\pm 2,776%\]
Hướng dẫn
\[T=\frac{t}{10}\Rightarrow \vartriangle T=\frac{\vartriangle t}{10}\Rightarrow \frac{\vartriangle T}{T}=\frac{\vartriangle t}{t}\]
Ta có: \[T=2\pi \sqrt{\frac{l}{g}}\Rightarrow g=\frac{4{{\pi }^{2}}l}{{{T}^{2}}}\Rightarrow \overline{g}=\frac{4{{\pi }^{2}}\overline{L}}{\overline{{{T}^{2}}}}=9,899\]
\[\frac{\vartriangle g}{\overline{g}}=\frac{\vartriangle L}{\overline{L}}+2\frac{\vartriangle T}{\overline{T}}=\frac{0,001}{1}+2.\frac{2,069}{20,012}=2,776%\Rightarrow g=9,899(m/{{s}^{2}})\pm 2,776%\]
Chọn đáp án C
Câu 8: Một học sinh dùng cân và đồng hồ bấm giây để đo độ cứng của lò xo. Dùng cân để cân vật nặng và cho kết quả khối lượng \[m=100g\pm 2%\] . Gắn vật vào lò xo và kích thích cho con lắc dao động rồi dùng đồng hồ bấm giây đo thời gian t của một dao động, kết quả \[t=2s\pm 1%\] Bỏ qua sai số của số pi (π). Sai số tương đối của phép đo độ cứng lò xo là
A. 4% B. 2% C. 3% D. 1%.
Hướng dẫn
Ta có: \[T=2\pi \sqrt{\frac{m}{k}}\Rightarrow k=\frac{4{{\pi }^{2}}m}{{{T}^{2}}}\]
Sai số tương đối của phép đo độ cứng lò xo là \[\frac{\vartriangle k}{\overline{k}}=\frac{\vartriangle m}{\overline{m}}+2\frac{\vartriangle T}{\overline{T}}=4%\]
Chọn đáp án A
Câu 9: Để đo tốc độ truyền sóng v trên một sợi dây đàn hồi AB, người ta nối đầu A vào một nguồn dao động có tần số \[f=100Hz\pm 0,02%\] .Đầu B được gắn cố định. Người ta đo khoảng cách giữa hai điểm trên dây gần nhất không dao động với kết quả \[d=0,02m\pm 0,82%\]. Tốc độ truyền sóng trên sợi dây AB là
A.\[v=2(m/s)\pm 0,84%\]
B.\[v=4(m/s)\pm 0,016%\]
C.\[v=4(m/s)\pm 0,84%\]
D.\[v=2(m/s)\pm 0,016%\]
Hướng dẫn
Khoảng cách giữa hai điểm gần nhất không dao động bằng λ/2 \[\Rightarrow \lambda =0,04\left( m \right)\pm 0,82%\]
Ta có:
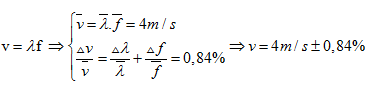
Chọn đáp án C
Câu 10: Để đo tốc độ truyền sóng v trên một sợi dây đàn hồi AB, người ta nối đầu A vào một nguồn dao động có tần số \[f=100Hz\pm 0,02%\] .Đầu B được gắn cố định. Người ta đo khoảng cách giữa hai điểm trên dây gần nhất không dao động với kết quả \[d=0,02m\pm 0,82%\]. Tốc độ truyền sóng trên sợi dây AB là
A. \[v=2m/s\pm 0,02(m/s)\]
B.\[v=4m/s\pm 0,01(m/s)\]
C.\[v=4m/s\pm 0,03(m/s)\]
D. \[v=2m/s\pm 0,04(m/s)\]
Hướng dẫn
Khoảng cách giữa hai điểm gần nhất không dao động bằng λ/2 \[\Rightarrow \lambda =0,04\left( m \right)\pm 0,82%\]
Ta có:
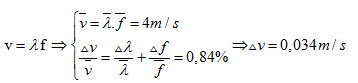
Lấy sau dấu thập phân 2 chữ số \[\Rightarrow \] \[v=4m/s\pm 0,03(m/s)\]
Chọn đáp án C
Câu 11: : Một học sinh làm thí nghiệm đo gia tốc trọng trường dựa vào dao động của con lắc đơn. Dùng đồng hồ bấm giây đo thời gian 10 đao động toàn phần và tính được kết quả \[t=20,012\pm 0,269(s)\] . Dùng thước đo chiều dài dây treo và tính được kết quả \[L=1\pm 0,001\left( m \right)\]. Lấy \[{{\pi }^{2}}\] và bỏ qua sai số của số pi (π). Kết quả gia tốc trọng trường tại nơi đặt con lắc đơn là
A. \[g=9,899\pm 0,142(m/{{s}^{2}})\]
B.\[g=9,988\pm 0,144(m/{{s}^{2}})\]
C.\[g=9,899\pm 0,275(m/{{s}^{2}})\]
D.\[g=9,988\pm 0,277(m/{{s}^{2}})\]
Hướng dẫn
\[T=\frac{t}{10}\Rightarrow \vartriangle T=\frac{\vartriangle t}{10}\Rightarrow \frac{\vartriangle T}{T}=\frac{\vartriangle t}{t}\]
Ta có: \[T=2\pi \sqrt{\frac{l}{g}}\Rightarrow g=\frac{4{{\pi }^{2}}l}{{{T}^{2}}}\Rightarrow \overline{g}=\frac{4{{\pi }^{2}}\overline{L}}{\overline{{{T}^{2}}}}=9,899\]
\[\frac{\vartriangle g}{\overline{g}}=\frac{\vartriangle L}{\overline{L}}+2\frac{\vartriangle T}{\overline{T}}=\frac{0,001}{1}+2.\frac{2,069}{20,012}=2,776%\Rightarrow \vartriangle g=2,776%.9,899(m/{{s}^{2}})=0,275\]
- \[g=9,899\pm 0,275(m/{{s}^{2}})\]
Chọn đáp án C
Câu 12: Một học sinh làm thí nghiệm đo bước sóng của nguồn sáng bằng thí nghiệm khe Young. Giá trị trung bình và sai số tuyệt đối của phép đo khoảng cách hai khe sáng là \[\overline{a}\] và \[\vartriangle a\].Giá trị trung bình và sai số tuyệt đối của phép đo khoảng cách từ mặt phẳng chứa hai khe đến màn đo được là \[\overline{D}\] và \[\vartriangle D\]. Giá trị trung bình và sai số tuyệt đối của phép đo khoảng vân là \[\overline{i}\] và \[\vartriangle i\].Kết quả sai số tương đối của phép đo bước sóng được tính.
A.\[\varepsilon (%)=\left( \frac{\vartriangle a}{\overline{a}}+\frac{\vartriangle i}{\overline{i}}-\frac{\vartriangle D}{\overline{D}} \right).100%\]
B.\[\varepsilon (%)=\left( \vartriangle a+\vartriangle i+\vartriangle D \right).100%\]
D.\[\varepsilon (%)=\left( \frac{\vartriangle a}{\overline{a}}+\frac{\vartriangle i}{\overline{i}}+\frac{\vartriangle D}{\overline{D}} \right).100%\]
D.\[\varepsilon (%)=\left( \vartriangle a+\vartriangle i-\vartriangle D \right).100%\]
Hướng dẫn
Ta có: \[\lambda =\frac{ai}{D}\Rightarrow \] sai số tương đối của phép đo bước sóng: \[\varepsilon (%)=\left( \frac{\vartriangle a}{\overline{a}}+\frac{\vartriangle i}{\overline{i}}+\frac{\vartriangle D}{\overline{D}} \right).100%\]
Chọn đáp án C
Câu 13: Dùng một thước chia độ đến milimet đo khoảng cách d giữa hai điểm A và B, cả 5 lần đo đều cho cùng giá trị là 1,345 m. Lấy sai số dụng cụ là một độ chia nhỏ nhất. Kết quả đo được viết là
A.\[d=\left( 1345\pm 2 \right)mm\]
B.\[d=\left( 1345\pm 0,001 \right)m\]
C.\[d=\left( 1345\pm 3 \right)mm\]
D.\[d=\left( 1345\pm 0,0005 \right)m\]
Hướng dẫn
Thước đo sau dấu phẩy 3 chữ số \[\Rightarrow \] sai số dụng cụ là một độ chia nhỏ nhất =0,001 m
Chỉ có sai số do dụng cụ nên kết quả đo được viết là: \[d=\left( 1345\pm 0,001 \right)m\]
Chọn đáp án B
Câu 14: Một học sinh làm thí nghiệm đo bước sóng của nguồn sáng bằng thí nghiệm khe Young. Khoảng cách hai khe sáng là \[1,00+0,05mm\]. Khoảng cách từ mặt phẳng chứa hai khe đến màn đo được là \[2000\pm 1,54\left( mm \right)\] ; khoảng cách 10 vân sáng liên tiếp đo được là \[10,80\pm 0,14\left( mm \right)\] . Kết quả bước sóng bằng
A. \[0,6\mu m\pm 6,37%\]
B.\[0,54\mu m\pm 6,22%\]
C.\[0,54\mu m\pm 6,37%\]
D.\[0,60\mu m\pm 6,22%\]
Hướng dẫn
Khoảng cách 10 vân sáng liên tiếp là 9 khoảng vân: \[i=1,2mm\] ;\[\vartriangle i=\frac{0,14}{9}mm\]
Bước sóng : \[\lambda =\frac{ai}{D}\Rightarrow \overline{\lambda }=\frac{\overline{a}\overline{i}}{\overline{D}}=0,6\mu m\]
Sai số tương đối của phép đo: \[\frac{\vartriangle \lambda }{\lambda }=\left( \frac{\vartriangle a}{\overline{a}}+\frac{\vartriangle i}{\overline{i}}+\frac{\vartriangle D}{\overline{D}} \right)=6,37%\]
Lấy sai số đến 2 chữ số \[\Rightarrow \] \[0,6\mu m\pm 6,37%\]
Chọn đáp án A
Câu 15: Một học sinh làm thí nghiệm đo bước sóng của nguồn sáng bằng thí nghiệm khe Young. Khoảng cách hai khe sáng là \[1,00+0,05mm\]. Khoảng cách từ mặt phẳng chứa hai khe đến màn đo được là \[2000\pm 1,54\left( mm \right)\] ; khoảng cách 10 vân sáng liên tiếp đo được là \[10,80\pm 0,14\left( mm \right)\] . Kết quả bước sóng bằng
A.\[0,600\mu m\pm 0,038\mu m\]
B.\[0,540\mu m\pm 0,034\mu m\]
C.\[0,540\mu m\pm 0,038\mu m\]
D.\[0,600\mu m\pm 0,034\mu m\]
Hướng dẫn
Khoảng cách 10 vân sáng liên tiếp là 9 khoảng vân: \[i=1,2mm\] ;\[\vartriangle i=\frac{0,14}{9}mm\]
Bước sóng : \[\lambda =\frac{ai}{D}\Rightarrow \overline{\lambda }=\frac{\overline{a}\overline{i}}{\overline{D}}=0,6\mu m\]
Sai số tương đối của phép đo: \[\frac{\vartriangle \lambda }{\lambda }=\left( \frac{\vartriangle a}{\overline{a}}+\frac{\vartriangle i}{\overline{i}}+\frac{\vartriangle D}{\overline{D}} \right)=6,37%\]
\[\Rightarrow \vartriangle \lambda =6,37%.0,60=0,0382\mu m\]
Lấy sai số đến 3 chữ số \[\Rightarrow \] \[0,600\mu m\pm 0,038\mu m\]
Chọn đáp án A







