Câu 1: M, N, P là 3 điểm liên tiếp nhau trên một sợi dây mang sóng dừng có cùng biên độ \[\sqrt{3}cm\] , dao động tại N cùng pha với dao động tại P. Biết MN= 2NP= 40cm và tần số góc của sóng là 20 rad/s. Tính tốc độ dao động tại điểm bụng khi sợi dây có dạng một đoạn thẳng.
A.40m/s B.\[40\sqrt{3}cm/s\] C.40cm/s D.\[40\sqrt{3}m/s\]
Hướng dẫn
Dao động tại N cùng pha dao động tại P \[\Rightarrow \] N và P cùng nằm trên một bó sóng
Ta có \[\lambda =2(MN+NP)=120cm\]. N cách bụng sóng một khoảng \[d=\frac{NP}{2}=20cm\]
Ta có: \[{{A}_{N}}={{A}_{B}}\cos \left( \frac{2\pi .20}{120} \right)=\frac{{{A}_{B}}}{2}\Leftrightarrow {{A}_{B}}=2\sqrt{3}cm\Rightarrow {{v}_{\max }}=\omega A=40\sqrt{3}cm/s\]
Chọn đáp án B
Câu 2: Trong thí nghiệm về sự phản xạ sóng trên vật cản cố định. Sợi dây mềm AB có đầu B cố định, đầu A dao động điều hòa. ba điểm M, N, P không phải là nút sóng, nằm trên sợi dây cách nhau \[MN=\frac{\lambda }{2}\];\[MP=\frac{\lambda }{2}\]. Khi điểm M đi qua vịtrí cân bằng (VTCB) thì
A. điểm N có li độ cực đại, điểm P đi qua VTCB.
B.N đi qua VTCB, điểm P có li độ cực đại.
C. điểm N và điểm P đi qua VTCB.
D. điểm N có li độ cực tiểu, điểm P có li độ cực đại.
Hướng dẫn
Ta có: \[MP=\frac{\lambda }{2}\]và \[MN=\frac{\lambda }{2}\]\[\Rightarrow \] Các điểm này có thể dao động ngược pha, hoặc cùng pha
\[\Rightarrow \] Điểm N và điểm P đi qua VTCB.
Chọn đáp án C
Câu 3: Trên một sợi dây hai đàn hồi cố định có sóng dừng với bước sóng là λ. Trên đây, B là một điểm bụng, C là điểm cách B là λ /12. Khoảng thời gian ngắn nhất giữa hai lần kế tiếp mà li độ của phần tử sóng tại B bằng biên độ tại C là 0,15s. Tốc độ truyền sóng trên dây là 40cm / s. Tại điểm D trên dây cách B là 24cm có biên độlà 4,5mm. Tốc độ dao động cực đại của phần tử sóng tại B bằng
A.\[20\pi \left( mm/s \right)\]
B.\[25\pi \left( mm/s \right)\]
C.\[25\sqrt{3}\pi \left( mm/s \right)\]
D.\[20\sqrt{3}\pi \left( mm/s \right)\]
Hướng dẫn
Biên độ dao động tại C là \[{{A}_{C}}={{A}_{B}}\frac{\sqrt{3}}{2}\]
\[\Rightarrow \]Khoảng thời gian ngắn nhất giữa hai lần kế tiếp mà li độ của phần tử sóng tại B bằng biên độ tại C là \[t=\frac{T}{12}+\frac{T}{12}=\frac{T}{6}=0,15\Leftrightarrow T=0,9s\]
Bước sóng \[\lambda =vT=36cm\]
Biên độ dao động tại D là \[{{A}_{D}}={{A}_{B}}\cos \left( \frac{2\pi .24}{36} \right)=\frac{{{A}_{B}}}{2}\Leftrightarrow {{A}_{B}}=9cm\]
Tốc độ dao động cực đại tại B là \[{{v}_{\max }}={{A}_{B}}\frac{2\pi }{T}=20\pi mm/s\]
Chọn đáp án A
Câu 4: Trên một sợi dây AB dài 1,2m đang có sóng dừng với 3 bụng sóng, biên độ bụng sóng là \[4\sqrt{2}cm\]. Tốc độ truyền sóng trên dây là 80cm / s. Biết hai đầu A, B là các nút sóng. Ở thời điểm phần từ tử tại điểm M trên dây cách A là 30cm có li độ 2cm thì phần tử tại điểm N trên dây cách B là 50cm có tốc độ là
A.\[4\pi \sqrt{3}cm/s\]
B.\[8\pi \sqrt{3}cm/s\]
C.\[8\pi cm/s\]
D.\[4\pi cm/s\]
Hướng dẫn
Điều kiện sóng dừng với 2 đầu cố định: \[l=\frac{k\lambda }{2}\Rightarrow \lambda =0,8m=80cm\]
\[\Rightarrow f=\frac{v}{\lambda }=1Hz\Rightarrow \omega =2\pi rad/s\]
Ta có: \[A={{A}_{b}}\sin \frac{2\pi d}{\lambda }\]
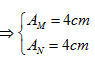
Độ lệch pha giữa M và N là
\[\begin{align}
& \vartriangle \varphi =\frac{2\pi \left( AN-AM \right)}{\lambda }=\pi \\
& \Rightarrow \frac{{{x}_{M}}}{{{A}_{M}}}=-\frac{{{x}_{N}}}{{{A}_{N}}}\Rightarrow {{x}_{N}}=-2cm\Rightarrow \left| {{v}_{N}} \right|=\omega \sqrt{A_{N}^{2}-x_{N}^{2}}=4\pi \sqrt{3}cm/s \\
\end{align}\]
Chọn đáp án A
Câu 5: Thí nghiệm sóng dừng trên một sợi dây có hai đầu cố định và chiều dài 36cm, người ta thấy có 6 điểm trên dây dao động với biên độ cực đại. Khoảng thời gian ngắn nhất giữa hai lần dây duỗi thẳng là 0,25s. Khoảng cách từ bụng sóng đến điểm gần nó nhất có biên độ bằng nửa biên độ của bụng sóng là
A. 4cm. B. 2cm. C. 3cm. D. 1cm.
Hướng dẫn
Điều kiện sợi dây 2 đầu cố định có sóng dừng: \[l=6\frac{\lambda }{2}=36\Rightarrow \lambda =12cm\]
Công thức tính biên độ: \[A={{A}_{b}}\sin \frac{2\pi d}{\lambda }\Leftrightarrow \frac{{{A}_{b}}}{2}={{A}_{b}}\sin \frac{2\pi d}{\lambda }\Rightarrow d=\frac{\lambda }{12}=1cm\]
Chọn đáp án D
Câu 6: Trên một sợi dây căng ngang dài 1,92m đang có sóng dừng với 5điểm luôn đứng yên (kể cả hai đầu dây). Vận tốc truyền sóng trên dây là 9,6m / s, biên độ dao động của một bụng sóng là 4cm. Biết rằng các điểm liên tiếp trên dây dao động cùng pha, cùng biên độ thì có hiệu khoảng cách giữa chúng bằng
0,32m; tốc độ dao động cực đại của các điểm này là
A. 60πcm / s. B. 40πcm / s. C. 80πcm / s. D. 20πcm /s
Hướng dẫn
Điều kiện sợi dây 2 đầu cố định có sóng dừng: \[l=\frac{k\lambda }{2}\Rightarrow \lambda =96cm\]
\[\Rightarrow \omega =2\pi f=20\pi rad/s\]
Hai điểm cùng biên độ dao động cùng pha, cách nhau 0,32 m < 1λ \[\Rightarrow \] 2 điểm này thuộc cùng bó sóng
\[\Rightarrow \]Khoảng cách từ điểm này đến nút sóng gần nhất \[=\frac{\frac{\lambda }{2}-32}{2}=8cm\Rightarrow A=4\sin \left( \frac{2\pi .8}{96} \right)=2cm\]
\[\Rightarrow {{v}_{\max }}=\omega A=40\pi cm/s\]
Chọn đáp án B
Câu 7: Một sợi dây căng ngang với hai đầu cố định, đang có sóng dừng. Biết khoảng cách xa nhất giữa hai phần tử dây dao động với cùng biên độ 5 mm là 80 cm, còn khoảng cách xa nhất giữa hai phần tử dây dao động cùng pha với cùng biên độ 5 mm là 65cm. Tỉ số giữa tốc độ cực đại của một phần tử dây tại bụng sóng và tốc độ truyền sóng trên dây là
A. 0,12. B. 0,41. C. 0,21. D. 0,14
Hướng dẫn
Khoảng cách xa nhất giữa hai phần tử dây dao động với cùng biên độ 5 mm là 80 cm, còn khoảng cách xa nhất giữa hai phần tử dây dao động cùng pha với cùng biên độ 5 mm là 65 cm
\[\Rightarrow \frac{\lambda }{2}=15cm\Rightarrow \lambda =30cm\]
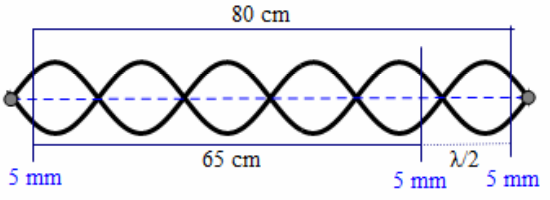
Thấy 80 cm < 3λ \[\Rightarrow \] trên sợi dây có 6 bó sóng\[\Rightarrow \] \[l=6\frac{\lambda }{2}=90cm\]
\[\Rightarrow \]Khoảng cách từ nút đến điểm có biên độ 5mm gần nhất = (90 – 80)/2 = 5 cm
Công thức biên độ:\[5={{A}_{B}}\sin \frac{2\pi .5}{30}\Rightarrow {{A}_{B}}=\frac{10}{\sqrt{3}}mm\Rightarrow \frac{{{v}_{\max }}}{v}=\frac{2\pi A}{\lambda }=0,12\]
Chọn đáp án A
Câu 8: : Sóng dừng trên dây có tần số f =20 Hz truyền đi với tốc độ 1,6 m s. Gọi N là vị trí của một nút sóng; C và D là hai vị trí cân bằng của hai phần tử trên dây cách N lần lượt là 9cm và 32/3 cm và ở hai bên của N. Tại thời điểm \[{{t}_{1}}\] li độ của phần tử tại điểm D là \[-\sqrt{3}cm\]. Li độ của phần tử tại điểm C vào thời điểm \[{{t}_{2}}={{t}_{1}}+\frac{9}{40}s\]bằng
A.\[-\sqrt{2}cm\] B.\[\sqrt{3}cm\] C.\[-\sqrt{3}cm\] D.\[\sqrt{2}cm\]
Hướng dẫn
\[\lambda =\frac{v}{f}=8cm;T=0,05s\]
Ta có: \[CN=9cm=\lambda +\frac{\lambda }{8};DN=\frac{32}{3}cm=\lambda +\frac{\lambda }{3}\]
Biên độ dao động của C và D là
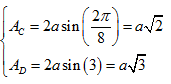
C và D cách nhau 4 bó sóng nên dao động ngược pha.
Ta có \[\frac{{{x}_{{{D}_{1}}}}}{{{A}_{D}}}=-\frac{{{x}_{{{C}_{1}}}}}{{{A}_{C}}}\Rightarrow {{x}_{{{C}_{1}}}}=\sqrt{2}cm\]
Ta có: \[\frac{9}{40}s=4T+\frac{T}{2}\Rightarrow \]Tại thời điểm \[{{t}_{2}}\]điểm C có li độ \[=-\sqrt{2}cm\]
Chọn đáp án A
Câu 9: Trên một sợi dây đàn hồi đó có sóng dừng ổn định với khoảng cách giữa hai nút sóng liên tiếp là 6cm. Trên dây có những phần tử dao động với tần số 5Hz và biên độ lớn nhất là 3cm. Gọi N là vị trí của một nút sóng, C và D là hai phần tử trên dây ở hai bên của N và có vị trí cân bằng cách N lần lượt là 10,5cm và 7cm. Tại thời điểm \[{{t}_{1}}\]phần tử C có li độ 1,5cm và đang hướng về vị trí cân bằng. Vào thời điểm \[{{t}_{2}}={{t}_{1}}+\frac{79}{40}(s)\]thì phần tử D có li độ là
A.-0,75cm. B.1,5cm. C.−1,5cm. D.0,75cm.
Hướng dẫn
\[\frac{\lambda }{2}=6\Rightarrow \lambda =12cm,T=0,2s\]
Biên độ dao động của C và D là
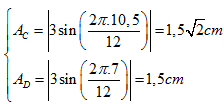
C và D nằm ở 2 bó sóng liên tiếp nên dao động ngược pha:
\[\frac{{{x}_{{{D}_{1}}}}}{{{A}_{D}}}=-\frac{{{x}_{{{C}_{1}}}}}{{{A}_{C}}}\Rightarrow {{x}_{{{C}_{1}}}}=-0,75\sqrt{2}cm\]; C đang hướng về vtcb, D ngược pha nên D cũng đang hướng về vtcb.
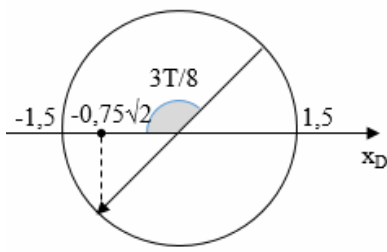
Tách \[\frac{79}{40}s=9T+\frac{T}{2}+\frac{3T}{8}\Rightarrow \]Tại thời điểm \[{{t}_{2}}\], điểm D có li độ = -1,5 cm.
Chọn đáp án C
Câu 10: Trong môi trường đẳng hướng và không hấp thụ âm, có ba điểm theo thứ tự A, B, C thẳng hàng. Một nguồn âm điểm phát âm với công suất là P và đặt tại O thì mức cường độ âm tại A và C là 30dB. Bỏ nguồn âm tại O đặt tại B một nguồn âm điểm phát âm với công suất 10P/3 thì thấy mức cường độ âm tại O và C bằng nhau và bằng 40dB, khi đó mức cường độ âm tại A gần với giá trị nào nhất sau đây?
A. 29dB. B. 34dB. C. 38dB. D. 27dB.
Hướng dẫn
Khi đặt nguồn âm tại O thì \[{{L}_{A}}={{L}_{C}}=OA=OC\Rightarrow \vartriangle OAC\] cân tại O.
Suy ra \[\frac{P}{4\pi I_{o}^{2}O{{A}^{2}}}=\frac{P}{4\pi I_{o}^{2}O{{C}^{2}}}={{10}^{{{L}_{A}}}}={{10}^{{{L}_{C}}}}={{10}^{3}}(1)\]
Khi đặt nguồn âm tại B thì \[{{L}_{o}}={{L}_{C}}\Rightarrow BC=BO\Rightarrow \vartriangle BOC\]cân tại B
\[\Rightarrow \frac{10P}{3.4\pi B{{O}^{2}}{{I}_{o}}}=\frac{10P}{3.4\pi B{{C}^{2}}{{I}_{o}}}={{10}^{{{L}_{o}}}}={{10}^{{{L}_{C}}}}={{10}^{4}}(2)\]
Từ (1)và (2), suy ra \[O{{A}^{2}}=3O{{B}^{2}}\]
Chuẩn hóa OB = 1 = BC \[\Rightarrow OA=\sqrt{3}=OC\]
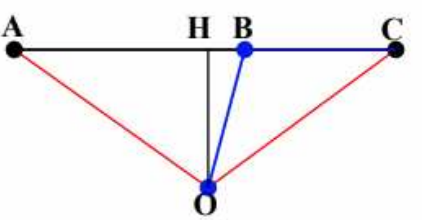
Ta có ΔOAC đồng dạng ΔBOC:
\[\Rightarrow \frac{OA}{AC}=\frac{BO}{OC}\Rightarrow AC=3\Rightarrow BA=2\]
Mức cường độ âm tại A lúc này là \[{{L}_{A}}={{L}_{B}}+\log {{\left( \frac{BC}{BA} \right)}^{2}}=3,4B=34dB\]
Chọn đáp án B
Câu 11 : Tại một điểm A nằm cách xa nguồn âm O (coi như nguồn điểm) một khoảng 1m, mức cường độ âm là 90dB. Cho biết cường độ âm chuẩn \[{{10}^{-12}}(\text{W/}{{\text{m}}^{2}})\]. Giả sử nguồn âm và môi trường đều đẳng hướng. Tính công suất phát âm của nguồn O.
A. 1 mW. B. 28,3 mW. C. 12,6 mW. D. 12,6 W
Hướng dẫn
\[{{L}_{A}}=\log \frac{{{I}_{A}}}{{{I}_{o}}}\Rightarrow {{I}_{A}}={{I}_{o}}{{.10}^{9}}={{10}^{-3}}(\text{W/}{{\text{m}}^{2}})\]
Lại có: \[I=\frac{P}{4\pi O{{A}^{2}}}\Rightarrow P=12,6mW\]
Chọn đáp án C
Câu 12: Nguồn điểm O phát sóng âm đẳng hướng ra không gian. Ba điểm O,A,B nằm trên một phương truyền sóng ( A, B cùng phía so với O, AB= 70 m). Điểm M là một điểm thuộc AB cách O một khoảng 60 m có cường độ âm \[1,5(\text{W/}{{\text{m}}^{2}})\]. Năng lượng của sóng âm giới hạn bởi 2 mặt cầu tâm O đi qua A và B , biết vận tốc truyền âm trong không khí là 340 m/s và môi trường không hấp thụ âm.
A. 5256 J . B. 13971 J . C. 16299 J . D. 10866 J .
Hướng dẫn
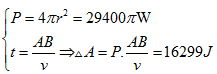
Chọn đáp án C







