Giao thoa sóng cơ

Giao thoa của hai sóng phát ra từ hai nguồn sóng kết hợp S₁, S₂ cách nhau một khoảng l:         

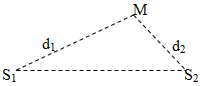
Xét 2 nguồn kết hợp u₁=A₁cos($\omega t+{{\varphi }_{1}}$), u₂=A₂cos($\omega t+{{\varphi }_{2}}$),

Xét điểm M trong vùng giao thoa có khoảng cách tới các nguồn là d_1, d₂:

Phương trình sóng do u_{1, u2} truyền tới M: u_1M = A₁cos($\omega t+{{\varphi }_{1}}-2\pi \frac{{{d}_{1}}}{\lambda }$)

u_2M = A₂cos($\omega t+{{\varphi }_{2}}-2\pi \frac{{{d}_{2}}}{\lambda }$)

Phương trình sóng tổng hợp tại M: u_M= u_1M + u_2M       

1.Độ lệch pha của hai sóng từ hai nguồn đến M là:

                                              

             Với :\[\Delta {{\varphi }_{{}}}={{\varphi }_{2}}-{{\varphi }_{1}}\]

2. Hiệu đường đi của sóng từ hai nguồn đến M là:

                                            

-Chú ý:  + \[\Delta {{\varphi }_{{}}}={{\varphi }_{2}}-{{\varphi }_{1}}\]   là độ lệch pha của hai sóng thành phần của nguồn 2 so với nguồn 1

              + \[\Delta {{\varphi }_{M}}={{\varphi }_{2M}}-{{\varphi }_{1M}}\]là độ lệch pha của hai sóng thành phần tại M của nguồn 2 so với nguồn 1 do sóng từ nguồn 2 và nguồn 1 truyền đến

.3.Dùng phương pháp giản đồ Fresnel  biểu diễn các véc tơ quay A_1, A_2, và A Ta có:

Biên độ dao động tổng hợp:     

A²=A₁²+A₂²+2A₁A₂cos[${{\varphi }_{1}}-2\pi \frac{{{d}_{1}}}{\lambda }$-(${{\varphi }_{2}}-2\pi \frac{{{d}_{2}}}{\lambda }$)]=A₁²+A₂²+2A₁A₂cos(${{\varphi }_{1}}-{{\varphi }_{2}}+2\pi \frac{{{d}_{2-}}{{d}_{1}}}{\lambda }$)

a.Biên độ dao động tổng hợp cực đại : A= A₁+A₂   khi:  cos(${{\varphi }_{1}}-{{\varphi }_{2}}+2\pi \frac{{{d}_{2-}}{{d}_{1}}}{\lambda }$) =1

                         

b.Biên độ dao động tổng hợp cực tiểu:  A=$\left| {{\mathrm{A}}_{\mathrm{1}}}\mathrm{-}{{\mathrm{A}}_{\mathrm{2}}} \right|$ khi: cos(${{\varphi }_{1}}-{{\varphi }_{2}}+2\pi \frac{{{d}_{2-}}{{d}_{1}}}{\lambda }$) = -1

                      

4.Phương trình sóng tại 2 nguồn cùng biên độ A:(Điểm M cách hai nguồn lần lượt d₁, d₂)

 ${{u}_{1}}=\text{Acos}(2\pi ft+{{\varphi }_{1}})$ và ${{u}_{2}}=\text{Acos}(2\pi ft+{{\varphi }_{2}})$

+Phương trình sóng tại M do hai sóng từ hai nguồn truyền tới:

  ${{u}_{1M}}=\text{Acos}(2\pi ft-2\pi \frac{{{d}_{1}}}{\lambda }+{{\varphi }_{1}})$ và ${{u}_{2M}}=\text{Acos}(2\pi ft-2\pi \frac{{{d}_{2}}}{\lambda }+{{\varphi }_{2}})$

+Phương trình giao thoa sóng tại M: u_M = u_1M + u_2M

${{u}_{M}}=2Ac\text{os}\left[ \pi \frac{{{d}_{1}}-{{d}_{2}}}{\lambda }+\frac{\Delta \varphi }{2} \right]c\text{os}\left[ 2\pi ft-\pi \frac{{{d}_{1}}+{{d}_{2}}}{\lambda }+\frac{{{\varphi }_{1}}+{{\varphi }_{2}}}{2} \right]$

+Biên độ dao động tại M:

                                                     

                             với $\Delta \varphi ={{\varphi }_{2}}-{{\varphi }_{1}}$

II.Tìm số điểm dao động cực đại, số điểm dao động cực tiểu giữa hai nguồn:

                             

Ta xét các trường hợp sau đây:

a. Hai nguồn dao động cùng pha: Dj = =2kp

                               

b. Hai nguồn dao động ngược pha: Dj ==(2k+1)p

                              

c. Hai nguồn dao động vuông pha: Dj =(2k+1)p/2 ( Số Cực đại= Số Cực tiểu)

                                  

     Nhận xét: số điểm cực đại và cực tiểu trên đoạn AB là bằng nhau nên có thể dùng 1 công thức là đủ

=> Số giá trị nguyên của k thoả mãn các biểu thức trên là số đường cần tìm.

III.Tìm số điểm dao động cực đại, dao động cực tiểu giữa hai điểm M N:     

1. Dùng các công thức tổng quát

a. Độ lệch pha của hai sóng từ hai nguồn đến M là                                                                   

                                                                     

                         với \[\Delta {{\varphi }_{{}}}={{\varphi }_{2}}-{{\varphi }_{1}}\]

b. Hiệu đường đi của sóng từ hai nguồn đến M là:

                                             

-Chú ý:  + \[\Delta {{\varphi }_{{}}}={{\varphi }_{2}}-{{\varphi }_{1}}\]   là độ lệch pha của hai sóng thành phần của nguồn 2 so với nguồn 1

               + \[\Delta {{\varphi }_{M}}={{\varphi }_{2M}}-{{\varphi }_{1M}}\]là độ lệch pha của hai sóng thành phần tại M của nguồn 2 so với nguồn 1 do sóng từ nguồn 2 và nguồn 1 truyền đến

c. Số điểm (đường) dao động cực đại, cực tiểu giữa hai điểm M, N thỏa mãn :

                                          

 Ta đặt Dd_M= d_1M - d_2M ; Dd_N = d_1N - d_2N, giả sử: Dd_M < Dd_N

Với số giá trị nguyên của k thỏa mãn biểu thức trên là số điểm (đường)  cần tìm giữa hai điểm M và N.

Chú ý: Trong công thức (10) Nếu M hoặc N trùng với nguồn thì không dùng dấu "="(chỉ dùng dấu < )  Vì nguồn là điểm đặc biệt không phải là điểm cực đại hoặc cực tiểu.

2. Dùng công thức bất phương trình:

Số cực đại và cực tiểu trên đoạn thẳng nối hai điểm M và N trong vùng có giao thoa (M gần S₁ hơn S₂ còn N thì xa S₁ hơn S₂) là số các giá trị của k (k Î z) tính theo công thức sau ( không tính hai nguồn):

                                             

Ta suy ra các công thức sau đây:

a.Hai nguồn dao động cùng pha: ( Dj = 0)

                      * Số Cực đại: \[\frac{{{S}_{1}}M-{{S}_{2}}M}{\lambda }\]< k < \[\frac{{{S}_{1}}N-{{S}_{2}}N}{\lambda }\]

                      * Số Cực tiểu: \[\frac{{{S}_{1}}M-{{S}_{2}}M}{\lambda }\]- \[\frac{1}{2}\]< k < \[\frac{{{S}_{1}}N-{{S}_{2}}N}{\lambda }\] - \[\frac{1}{2}\].

b.Hai nguồn dao động ngược pha: ( Dj = (2k+1)p )

                        * Số Cực đại: \[\frac{{{S}_{1}}M-{{S}_{2}}M}{\lambda }\]+ \[\frac{1}{2}\]< k < \[\frac{{{S}_{1}}N-{{S}_{2}}N}{\lambda }\]+ \[\frac{1}{2}\].

                         * Số Cực tiểu: \[\frac{{{S}_{1}}M-{{S}_{2}}M}{\lambda }\] < k < \[\frac{{{S}_{1}}N-{{S}_{2}}N}{\lambda }\].

c.Hai nguồn dao động vuông pha: ( Dj = (2k+1)p/2 )

                          * Số Cực đại: \[\frac{{{S}_{1}}M-{{S}_{2}}M}{\lambda }\]+ \[\frac{1}{4}\]< k < \[\frac{{{S}_{1}}N-{{S}_{2}}N}{\lambda }\]+\[\frac{1}{4}\].

                          * Số Cực tiểu: \[\frac{{{S}_{1}}M-{{S}_{2}}M}{\lambda }\]- \[\frac{1}{4}\]< k < \[\frac{{{S}_{1}}N-{{S}_{2}}N}{\lambda }\] - \[\frac{1}{4}\].

Nhận xét: số điểm cực đại và cực tiểu trên đoạn AB là bằng nhau nên có thể dùng 1 công thức

Số giá trị nguyên của k thoả mãn các biểu thức trên là số điểm ( đường) cần tìm

BÀI TẬP VÍ DỤ

1.Tìm số điểm dao động với biên độ cực đại hoặc cực tiểu giữa hai nguồn:

Bài 1:Trong một thí nghiệm về giao thoa sóng trên mặt nước, hai nguồn kết hợp S₁ và S₂  cách nhau 10cm dao động cùng pha và có bước sóng  2cm.Coi biên độ sóng không đổi khi truyền đi.

  a.Tìm số điểm dao động với biên độ cực đại, Số điểm dao động với biên độ cực tiểu quan sát được .

  b.Tìm vị trí các điểm dao động với biên độ cực đại  trên đoạn S₁S₂ .

Giải:  a.Vì các nguồn dao động cùng pha, Ta có số đường hoặc số điểm dao động cực đại: $-\frac{l}{\lambda }

     => $-\frac{10}{2}-5< k < 5.Suy ra: k = 0; ± 1;±2 ;±3; ±4 .=> có 9 số điểm (đường) dao động cực đại

-Ta có số đường hoặc số điểm dao động cực tiểu:    $-\frac{l}{\lambda }-\frac{1}{2}

=> $-\frac{10}{2}-\frac{1}{2} -5,5< k < 4,5 . Suy ra: k = 0; ± 1;±2 ;±3; ±4; - 5 .

-Vậy có 10 số điểm (đường) dao động cực tiểu      

b. Tìm vị trí các điểm dao động với biên độ cực đại  trên đoạn S₁S₂

      - Ta có:  d₁+ d₂ = S₁S₂ (1) 

                    d₁- d₂  = S₁S₂ (2)

      -Suy ra: d₁ = $\frac{{{S}_{1}}{{S}_{2}}}{2}+\frac{k\lambda }{2}$   =$\frac{10}{2}+\frac{k2}{2}$ = 5+ k với  k = 0; ± 1;±2 ;±3; ±4

        -Vậy Có 9 điểm dao động với biên độ cực đại  trên đoạn S₁S₂ .

        -Khỏang cách  giữa  2 điểm dao động cực đại liên tiếp bằng l/2 = 1cm.

Bài 2:Hai nguồn sóng cơ S₁ và S₂ trên mặt chất lỏng cách nhau 20cm dao động theo phương trình \[{{u}_{1}}={{u}_{2}}=4\cos 40\pi t\](cm,s) , lan truyền trong môi trường với tốc độ v = 1,2m/s .

1/ Xét các điểm trên đoạn thẳng nối S₁ với S₂ .

a. Tính khoảng cách giữa hai điểm liên tiếp có biên độ cực đại .

b. Trên S₁S₂ có bao nhiêu điểm dao động với biên độ cực đại .

2/ Xét điểm M cách S₁ khoảng 12cm và cách S₂ khoảng 16 cm. Xác định số đường cực đại đi qua đoạn S₂M.

Giải :

1a/ Khoảng cách giữa hai điểm liên tiếp có biên độ cực đại:  l = v.T =v.2p/w =  6 (cm)

- Hai nguồn này là hai nguồn kết hợp (và cùng pha) nên trên mặt chất lỏng sẽ có hiện tượng giao thoa nên các điểm dao động cực đại trên đoạn  l = S₁S₂ = 20cm  sẽ có : 

Khoảng cách giữa hai điểm liên tiếp cực đại thứ k và thứ (k+1) là : \[\Delta d={{d}_{1(k+1)}}-{{d}_{1k}}=\frac{\lambda }{2}\]= 3 (cm).

 Ghi nhớ:  Trên đoạn thẳng nối 2 nguồn , khoảng cách giữa hai cực đại liên tiếp bằng \[\frac{\lambda }{2}\]

1b/ Số điểm dao động với biên độ cực đại trên S₁S₂ :

Do các điểm dao động cực đại trên S₁S₂  luôn có : \[0<{{d}_{1}}® \[0<\frac{1}{2}k\lambda +\frac{1}{2}l

=> \[-3,33<> ® có 7 điểm dao động cực đại .

- Cách khác : áp dụng công thức tính số cực đại trên đoạn thẳng nối hai nguồn cùng pha :

  \[N=2\left[ \frac{l}{\lambda } \right]+1\] với \[\left[ \frac{l}{\lambda } \right]\]là phần nguyên của \[\frac{l}{\lambda }\] ®  N = 7

2/ Số đường cực đại đi qua đoạn S₂M:

 Giả thiết tại M là một vân cực đại , ta có : \[{{d}_{2}}-{{d}_{1}}=k\lambda \to k=\frac{{{d}_{2}}-{{d}_{1}}}{\lambda }=\frac{16-12}{6}\approx 0,667\]. => M không phải là vân cực đại mà M nằm trong khoảng vân cực đại số 0 và vân cực đại số 1=>trên  S₂M chỉ có 4 cực đại .

Bài 3:   Trong thí nghiệm giao thoa với hai nguồn phát sóng đồng bộ tại A, B trên mặt nước. AB = 9,4cm. Tại điểm M thuộc AB cách trung điểm của AB gần nhất một đoạn 0,5cm, mặt nước luôn đứng yên. Số điểm dao động cực đại trên AB có thể nhận giá trị nào sau

A.7                             B.19                           C.29                                   D.43

Giải :  Khoảng cách từ điểm đứng yên gần nhất đến trung điểm là 0,5cm tức là khoảng cách ngắn nhất giữa một cực đại và một cực tiểu là nửa bước sóng, suy ra bước sóng bằng 1cm

-Hai nguồn đồng pha, công thức tính số cực đại: $-\frac{l}{\lambda } -9,4

Bài 4:   Tại hai điểm A và B trên mặt chất lỏng cách nhau 10 cm có hai nguồn phát sóng kết hợp dao động theo phương trình u₁ = acos(10pt), u2 = bcos(10pt + p). Tốc độ truyền sóng trên mặt chất lỏng 20 (cm/s). Tìm số cực tiểu trên đoạn AB

A. 5                             B. 6                             C. 4                                 D. 3

Giải: Bước sóng l =v/f=20/5 =4(cm).Dùng công thức (2):  \[({{d}_{1}}-{{d}_{2}})=(\Delta {{\varphi }_{M}}-\Delta \varphi )\frac{\lambda }{2\pi }\]

Vì M nằm trên đường cực tiếu nên \[\Delta {{\varphi }_{M}}=(2k+1)\pi \] =>=>(d₁-d₂) = [ (2k+1)p-p]4/2p =4k mà – AB < d1-d2 < AB nên ta có -2,5 < k < 2,5 có 5 điểm cực tiểu

Bài 5: Hai nguồn sóng kết hợp A, B cách nhau 21cm dao động theo các phương trình u₁= acos(4pt), u₂ = bcos(4pt + p), lan truyền trong môi trường với tốc độ 12(cm/s).Tìm số điểm dao động cực đại trong khoảng AB

A. 7                             B. 8                            C. 6                                  D. 5

Giải: Bước sóng l =v/f=12/2 = 6(cm)  . Dùng công thức (2):  \[({{d}_{1}}-{{d}_{2}})=(\Delta {{\varphi }_{M}}-\Delta \varphi )\frac{\lambda }{2\pi }\]

Vì M nằm trên đường cực đại nên \[\Delta {{\varphi }_{M}}=2k\pi \] => \[({{d}_{1}}-{{d}_{2}})=(2k\pi -\pi )\frac{6}{2\pi }\]= 6k-3 mà – AB < d₁- d₂ < AB nên ta có -3 < k < 4 có 6 điểm cực đại

2.Tìm số điểm dao động với biên độ cực đại hoặc cực tiểu giữa hai điểm bất kỳ:

Bài 1:   Hai nguồn sóng cơ S₁ và S₂ trên mặt chất lỏng cách nhau 20cm dao động theo phương trình \[{{u}_{1}}=4\cos 40\pi t\](cm,s) và \[{{u}_{2}}=4\cos (40\pi t+\pi )\] , lan truyền trong môi trường với tốc độ v = 1,2m/s .

1/ Xét các điểm trên đoạn thẳng nối S₁ với S₂ .

a. Tính khoảng cách giữa hai điểm liên tiếp có biên độ cực đại .

b. Trên S₁S₂ có bao nhiêu điểm dao động với biên độ cực đại .

2/ Xét điểm M cách S₁ khoảng 20cm và vuông góc với S₁S₂ tại S₁ . Xác định số đường cực đại đi qua đoạn S₂M .

Giải :  

1a/ Khoảng cách giữa hai điểm liên tiếp có biên độ cực đại: 

  Khoảng cách giữa hai cực đại liên tiếp bằng \[\frac{\lambda }{2}\]®  Dd = 3 cm .

1b/ Số điểm dao động với biên độ cực đại trên S₁S₂ :

-  Từ (1) ®  \[{{d}_{1}}=\frac{1}{2}\left[ l-(k+\frac{1}{2})\lambda  \right]\] ; Do các điểm dao động cực đại trên S₁S₂  luôn có : \[0<{{d}_{1}}®\[0<\frac{1}{2}\left[ l-(k+\frac{1}{2})\lambda  \right] =>  \[-3,83® 6 cực đại

-  “Cách khác ”:  Dùng công thức \[N=2\left[ \frac{l}{\lambda }+\frac{1}{2} \right]\] trong đó \[\left[ \frac{l}{\lambda }+\frac{1}{2} \right]\] là phần nguyên của \[\left( \frac{l}{\lambda }+\frac{1}{2} \right)\].  

Ta có kết quả : \[N=2\left[ \frac{20}{6}+\frac{1}{2} \right]=6\] .

2/ Số đường cực đại đi qua đoạn S₂M

Sử dụng công thức \[{{d}_{2}}-{{d}_{1}}=(k+\frac{1}{2})\lambda \] , với : d₁ = l =20cm, \[{{d}_{2}}=l\sqrt{2}=20\sqrt{2}\]cm

Giả thiết tại M là một vân cực đại  , ta có \[{{d}_{2}}-{{d}_{1}}=(k+\frac{1}{2})\lambda \] ® 

k = 0,88 . Như vậy tại M không phải là cực đại , mà M nằm trong 

khoảng  từ cực đại ứng với k = 0 đến cực đại ứng với k = 1

® trên đoạn S₂M có 4 cực đại .

           

Bài 2:   Trong thí nghiệm giao thoa sóng trên mặt nước , Hai nguồn kết hợp A và B cùng pha . Tại điểm M trên mặt nước cách A và B lần lượt là d₁ = 40 cm  và d₂ = 36 cm dao động có biên độ cực đại . Cho biết vận tốc truyền sóng là v = 40 cm/s , giữa M và đường trung trực của AB có một cực đại khác .

1/ Tính tần số sóng .

2/ Tại điểm N trên mặt nước cách A và B lần lượt là d₁ = 35 cm  và d₂ = 40 cm dao động có biên độ như thế nào ? Trên đoạn thẳng hạ vuông góc từ N đến đường trung trực của AB có bao nhiêu điểm dao động với biên độ cực đại ?

Giải :

1/ Tần số sóng : Đề bài đã cho vân tốc v , như vậy để xác định được tần số  f  ta cần phải biết đại lượng bước sóng l mới xác định được f theo công thức \[f=\frac{v}{\lambda }\] 

• • Tại M có cực đại nên :  \[{{d}_{2}}-{{d}_{1}}=k\lambda \] (1)
  • Giữa M và đường trung trực có một cực đại khác ® \[\left| k \right|=2\]( Hay k = -2 ) (2)

    Vậy từ (1) và (2)® \[\lambda =\frac{40-36}{2}=\] 2 cm ;  Kết quả :  f = 20 Hz. 

2.Biên độ dao động tại N:

Tại N có \[{{d}_{2}}-{{d}_{1}}=40-35=5\]

®  \[{{d}_{2}}-{{d}_{1}}=(k+\frac{1}{2})\lambda \] với k = 2 . Như vậy tại N có biên độ dao động cực tiểu (đường cực tiểu thứ 3)

-  từ N đến H có 3 cực đại , ứng với k = 0 , 1, 2 .( Quan sát hình vẽ sẽ thấy rõ số cực đại từ N đến H)

Bài 5:    Trên mặt nước có hai nguồn kết hợp A và B cách nhau 8 cm, dao động theo phương trình lần lượt là u1 = acos(8pt), u2 = bcos(8pt). Biết tốc độ truyền sóng 4cm/s. Gọi C và D là hai điểm trên mặt nước sao cho ABCD là hình chữ nhật có cạnh BC = 6cm. Tính số điểm dao động với biên độ cực tiểu trên đoạn CD.

A. 8                 B. 9                 C. 10               D. 11

Giải:Bước sóng l =v/f=4/4 = 1(cm) 

 Dùng công thức (2): \[({{d}_{1}}-{{d}_{2}})=(\Delta {{\varphi }_{M}}-\Delta \varphi )\frac{\lambda }{2\pi }\]

Vì M nằm trên đường cực tiếu nên \[\Delta {{\varphi }_{M}}=(2k+1)\pi \]

=> (d₁-d₂) = [ (2k+1)p-0]1/2p =k+0,5. Áp dụng công thức: Dd_D £ \[({{d}_{1}}-{{d}_{2}})\]£  Dd_C :  AD--BD £ \[({{d}_{1}}-{{d}_{2}})\]£  AC--BC

Hay: – 4 £ d₁- d₂ £ 4 nên ta có - 4,5 £k £ 3,5 =>có 8 điểm cực tiểu   

 

Bài 6 (ĐH-2010):  Ở mặt thoáng của một chất lỏng có hai nguồn sóng kết hợp A và B cách nhau 20 cm, dao động theo phương thẳng đứng với phương trình \[{{u}_{A}}=2\cos 40\pi t\] và \[{{u}_{B}}=2\cos (40\pi t+\pi )\](  u_A và u_B tính bằng mm,  t tính bằng s). Biết tốc độ truyền sóng trên mặt chất lỏng là 30 cm/s. Xét hình vuông AMNB thuộc mặt thoáng chất lỏng. Số điểm dao động với biên độ cực đại trên đoạn BM là

     A. 19.                   B. 17.                           C. 20.                         D. 18.

Cách 1: Xét  điểm C trên MB là điểm dao động cực đại từ M đến B. Dùng công thức hai nguồn dao động ngược pha: (S₁ là A, S₂ là B, N  trùng với B )

* Số Cực đại: \[\frac{{{S}_{1}}M-{{S}_{2}}M}{\lambda }\]+ \[\frac{1}{2}\]< k < \[\frac{{{S}_{1}}N-{{S}_{2}}N}{\lambda }\]+ \[\frac{1}{2}\].

Số điểm dao động với biên độ cực đại trên đoạn MB :(N chính là B trùng với S₂ ,A là S₁) ta có :

* Số Cực đại: \[\frac{AM-BM}{\lambda }\]+ \[\frac{1}{2}\]< k < \[\frac{{{S}_{1}}{{S}_{2}}-{{S}_{2}}{{S}_{2}}}{\lambda }\]+ \[\frac{1}{2}\].

Thế số: \[\frac{20-20\sqrt{2}}{1,5}+\frac{1}{2}\prec k\prec \frac{20-0}{1,5}+\frac{1}{2}\]\[\Leftrightarrow -5,02\prec k\prec 13,8\]

Vì k nguyên nên k nhận các giá trị ,-5,-4,………,0,1,2,3….12,13: .Có tất cả 19 giá trị

Cách 2: Dùng công thức bất phương trình hai nguồn dao động ngược pha (S₁ là A , S₂ là B):

Xét  điểm C trên BM là  điểm dao động cực đại từ B đến M :

\[\frac{BB-AB}{\lambda }\]+ \[\frac{\Delta \phi }{2\pi }\]< k < \[\frac{BM-AM}{\lambda }\]+ \[\frac{\Delta \phi }{2\pi }\]

ð - 12,8 < k < 6,02; vì k Î Z nên k nhận 19 giá trị, do đó trên  BM có 19 cực đại.

 Cách 3: Dùng công thức tổng quát (10): Dd_M £ \[({{d}_{1}}-{{d}_{2}})=(\Delta {{\varphi }_{M}}-\Delta \varphi )\frac{\lambda }{2\pi }\]< Dd_B

Do 2 nguồn  dao đông ngược pha nên Dj = -p

Xét một điểm C trên MB là điểm dao động cực đại ta có Độ lệch pha của 2 sóng tại M: Dj_M = 2kp.

Thế vào công thức trên ta được: d₁-d₂=\[(2k+1)\frac{\lambda }{2}\].

Do C di chuyển từ M đến B nên vị trí của C được xác định như sau (Lúc đầu C ở M , lúc sau C ở B):

\[MA-MB\le {{d}_{1}}-{{d}_{2}}\prec BA-BB\to 20-20\sqrt{2}\le (2k+1)\frac{\lambda }{2}\prec 20\to -6,02\le k\prec 12,8\].

Vì k nguyên nên k nhận các giá trị -6,-5,-4,…,0,1,2,3….12: .Có tất cả 19 giá trị

 

Bài viết gợi ý: