BÀI TOÁN LÃI SUẤT
A. LÝ THUYẾT
1. Lãi đơn: là số
tiền lãi chỉ tính trên số tiền gốc mà không tính trên số tiền lãi do số tiền gốc
sinh ra, tức là tiền lãi của kì hạn trước không được tính vào vốn để tính lãi
cho kì hạn kế tiếp cho dù đến kì hạn người gửi không đến gửi tiền ra:
Công thức: Khách hang gửi vào ngân hàng A đồng với lãi đơn r% kì hạn thì số tiền
khách hàng nhận được cả vốn lẫn lãi sau n kì hạn.
\[{{S}_{n}}=A(1+nr)\]
2. Lãi kép: tiền lãi của kì hạn trước nếu người gửi không rút ra thì được tình vào vốn để tính cho kì hạn sau.
Công
thức: Khách hang gửi vào ngân hàng A đồng với lãi kép r% kì hạn thì số tiền
khách hàng nhận được cả vốn lẫn lãi sau n kì hạn.
\[{{S}_{n}}=A{{(1+r)}^{n}}\]
3. Tiền gửi
hàng tháng: Mỗi tháng gửi đúng cùng một số tiền vào 1 thời gian
cố định.
Công thức: Đầu mỗi tháng khách hàng gửi
vào ngân hàng số tiền A đồng với lãi kép r% tháng, thì số tiền khách hàng
nhận được cả vốn lẫn lãi sau n tháng ( nhận tiền cuối tháng, khi ngân hàng đã
tình lãi) là \[{{S}_{n}}\]
\[{{S}_{n}}=\frac{A}{r}\left[
{{\left( 1+r \right)}^{n}}-1 \right]\left( 1+r \right)\]
4. Gửi ngân hàng và rút tiền hằng tháng.
Công thức: Gửi ngân hàng số tiền A đồng
với lãi suất r% tháng. Mỗi tháng vào ngày ngân hàng tính lãi, rút ra số tiền là X đồng.
Tính số tiền còn lại sau n tháng là bao nhiêu
\[{{S}_{n}}=A{{(1+r)}^{n}}-X\frac{{{(1+r)}^{n}}-1}{r}\]
5. Vay vốn trả góp: Vay ngân hàng với số
tiền là A đồng với lãi suất r% tháng. Sau đúng một tháng kể từ ngày vay, bắt đầu hoàn
nợ; hai lần hoàn nợ cách nhau đúng 1 tháng, mỗi hoàn nợ số tiền là X đồng và trả
hết nợ sau đúng n tháng
\[{{S}_{n}}=A{{(1+r)}^{n}}-X\frac{{{\left(
1+r \right)}^{n}}-1}{r}\]
6. Bài toán tăng trưởng: Một người được lãnh lương khởi điểm là A đồng/ tháng. Cứ k tháng thì lương người đó được tăng
thêm r% / tháng. Hỏi sau n tháng người đó lãnh được tất cả số tiền là bao
nhiêu?
Công thức : Tổng số tiền nhận được
sau kn tháng là
\[{{S}_{kn}}=Ak\frac{{{\left( 1+r \right)}^{n}}-1}{r}\]
7.Bài toán tăng trưởng dân số:
Công thức \[S=A.{{e}^{n.r}}\]
Dân số ban đầu là A
n: sau n thời gian
r: Tỉ lệ tăng
S: Tổng số dân sau n năm
B. VÍ DỤ
VD1: Anh Nam vay tiền ngân hàng 1 tỷ đồng
theo phương thức trả góp( chịu lãi số tiền chưa trả) với lãi suất 0,5% /tháng. Cuối mỗi tháng bắt đầu từ tháng thứ
nhất anh Nam trả 30 triệu đồng. Hỏi sau bao nhiêu tháng anh Nam trả hết nợ?
A. 35 tháng B. 36 tháng
C. 37 tháng D. 38 tháng
Giải: Gọi a là số tiền vay, r là lãi, m là số tiền hằng tháng trả.
Áp dụng công thức vay vốn trả góp:
\[{{S}_{n}}=A{{(1+r)}^{n}}-X\frac{{{\left( 1+r \right)}^{n}}-1}{r}\]\[\Rightarrow
{{10}^{9}}{{(1+0.005)}^{n}}-{{30.10}^{6}}\frac{{{\left( 1+0.005
\right)}^{n}}-1}{0.005}=0\]\[\Rightarrow n\approx 36.55\]
Đáp án C
VD2: Ông A
cho ông B vay 1 tỉ đồng với lãi suất là \[0.5%\] hằng tháng theo hình thức tiền
lãi hằng tháng được cộng vào tiền gốc cho tháng kế tiếp. Sau 2 năm, ông B trả
cho ông A cả gốc lẫn lãi. Hỏi số tiền ông B cần trả là bao nhiêu? ( lấy làm
tròn đến hàng nghìn)
A. 3.225.100.000 B.
1.121.552.000
C. 1.127.160.000 D.
1.120.000.000
Giải: Tổng số tiền ông B cần trả sau 2 năm là 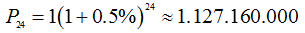
Đáp án C
VD3: Bạn An gửi số tiền tiết kiệm 58000000 đồng tron 8
tháng tại một ngân hàng thì nhận được 61329000 đồng. Khi đó lãi suất ngân hàng
là:
A.0.6% B. 6% C.0.7% D.7%
Giải: Lãi được tính theo công thức lãi kép, vì 8 tháng sau bạn an mới rút tiền.
Ta có công thức 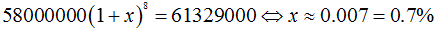
Đáp án C
VD4:
Biết rằng năm 2001, dân số việt nam là 78.685.800 người và tỉ lệ tăng dân số hằng
năm là 1.7%. Cho biết sự gia tăng dân số được ước tính theo công thức \[S=A.{{e}^{n.r}}\](
trong đó A là dân số của năm lấy tính làm mốc, S là dân số sau N năm, r là tỉ lệ
tăng dân số hằng năm). Nếu dân số vẫn tăng như tỉ lệ này thì đến năm nào thì
dân số nước ta là 120 triệu người
A.2026 B.2020 C.2022 D.2025
Giải: Ta có \[78685800.{{e}^{0.017.N}}=120000000\Rightarrow N\approx
24.8\]
Do đó tới năm 2026 thì dân số nước ta đạt mức 120 triệu người
Đáp án A
VD5: Một người vay ngân hàng 200 triệu đồng theo hình thức trả góp hằng
tháng, lãi suất ngân hàng cố định 0.8% tháng. Mỗi tháng người đó phải trả (
lần đầu tiên phải trả trước 1 tháng sau khi vay) một số tiền cố định không đổi
tới hết tháng 48 thì hết nợ. Tổng số tiền lãi người đó phải trả trong quá trình
nợ là bao nhiêu?
A. 38123000 đồng B.41641000
đồng C. 39200000 đồng D. 40345000 đồng
Giải:
Ta có công thức \[{{S}_{n}}=A{{(1+r)}^{n}}-X\frac{{{\left( 1+r
\right)}^{n}}-1}{r}\Rightarrow X\approx 41641000\]
Đáp án B
C. BÀI TẬP
TỰ LUYỆN
VD1: Theo dự báo với mức
tiêu thụ dầu không đổi như hiện nay thì trữ lượng dầu của nước A sẽ hết sau 100 năm nữa. Nhưng do
nhu cầu thực tế, mức tiêu thụ tăng lên 4% mỗi năm. Hỏi sau bao nhiêu năm nữa
thì số dầu dự trữ nước A sẽ hết?
A. 39 năm B. 40 năm C. 41 năm D. 42 năm
VD2: Một người mua điện
thoại với giá 18.500.500 đồng của một cửa hàng thế giới di động ngày 20/10
nhưng vì chưa đủ tiền nên quyết định mua theo hình thức trả góp mỗi tháng và trả
trước 5 triệu đồng trong 12 tháng, trả góp lần đầu tiên sau ngày mua một tháng
với lãi suất 3.4% tháng, Hỏi mỗi tháng sẽ phải tra cho công ty số tiền là bao
nhiêu?
A.1554000 đồng B. 1564000 đồng C. 1584000 đồng D.
1388824 đồng
VD3: Anh Nam mong muốn rằng
6 năm sau sẽ có 2 tỷ để mua nhà. Hỏi anh Nam phải gửi vào ngân hàng một khoản
tiền tiền tiết kiệm như nhau hằng năm gần nhất với giá trị nào sau đây, biết rằng
lãi suất của ngân hàng là 8% một năm và lãi hằng năm được nhập vào vốn
A. 253,5 triệu B. 251 triệu C. 253 triệu D. 252,5 triệu
VD4: Một người gửi ngân
hàng 50 triệu đồng với lãi suất 4% một tháng, sau một tháng tiền lãi được nhập
vào vốn. Hỏi sau một năm người đó rút tiền thì tổng số tiền nhận được là bao
nhiêu
A.\[50{{\left( 1,004 \right)}^{12}}\]triệu B.\[50{{\left(
1+12.004 \right)}^{12}}\]triệu C. \[50{{\left(
1+0,04 \right)}^{12}}\]triệu D. \[50.1,004\]triệu
VD5: Một người gửi vào ngân hàng với số tiền 20 triệu với lãi suất 1,65% /
quý( quý có 3 tháng) và không lấy lãi đến kì hạn lấy lãi. Hỏi sau bao lâu người
đó được 30 triệu ( cả vốn lẫn lãi) từ số vốn ban đầu?
A. 6 năm 3 quý B. 7 năm C. 6 năm 1 quý D. 6 năm 2 quý
VD6:
Một người mỗi tháng đều đặn gửi vào ngân hàng 1 khoản tiền T theo hình thức lãi
kép với lãi suất 0.6% mỗi tháng. Biết sau 15 tháng người đó có số tiền 10 triệu
đồng. Hỏi số tiền T gần nhất với giá trị nào nhất trong các số sau đây:
A. 635.000 đồng B. 645.000 đồng
C. 613.000 đồng D. 535.000 đồng
VD7:
Bạn An gửi tiết kiệm vào ngân hàng số tiền là 1 triệu đồng không kỳ hạn. Số tiền bạn nhận được sau 2 năm xấp xỉ bằng 1.250.000 đồng. Hỏi ;ãi suất của ngân hàng
A.0.9% B.
0.5% C. 0.65% D. 0.7%
VD8:
Bạn P gửi số tiền là 2 triệu đồng với kỳ hạn 3 tháng và lãi suất là 0.48% mỗi
tháng. Tính số tiền bạn nhận được sau 3 năm
A. 2380000 đồng B.
2420000 đồng C. 4230000 đồng D. 232000000 đồng
VD9:
Bà Lan gửi 10 triệu đồng vào
ngân hàng Viettin với lãi kép 5% /1 năm. Sau 2 năm số tiền mà thu được là?
A. \[10.{{(1+0,05)}^{2}}\] B.
\[10.{{(0,05)}^{2}}\] C. \[10.{{(1.0,05)}^{2}}\] D. \[10.(1+0,05)\]
VD10: Một
người gửi 15 triệu đồng vào ngân hàng theo thể thức lãi kép kỳ hạn một quý với
lãi suất 1,65% một quý. Hỏi sau bao lâu người đó có được ít nhất 20 triệu đồng
(cả vốn lẫn lãi) từ số vốn ban đầu? (Giả sử lãi suất không thay đổi).
A. 4 năm 1 quý. B. 4
năm 2 quý. C. 4 năm 3 quý. D. 5 năm.
ĐÁP ÁN
1C 2D 3D 4C 5C 6A 7C 8A 9A 10B







