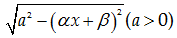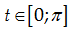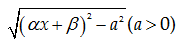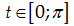CHUYÊN ĐỀ TÍCH PHÂN
A. LÝ THUYẾT
1. Định nghĩa: Cho
hàm số \[f(x)\]liên tục trên đoạn \[\left[ a;b \right]\]. Giả sử \[F(x)\] là một
nguyên hàm của \[f(x)\] trên đoạn \[\left[ a;b \right]\].
-Hiệu số \[F(b)-F(a)\] được gọi là tích
phân từ a đến b ( hay tích phân xác định trên đoạn \[\left[ a;b \right]\]) của hàm số
kí hiệu là \[\int\limits_{a}^{b}{f(x)dx}\]
-Ta còn dùng kí hiệu \[\left. F(x) \right|_{a}^{b}\]để chỉ hiệu số \[F(b)-F(a)\].
Vậy \[\int\limits_{a}^{b}{f(x)dx}=\left. F(x) \right|_{a}^{b}=F(b)-F(a)\]
-Ta gọi \[\int\limits_{a}^{b}{{}}\]là dấu tích phân, a là cận dưới, b là cận
trên, \[f(x)dx\]là biểu thức dưới dấu tích phân và \[f(x)\]là hàm số dưới dấu
tích phân.
- CHÚ Ý: Trong trường hợp a=
b, hoặc a>b, ta quy ước: \[\int\limits_{a}^{a}{f(x)dx=0};\int\limits_{a}^{b}{f(x)dx}=-\int\limits_{b}^{a}{f(x)dx}\]
2.Tính chất:
\[\int\limits_{a}^{b}{kf(x)dx}=k\int\limits_{a}^{b}{f(x)dx}\] \[\int\limits_{a}^{b}{\left[ f(x)\pm
g(x) \right]dx}=\int\limits_{a}^{b}{f(x)dx}\pm \int\limits_{a}^{b}{g(x)dx}\]
\[\int\limits_{a}^{b}{f(x)dx}=\int\limits_{a}^{c}{f(x)dx}+\int\limits_{c}^{b}{f(x)dx}\]
\[(a<>
*Dùng định nghĩa tích phân, ta chứng minh
được 2 tính chất sau:
-Nếu \[f(x)\ge 0\]trên \[\left[ a;b \right]\] thì \[\int\limits_{a}^{b}{f(x)dx\ge
0}\]
-Nếu \[f(x)>g(x)\]trên \[\left[ a;b \right]\] thì \[\int\limits_{a}^{b}{f(x)dx}\ge
\int\limits_{a}^{b}{g(x)dx}\]
3. Phương pháp tính tích phân
*Phương pháp phân tích, đưa về tích phân
đơn giản
– Phương pháp này tính được các tính phân hàm đa thức, hàm có chứa dấu trị
tuyệt đối, 1 số hàm lượng giác đơn giản.
– Để tính tích phân theo phương pháp này, cần phải
nắm định nghĩa tích phân, các tính chất tích phân và thuộc bảng nguyên hàm để
có thể biến đổi hàm dưới dấu tích phân về các hàm thường gặp
*Phương pháp dùng vi phân để tính tích
phân
Ta có thể trình bày gọn bằng công thức vi
phân \[dt\left( x \right)=t\left( x \right)dx\]. Cách làm này ngắn gọn, hiệu quả
trong rất nhiều bài toán tích phân.
\[\int\limits_{{}}^{{}}{f\left[
t(x) \right]dt(x)=\left. F\left[ t(x) \right] \right|_{a}^{b}}\]
* Phương pháp
tích phân từng phần
Cho hàm số \[f(x)\] có đạo hàm liên tục
trên K và 2 số thực a, b thuộc K, ta có:
\[\int\limits_{a}^{b}{u(x)v'(x)dx=}\left.
\left[ u(x)v(x) \right] \right|_{a}^{b}-\int\limits_{a}^{b}{v(x)u'(x)dx}\]. Viết
gọn \[\int\limits_{a}^{b}{udv}=\left. \left[ uv \right]
\right|_{a}^{b}-\int\limits_{a}^{b}{vdu}\]
* Phương pháp
biến đổi số dạng 1
– Đặt \[t=t\left( x \right)\]với là x là
biến ban đầu, t là biến mới. Khi đổi biến phải đổi cận.
+
Bb1: đặt \[x=x\left( t \right),\]suy ra \[dt=t'(x)dx\]
đổi cận \[x=a\Rightarrow
t=t(a)=\alpha ,x=b\Rightarrow t=t(b)=\beta \]
+ Bb2: biến đổi \[f(x)\]dx thành \[g(t)dt\]
+ Bb3: Khi đó \[\int{\frac{1}{\sqrt{{{x}^{2}}\pm
a}}dx=\ln \left| x+\sqrt{{{x}^{2}}\pm a} \right|+C}\]. Giả sử \[G(t)\] là một
nguyên hàm của \[g(t)\]thì \[I=\left. G(t) \right|_{\alpha }^{\beta }\]
* Phương pháp
biến đổi số dạng 2
|
Dạng |
\[f(x)\] |
Đặt |
Điều kiện |
|
1 |
\[\sqrt{1-{{x}^{2}}}\]
|
\[x=\sin t\] hoặc\[x=c\text{os}t\] |
\[t\in \left[ -\frac{\pi }{2};\frac{\pi }{2}
\right]\] |
|
2 |
\[\sqrt{{{x}^{2}}-1}\]
|
\[x=\frac{1}{\sin
t}\] hoặc \[x=\frac{1}{\text{cos}t}\] \[\alpha x+\beta
=\frac{a}{\sin t}\] hoặc \[\alpha x+\beta =\frac{a}{\text{cos}t}\] \[\] |
\[t\in \left[ -\frac{\pi }{2};\frac{\pi }{2} \right]\]/\[\left\{
0 \right\}\] |
|
3 |
\[\frac{1}{{{x}^{2}}+1}\];\[\sqrt{{{x}^{2}}+1}\] |
\[x=\tan t\]
|
\[t\in \left( -\frac{\pi }{2};\frac{\pi }{2} \right)\] |
– Đặt \[t=t\left(
x \right)\]với là x là biến ban đầu, t là biến mới. Khi đổi biến phải đổi cận.
+ Bb1: đặt \[x=x\left( t \right),\]suy ra \[dx=x'(t)dt\], đổi
cận \[x=a\Rightarrow t=\alpha ,x=b\Rightarrow t=\beta \]
+ Bb2: biến đổi \[f(x)\]dx thành \[g(t)dt\]
+ Bb3: Khi đó \[\int{\frac{1}{\sqrt{{{x}^{2}}\pm
a}}dx=\ln \left| x+\sqrt{{{x}^{2}}\pm a} \right|+C}\]. Giả sử \[G(t)\] là một
nguyên hàm của \[g(t)\]thì \[I=\left. G(t) \right|_{\alpha }^{\beta }\]
4.Một số lưu ý về phương pháp đổi biến số
- Các phép đổi biến sau
đây có thể xem là đổi biến dạng 1, cũng có thể xem là đổi biến dạng 2,
cách đặt \[t=t(x)\]hoặc \[x=x(t)\]rất
đơn giản, chẳng hạn: \[t=-x,t=\frac{\pi }{2}-x,t=\pi -x,...\]Các biến đổi thường gặp:
- Đổi biến với I để có \[I=\alpha
+\beta .I\Rightarrow I=\frac{\alpha }{1-\beta }\]thì \[\alpha ,\beta \in R,\beta \ne 1.\]
- Đổi biến
với I ta có \[2I=I+I=K\Rightarrow
I=\frac{1}{2}K\] với \[K\]là
tích phân đơn giản.
- Biến đổi I thành tổng \[I={{I}_{1}}+{{I}_{2}},\]
thực hiện phép biến đổi với \[{{I}_{1}}\] hay \[{{I}_{2}}\] ta được \[{{I}_{1}}=-{{I}_{2}}\]hay
\[{{I}_{1}}+{{I}_{2}}=K\] với \[K\]là tích phân đơn giản.
- Tích phân lẻ \[I=\int\limits_{-a}^{a}{f(x)dx}\] với a>0 \[f(x)\] là hàm lẻ trên đoạn \[\left[ -a;a
\right]\] tức là \[f(-x)=-f(x),\forall x\in \left[ -a;a \right]\]
- Tích
phân chẵn \[I=\int\limits_{-a}^{a}{\frac{f(x)}{{{k}^{x}}+1}}dx\], với a>0, \[k\in R\], \[f(x)\] là hàm chẵn trên đoạn \[\left[
-a;a \right]\] tức là \[f(-x)=f(x),\forall x\in \left[ -a;a \right]\]
-
Tích phân \[I=\int\limits_{0}^{a}{f(x)dx}\]
với \[a=\pi ,\frac{\pi }{2},...\] và \[f(x)\] có
chứa các hàm lượng giác
B.
BÀI TẬP
I.Ví
dụ
Vd1: Cho
phương trình \[\frac{1}{x}\int\limits_{1}^{x}{\ln tdt=\frac{x\ln
x-3}{x-1}},x>1\], phương
trình có nghiệm là :
A.\[x=4\] B.\[x=3\] C.\[x=\frac{7}{2}\] D. Kết quả khác.
Giải:
Bằng phương pháp tích phân từng phần ta có
\[\int\limits_{1}^{x}{\ln
tdt=x\ln x-x+1=\frac{x\ln x-x+1}{x-1}}=\frac{x\ln x-3}{x-1}\Rightarrow x=4\]
Đáp án A
Vd2: Xác định số a dương \[\int\limits_{0}^{a}{(x-{{x}^{2}})dx}\] để đạt giá trị lớn nhất
A.\[a=1\] B.\[a=\frac{1}{2}\]
C.\[a=2\] D.\[a=\frac{3}{2}\]
Giải:
Sử
dụng casio tìm giá trị lớn nhất của hàm số \[f(a)\], có \[f'(a)=a-{{a}^{2}}(a>0)\]
Đáp án A
Vd3:
Tìm
số nguyên dương k nhỏ nhất, thõa mãn \[\int\limits_{0}^{1}{\frac{dx}{2x+k}}\ge
0\]
A.\[k=3\] B. \[k=4\] C.\[k=1\] D.\[k=2\]
Giải: \[\forall k\in
{{N}^{*}},\forall x\in \left[ 0;1 \right],2x+k>0\]do đó \[\int\limits_{0}^{1}{\frac{dx}{2x+k}}>0,\forall
k\in {{N}^{*}}\]. Suy ra số nguyên dương k
nhỏ nhất thõa mãn là \[k=1\]
Đáp án C
Vd4:
Tìm \[x>1\] biết
rằng \[\int\limits_{1}^{x}{\ln tdt=1}\]
A.\[x=e\]
B.\[x={{e}^{2}}\] C.\[x={{e}^{3}}\] D.\[x=e+1\]
Giải:
Đặt 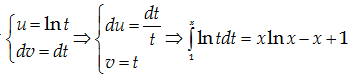
Vậy x thõa mãn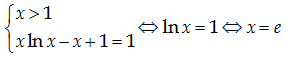
Đáp án A
Vd5:
Tính
tích phân \[I=\int\limits_{\frac{1}{a}}^{a}{\frac{({{x}^{4}}+{{x}^{-4}})lnxdx}{x},a>0}\]
A.\[1\] B.\[0\] C.\[2\operatorname{lna}\] D.\[\frac{\left(
{{a}^{2}}+1 \right)}{a}\ln a\]
Giải: Đặt \[u=\frac{1}{x}\Rightarrow
dx=-\frac{du}{{{u}^{2}}};\operatorname{lnx}=-lnu\] đổi cận
|
x |
\[a\] \[\frac{1}{a}\] |
|
u |
\[\frac{1}{a}\] \[a\] |
Vậy \[\int\limits_{a}^{\frac{1}{a}}{\frac{\left(
\frac{1}{{{u}^{4}}}+{{u}^{4}} \right)\left( -\ln u \right)\left( -\frac{du}{{{u}^{2}}}
\right)}{\frac{1}{u}}}=\int\limits_{a}^{\frac{1}{a}}{\frac{\left(
{{u}^{-4}}+{{u}^{4}} \right)\ln
udu}{u}}=-\int\limits_{\frac{1}{a}}^{a}{\frac{\left( {{u}^{-4}}+{{u}^{4}}
\right)\ln udu}{u}}=-I\Rightarrow I=0\]
Đáp
án B
II/BÀI TẬP TỰ LUYỆN
Câu
1: Tính
tích phân \[I=\int\limits_{0}^{1}{\frac{{{e}^{x}}(1+x)}{1+x{{e}^{x}}}}dx\]
A.\[I=\ln
\left( 1+{{e}^{2}} \right)\] B.\[I=\ln
\left( {{e}^{2}}-1 \right)\] C.\[I=\ln \left( 1+e \right)\] D.\[I=\ln \left( e-1 \right)\]
Câu 2: Tìm x \[\int\limits_{\frac{2}{\sqrt{3}}}^{x}{\frac{dt}{t\sqrt{{{t}^{2}}-3}}}=\frac{\pi
}{12}\]
A.\[x=2\sqrt{2}\] B.\[x=3\] C.\[x=2\] D.\[x=2\sqrt{2}\]
Câu 3: Biết tích phân \[\int\limits_{1}^{e}{\frac{\ln
x}{{{x}^{2}}}}dx=a-\frac{b}{e}(a,b\in N)\]. Giá trị \[a+b\]
A.
1 B.2 C.3 D.4
Câu 4: Biết tích phân \[\int\limits_{0}^{\pi
}{x\sin }x{{\cos }^{4}}xdx=\frac{a\pi }{b}(a,b\in N)\]. Giá trị \[a+b\]
A.
10 B. 6 C.15 D.16
Câu 5: Biết \[\int\limits_{0}^{\frac{\pi
}{2}}{\frac{\text{co}{{\text{s}}^{3}}x}{1+c\text{osx}}}dx=\frac{a\pi
-b}{c}(a,b,c\in N)\]. Giá
trị \[a+b+c\]
A.10 B.11 C. 15 D.
16
Câu 6: Biết \[\int\limits_{0}^{\frac{\pi
}{4}}{{{\tan }^{4}}}xdx=\frac{\pi }{a}-\frac{b}{c}(a,b,c\in N)\]. Giá trị \[a+b+c\]
A.
10 B.7 C.9 D.
4
Câu 7: Biết \[\int\limits_{0}^{\sqrt{3}}{\ln
\left( x+\sqrt{1+{{x}^{2}}} \right)}dx=\sqrt{a}\ln \left( 2+\sqrt{3}
\right)-b,(a,b,c\in N)\].
Giá
trị \[a+b+c\]
A.
10 B.7 C. 15 D.14
Câu 8: Biết \[\int\limits_{\frac{\pi
}{6}}^{\frac{\pi }{3}}{\frac{xdx}{\text{co}{{\text{s}}^{2}}x}}=\frac{a\pi
}{6\sqrt{3}}-\frac{\ln 3}{b}(a,b\in N)\]. Giá trị \[a+b\]
A.
10 B. 7 C. 15 D. 77
Câu 9:Biết \[\int\limits_{2}^{4}{\frac{{{x}^{2}}+1}{{{x}^{4}}-3{{x}^{2}}+1}}dx=\frac{a}{b}\ln
\frac{c}{d},(a,b,c,d\in N)\]. Giá trị \[a+b+c+d\]
A.
10 B. 6 C. 15 D.
77
Câu 10:Gọi S là tập hợp số nguyên dương k
thõa mãn điều kiện \[\int\limits_{1}^{e}{\ln \frac{k}{x}}dx
A. \[S=\left\{ 1;2;3 \right\}\] B. \[S=\left\{
1;2 \right\}\] C.
\[S=\left\{ 2;3 \right\}\] D.
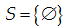
Đáp
án
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
C |
D |
C |
B |
C |
C |
D |
B |
D |
B |