HÀM SỐ
I.Các kiến kết quả quan trọng cần nắm để giải nhanh
1. Hàm số $y=a{{x}^{3}}+b{{x}^{2}}+cx+d$
$(y'=3a{{x}^{2}}+2bx+c)$ có 2 cực trị ↔ $\vartriangle
_{y}^{'}={{b}^{2}}-3ac>0$ . Khi đó, phương trình đường thẳng qua 2 điểm cực
trị là $y=(\frac{2c}{3}-\frac{2{{b}^{2}}}{9a})x+d-\frac{bc}{9a}$ .
2. Đồ thị hàm bậc ba luôn cắt trục
hoành tại ít nhất 1 điểm ( phương trình bậc ba luôn có ít nhất 1 nghiệm).
3. Đồ thị hàm bậc ba $y=a{{x}^{3}}+b{{x}^{2}}+cx+d$nhận
điểm uốn làm tâm đối xứng.
4. Hàm trùng phương $y=a{{x}^{4}}+b{{x}^{2}}+c$ có 3 cực trị khi
a, b trái dấu.
5. Đồ thị hàm trùng phương nhận trục
tung làm trục đối xứng.
6. Nếu đồ thi hàm trùng phương $y=a{{x}^{4}}+b{{x}^{2}}+c$
có 3 điểm cực trị thì 3 điểm này tạo thành tam giác cân tại đỉnh thuộc trục
tung.
7. Đồ thị của hàm trùng phương $y=a{{x}^{4}}+b{{x}^{2}}+c$cắt
trục hoành tại bốn điểm phân biệt, có hoành độ lập thành một cấp số cộng ↔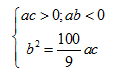
8.
Hàm số $y=\frac{ax+b}{cx+d}$ (có $y'=\frac{ad-bc}{{{(cx+d)}^{2}}}$ ) luôn đồng
biến hoặc nghịch biến trên $(-\infty ;\frac{-d}{c})$ và $(-\frac{d}{c};+\infty
)$ .
9. Hàm số $y=\frac{ax+b}{cx+d}$
không có cực trị.
10. Đồ thị hàm số
$y=\frac{ax+b}{cx+d}$ nhận đường thẳng $x=-\frac{d}{c}$ làm tiệm cận đứng, đường
thẳng $y=\frac{a}{c}$ làm tiệm cận ngang.
11. Đồ thị hàm số
$y=\frac{ax+b}{cx+d}$ nhận giao điểm hai đường tiệm cận $I(\frac{-d}{c};\frac{a}{c})$
làm tâm đối xứng và khi đó không có tiếp tuyến của đồ thị hàm số qua I.
12. Tích hai khoảng
cách từ một điểm H bất kì thuộc đồ thị hàm số$y=\frac{ax+b}{cx+d}$ đến hai đường
tiệm cận của nó là một số không đổi và bằng $\left| \frac{bc-ad}{{{c}^{2}}}
\right|$ .
13. Đường thẳng
y = mx + n cắt đồ thị hàm số $y=\frac{ax+b}{cx+d}$ tại hai điểm M, N và cắt hai
tiệm cân của đồ thị hàm số đó tại A, M thì ta có MA = NB.
14. Đồ thị hàm số
$y=\frac{a{{x}^{2}}+bx+c}{dx+e}$ có tiệm cận đứng là đường thẳng $x=-\frac{e}{d}$ và tiệm cận xiên là đường thẳng $y=\frac{a}{d}x+\frac{bd-ae}{{{d}^{2}}}$
.
15. Đồ thị hàm số
Đồ thị hàm số $y=\frac{a{{x}^{2}}+bx+c}{dx+e}$ nhận giao điểm $I(-\frac{e}{d};\frac{bd-2ae}{{{d}^{2}}})$
của hai tiệm cận làm tâm đối xứng.
16. Đường thẳng
đi qua các điểm cực đại và cực tiểu của đồ thị hàm số $y=\frac{a{{x}^{2}}+bx+c}{dx+e}$
có phương trình là $y=\frac{2ax+b}{d}$ .







