
CHUYÊN ĐỀ: ỨNG DỤNG NGUYÊN HÀM TÍCH PHÂN
·
Ứng dụng 1: Tính diện tích hình phẳng:
1. Diện
tích hình phẳng được giới hạn bởi 1 đường cong:
a) a) Lý thuyết:
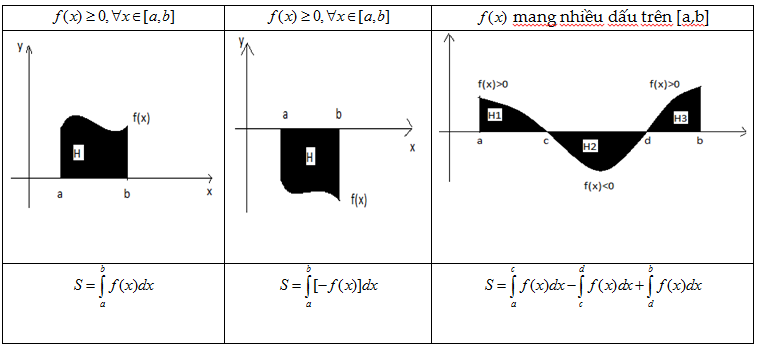
Nếu có hình phẳng giới hạn bởi các đường 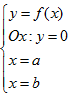
(\[f(x)\] liên tục trên [a,b]) thì \[S=\int\limits_{a}^{b}{\left| f(x) \right|dx}\]
a) b) Ví dụ
minh họa:
Câu 1: Diện tích hình phẳng được giới hạn bởi các dường
\[y={{x}^{2}}-2x,y=0,x=-1,x=2\]
Giải: \[S=\int\limits_{-1}^{2}{\left| {{x}^{2}}-2x
\right|}dx=\frac{8}{3}\]
Câu 2:
Diện tích hình phẳng giới hạn bởi đường cong (C) \[y=-{{x}^{3}}+3{{x}^{2}}-2\]
, hai trục tọa độ và đường thẳng \[x=2\]
Giải: \[S=\int\limits_{0}^{2}{\left| -{{x}^{3}}+3{{x}^{2}}-2
\right|dx}=\frac{5}{2}\]
2. Diện
tích hình phẳng được giới hạn bởi 2 đường cong:
a) Lý
thuyết:
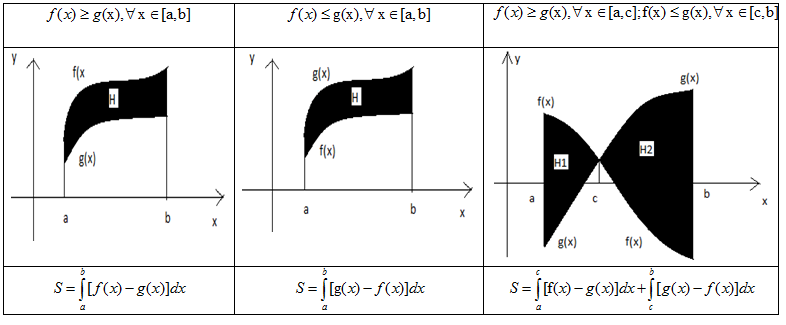
Nếu có hình phẳng giới hạn bởi các đường
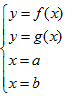
(\[f(x),g(x)\]liên tục trên
[a,b]) thì \[S=\int\limits_{a}^{b}{\left|
f(x)-g(x) \right|dx}\]
b) Ví
dụ minh họa:
Câu 1: Diện tích hình phẳng giới hạn bởi các đồ thị
hàm số \[y={{e}^{x}},y={{e}^{-x}},x=1\] \[y={{e}^{x}},y={{e}^{-x}},x=1\]
Giải:
Giao điểm phương trình hoành độ
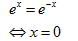
\[\Rightarrow S=\int\limits_{0}^{1}{\left| {{e}^{x}}-{{e}^{-x}}
\right|dx=\left| \int\limits_{0}^{1}{({{e}^{x}}-{{e}^{-x}})dx}
\right|}=\frac{{{e}^{2}}-2e+1}{e}\]
Câu 2: Diện tích hình phẳng giới hạn bời các đường
cong \[y={{x}^{2}}+2x,y=x+6\]
Giải:
Giao
điểm phương tình hoành độ:
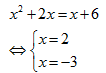
\[S=\int\limits_{-3}^{2}{\left| ({{x}^{2}}+2x)-(x+6)
\right|dx}=\frac{125}{6}\]
CHÚ Ý: Đối
với tích phân có chứa dấu trị tuyệt đối thì ta có 2 hướng giải quyết nhưng đều
phải tìm nghiệm của f(x) trước, tùy bài thì tách thành nhiều tích phân. Phá trị
tuyệt đối hoặc đưa trị tuyệt đối ra ngoài.
3. Bài tập
luyện thêm:
Câu 1: Diện
tích hình phẳng giới hạn bởi các đường \[y={{x}^{3}}-3x,y=x,x=-2,x=2\]
Câu 2: Diện tích hình phẳng giới hạn bởi các đường \[y={{x}^{3}},y=4x,x=0,x=3\]
Câu 3: Diện
tích hình phẳng giới hạn bởi các đường \[y=-\frac{1}{3}{{x}^{3}}+{{x}^{2}}-\frac{2}{3},y=0,x=2,x=0\]
Câu 4: Diện
tích hình phẳng giới hạn bởi các đường \[y=\sin
x,y=\cos x(0\le x\le \frac{\pi }{2})\]với trục Ox
Câu 5: Diện tích hình phẳng giới hạn
bởi các đường \[y=\frac{-x-2}{x-1},y=0,x=-1,x=0\]
Đáp án:
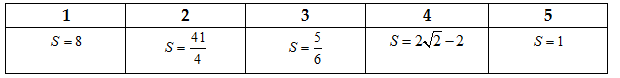
·
Ứng dụng 2: Tính thể tích khối tròn xoay:
1. 1.
Quay
quanh trục Ox:
a)
Lý
thuyết:
-
Cho
hình phẳng giới hạn bởi các đường 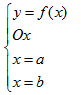
(
f(x) liên tục trên đoạn [a,b]), quay
quanh trục Ox, ta được khối tròn xoay)
-
Khi
đó thể tích V của khối tròn xoay được tính theo công thức sau:\[{{V}_{x}}=\pi
\int\limits_{a}^{b}{{{[f(x)]}^{2}}dx}\]
b)
Ví dụ minh họa:
Câu 1: Cho hình phẳng (H) giới hạn bởi các đường \[y=\sin
x,y=0,x=0,=\pi \]. Thể tích sinh bởi hình (H) quay quanh
Ox bằng
Giải: \[V=\pi \int\limits_{0}^{\pi
}{{{\left( \sin x \right)}^{2}}dx}=\frac{{{\pi }^{2}}}{2}\]
Câu 2: Cho hình phẳng (D) giới hạn bởi các đường \[y=\tan
x,x=0,x=\frac{\pi }{3},y=0\] . Thể tích
sinh bởi hình (D) quay quanh Ox bằng
Giải: \[V=\pi
\int\limits_{0}^{\frac{\pi }{3}}{{{\left( \tan x \right)}^{2}}dx=\pi \left(
\sqrt{3}-\frac{\pi }{3} \right)}\]
2.
2. Quay
quanh trục Oy:
a)
Lý
thuyết:
-
Cho
hình phẳng giới hạn bởi các đường 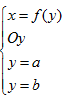
( f(y) liên tục trên đoạn [a,b]), quay quanh trục
Oy, ta được khối tròn xoay)
-
Khi
đó thể tích V của khối tròn xoay được tính theo công thức sau: \[{{V}_{y}}=\pi
\int\limits_{a}^{b}{{{[f(y)]}^{2}}dy}\]
b)
Ví
dụ minh họa:
Đề: Cho hàm số \[y=4-{{x}^{4}}\] có đồ thị (C), khối tròn xoay tạo
thành khi quay hình phẳng giới hạn bởi (C) và trục Ox, quay quanh Oy có thể
tích là:
Giải:
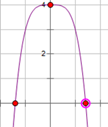
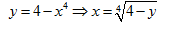
Giao điểm phương trình hoành độ
\[\sqrt[4]{4-y}=0\Rightarrow y=4\]
\[V=\pi
\int\limits_{0}^{4}{{{\left( \sqrt[4]{4-y} \right)}^{2}}dy}=\pi
\int\limits_{0}^{4}{\sqrt{4-y}dy=\frac{16\pi }{3}}\]
1. 3. Nhiều đồ thị quay quanh 1 trục nào đó:
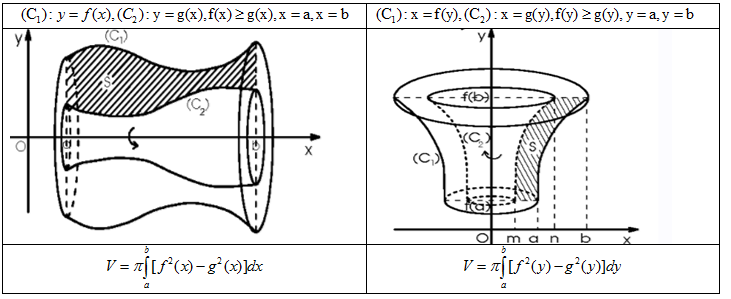
1. 4. Bài tập luyện thêm:
Câu 1: Thể
tích vật thể tròn xoay khi quanh hình phẳng giới hạn bởi các đường \[y=\ln
x,y=0,x=e\] xoay quanh trục Ox là?
Câu 2: Thể
tích vật thể tròn xoay khi quanh hình phẳng giới hạn bởi các đường \[y=\sqrt{x},y=x\]
Câu 3: Cho
hình phẳng (D) giới hạn bởi 2 trục Ox, Oy và đường thẳng \[y=3x+2\]. Thể tích sinh bởi hình (D) quay quanh
Oy bằng
Câu 4: Thể tích khối tròn xoay tạo thành khi quay quanh trục hoành hình phẳng giới hạn bởi các đường \[y=\frac{{{x}^{3}}}{3},y={{x}^{2}}\]
Câu 5: Thể
tích V của khối tròn xoay tạo thành khi cho miền phẳng D giới hạn bởi các đường
\[y=\frac{\sqrt{\ln (ex)}}{x},y=0,x=1,x=e\] quay quanh trục Ox bằng
Đáp án:
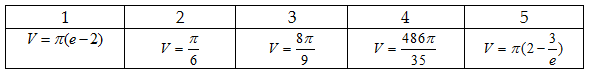
CHÚC CÁC BẠN HỌC THẬT TỐT NHÉ ^^







