Cực trị hàm số

CỰC TRỊ CỦA HÀM SỐ

I. Tóm tắt lý thuyết

1. Khái niệm cực trị hàm số

Giả sử hàm số \[f\] xác định và liên tục trên khoảng (a;b) và điểm \[{{x}_{0}}\] ∈ (a;b)

a) \[{{x}_{0}}\] được gọi là một điểm cực đại của hàm số \[f\] nếu \[f(x)\]<\[f({{x}_{0}})\] với mọi

\[x\] ∈ (a;b) ∖ {\[{{x}_{0}}\]} . Khi đó \[f({{x}_{0}})\] được gọi là giá trị cực đại của hàm số \[f\].

b) \[{{x}_{0}}\] được gọi là một điểm cực tiểu của hàm số \[f\] nếu \[f(x)\]>\[f({{x}_{0}})\] với mọi

\[x\] ∈ (a;b) ∖ {\[{{x}_{0}}\]} . Khi đó \[f({{x}_{0}})\] được gọi là giá trị cực tiểu của hàm số \[f\].

Điểm \[M({{x}_{0}};f({{x}_{0}}))\] được gọi là điểm cực đại (điểm cực tiểu) của đồ thị hàm số.

Các điểm cực đại và cực tiểu được gọi chung là điểm cực trị. Giá trị cực đại (giá trị cực tiểu) còn gọi là cực đại (cực tiểu) và được gọi chung là cực trị của hàm số.

2. Điều kiện cần để hàm số đạt cực trị

∎ Định lý 1: Nếu hàm số y=\[f(x)\]có đạo hàm trên khoảng (a;b) và đạt cực đại hoặc cực tiểu tại \[{{x}_{0}}\] thì \[f'({{x}_{0}})\]=0

Chú ý:

Đạo hàm \[f'\]có thể bằng 0 tại điểm \[{{x}_{0}}\] nhưng hàm số \[f\] không đạt cực trị tại điểm\[{{x}_{0}}\].

Hàm số có thể đạt cực trị tại một điểm mà tại đó hàm số không có đạo hàm.

3. Điều kiện đủ để hàm số đạt cực trị

∎ Đinh lí 2: Nếu hàm số \[f\] xác định và liên tục trên khoảng (a;b) và điểm \[{{x}_{0}}\] ∈ (a;b), có đạo hàm trên các khoảng (a;\[{{x}_{0}}\]) và (\[{{x}_{0}}\];b). Khi đó:

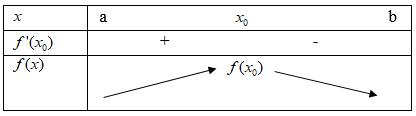
∗ Nếu \[f'({{x}_{0}})\]>0 trên khoảng (a;\[{{x}_{0}}\]) và \[f'({{x}_{0}})\]<0 trên khoảng (\[{{x}_{0}}\];b) thì \[{{x}_{0}}\] là một điểm cực đại của hàm số \[f(x)\].

Nói một cách khác, nếu \[f'({{x}_{0}})\]đổi dấu từ dương sang âm khi \[x\] đi qua điểm \[{{x}_{0}}\] thì hàm số đạt cực đại tại \[{{x}_{0}}\].

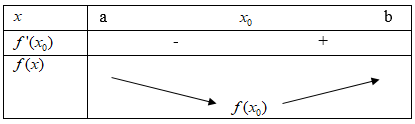
∗ Nếu \[f'({{x}_{0}})\]<0 trên khoảng (a;\[{{x}_{0}}\]) và \[f'({{x}_{0}})\]>0 trên khoảng (\[{{x}_{0}}\];b) thì \[{{x}_{0}}\] là một điểm cực tiểu của hàm số \[f(x)\].

Nói một cách khác, nếu \[f'({{x}_{0}})\]đổi dấu từ âm sang dương khi \[x\] đi qua điểm \[{{x}_{0}}\] thì hàm số đạt cực tiểu tại \[{{x}_{0}}\].

4. Quy tắc tìm cực trị

Ta thừa nhận định lý sau:

∎ Định lý 3: Giả sử hàm số \[f\]có đạo hàm cấp hai trên khoảng (a;b), với \[{{x}_{0}}\] ∈ (a;b). Khi đó:

a) Nếu \[f'({{x}_{0}})\]=0, \[f''({{x}_{0}})\]>0 thì \[{{x}_{0}}\] là điểm cực tiểu.

b) Nếu \[f'({{x}_{0}})\]=0, \[f''({{x}_{0}})\]<0 thì \[{{x}_{0}}\] là điểm cực đại.

∗QUY TẮC I: Áp dụng định lý 2

1. Tìm tập xác định.

2. Tính \[f'(x)\]. Tìm các điểm \[{{x}_{i}}\](\[i\]=1,2,3,…) tại đó \[f'(x)\]bằng 0 hoặc \[f'(x)\] không xác định.

3. Lập bảng biến thiên.

4. Xét dấu của \[f'(x)\], nếu \[f'(x)\] đổi dấu khi \[x\] qua điểm \[{{x}_{i}}\] thì hàm số đạt cực trị tại điểm \[{{x}_{i}}\].

∗QUY TẮC II: Áp dụng định lý 3

1. Tìm tập xác định.

2. Tính \[f'(x)\]. Tìm các điểm \[{{x}_{i}}\](\[i\]=1,2,3,…) của phương trình \[f'(x)\]=0.

3. Tính \[f''({{x}_{i}})\]

Nếu \[f''({{x}_{i}})\]<0 thì hàm số đạt cực đại tại \[{{x}_{i}}\].

Nếu \[f''({{x}_{i}})\]>0 thì hàm số đạt cực tiểu tại \[{{x}_{i}}\].

II. Bài tập minh họa

A. x=1 B. x=2 C. x=0 D. x=3

Hướng dẫn giải:

Ta có: \[y'=2x-4\]

\[y'=0=>x=2\]

Bảng biến thiên:

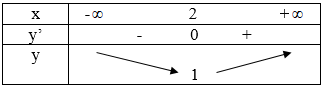
=> Đáp án A

A. 0 B. 1 C. 2 D. 3

Hướng dẫn giải:

Ta có: \[y'=-4{{x}^{3}}+4{{x}^{2}}\]=\[-4{{x}^{2}}(x-1)\]

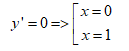
Bảng biến thiên:

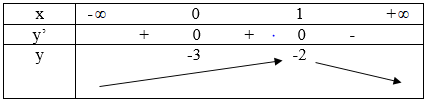
=> Hàm số có 1 điểm cực trị

(Chú ý: x=0 cũng là một nghiệm của đạo hàm nhưng qua x=0 đạo hàm không đổi dấu, do vậy x=0 không phải là cực trị của hàm số)

=> Đáp án B

A. 0 B. 1 C. 2 D. 3

Hướng dẫn giải:

Ta có: \[y'=\frac{(x-3)-(x+2)}{{{(x-3)}^{2}}}=\frac{-5}{{{(x-3)}^{2}}}\]

Bảng biến thiên:

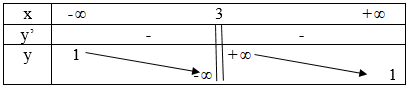
=> Hàm số không có điểm cực trị nào

=> Đáp án A.

A. x=0 B. x=1 xC. x=-1 D. x=\[\pm \]1

Hướng dẫn giải:

Ta có: \[y'=4{{x}^{3}}-4x=4x({{x}^{2}}-1)\]

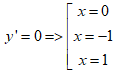
Cách 1:

Bảng biến thiên:

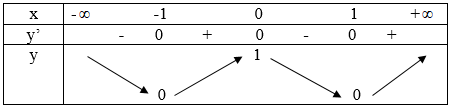
=> Hàm số đạt cực tiểu tại x=\[\pm \]1

Cách 2:

Ta có: \[y''=12{{x}^{2}}-4\]

\[y''(1)=y''(-1)=12-4=8>0\] => x=\[\pm \]1 là điểm cực tiểu của hàm số.

\[y''(0)=-4<0\] => x=0 là điểm cực đại của hàm số.

=> Đáp án D.

A. 2 B. 3 C. 4 D. 5

Hướng dẫn giải:

Xét hàm số \[f(x)={{x}^{3}}-\frac{3}{2}{{x}^{2}}-6x+4\]

Ta có:\[f'(x)=3{{x}^{2}}-3x-6\], \[f'(x)=0\] =>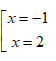

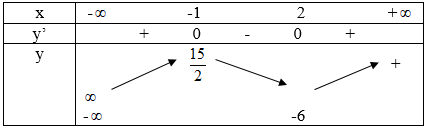
Bảng biến thiên:

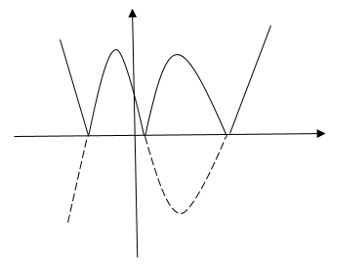
=> Đồ thị hàm số đã cho:

=> Hàm số đã cho có 5 điểm cực trị

=> Đáp án D.

A. x=4 B. y=4 C. x=1 D. x-2y+7=0

Hướng dẫn giải:

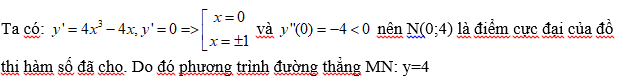
=> Đáp án B

III. Bài tập tự luyện

Bài 1: Đồ thị hàm số \[y={{x}^{3}}-3x\] có điểm cực đại là:

A. (-1;2) B. (-1;0) C. (1;-2) D. (1;0)

Bài 2: Cho hàm số \[f(x)=-{{x}^{4}}-4{{x}^{2}}+2\]. Chọn phát biểu đúng:

A. Hàm số trên có 1 điểm cực đại và 2 điểm cực tiểu.

B. Hàm số trên có 2 điểm cực đại và 1 điểm cực tiểu.

C. Hàm số có 1 điểm cực trị là điểm cực đại.

D. Hàm số có 1 điểm cực trị là điểm cực tiểu.

Bài 3: Cho hàm số \[y={{x}^{3}}-{{x}^{2}}-x+1\] (C). Khoảng cách từ O đến điểm cực tiểu của đồ thị hàm số là:

A. \[\sqrt{3}\] B. 2 C.\[\sqrt{\frac{1105}{729}}\] D. 1

Bài 4: Đồ thị hàm số \[y={{x}^{3}}-3{{x}^{2}}-9x+2\](C) có điểm cực đại, cực tiểu lần lượt là (\[{{x}_{1}};{{y}_{1}}\]) và (\[{{x}_{2}};{{y}_{2}}\]). Tính T=\[{{x}_{1}}{{y}_{2}}-{{x}_{2}}{{y}_{1}}\]

A. 4 B. -4 C. 46 D. -46

Bài 5: Trong các mệnh đề sau, hãy tìm mệnh đề sai ?

A. Hàm số \[y=\frac{1}{x+2}\] không có cực trị

B. Hàm số \[y=-{{x}^{3}}+3{{x}^{2}}-1\] có cực đại và cực tiểu

C. Hàm số \[y=x+\frac{1}{x+1}\] có hai cực trị

D. Hàm số \[y={{x}^{3}}+x+2\] có cực trị

Bài 6: Hàm số \[y=-{{x}^{4}}+2{{x}^{2}}-2\]:

A. Có một điểm cực trị. B. Có 3 điểm cực trị tạo thành tam giác vuông.

C. Có hai điểm cực trị D. Có 3 điểm cực trị tạo thành tam giác đều.

Bài 7: Hàm số \[y=\sqrt{{{x}^{2}}-x+1}\] đạt cực trị tại:

A. x=1 B. x=\[\frac{1}{2}\] C. x= -\[\frac{1}{2}\] D. x= -1

Bài 8: Hàm số \[y=\left| {{x}^{4}}-4{{x}^{2}}+2 \right|\] có bao nhiêu điểm cực trị: