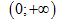CHUYÊN ĐỀ HÀM
SỐ MŨ VÀ LOGARIT
I. Hàm số mũ:
1. Định nghĩa:
·
Cho a là một số thực dương,
khác 1.
·
Hàm số y = \[{{a}^{x}}\]
được gọi là hàm số mũ cơ số a.
2.
Đạo hàm của hàm số mũ:
Ta có công thức:
\[\underset{u\to 0}{\mathop{\lim }}\,\frac{{{e}^{u}}-1}{u}=1.\] (1)
·
Định Lý 1:
Hàm số y = \[{{e}^{x}}\]
có
đạo hàm tại mọi x và
\[({{e}^{x}})'={{e}^{x}}\]
CHÚ Ý: Công
thức đạo hàm của hàm hợp đối với hàm số \[{{e}^{x}}\] (u=u(x)) có dạng \[({{e}^{u}})'=u'.{{e}^{x}}\]
·
Định Lý 2:
Hàm số y = \[{{a}^{x}}\]
(a
> 0, a\[\ne \]1) có đạo hàm
tại mọi x và
\[\left( {{a}^{x}} \right)'={{a}^{x}}.\ln a\]
CHÚ Ý: Đối với hàm hợp y = \[{{a}^{u\left( x
\right)}}\], ta có
\[\left( {{a}^{u}} \right)'={{a}^{u}}.u'.\ln
a\]
3. Khảo sát hàm logarit y = \[{{\log }_{a}}x\] (a > 0, a\[\ne \]1)

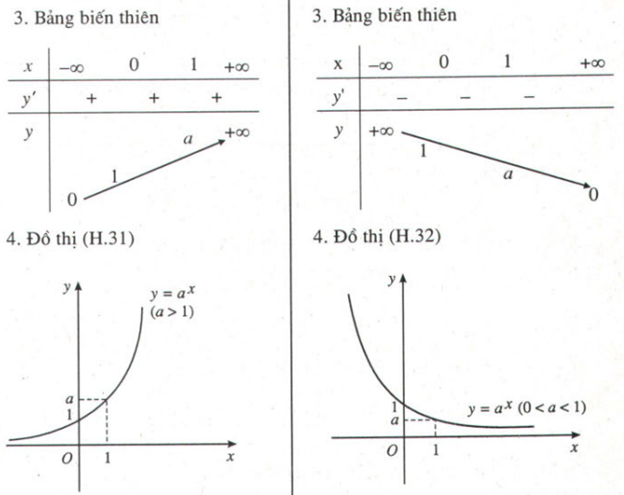
Bảng
tóm tắt các tính chất của hàm số mũ \[y={{a}^{x}}\]
|
Tập
xác định |
|
|
Đạo
hàm |
\[y'={{a}^{x}}\ln
x\] |
|
Chiều
biến thiên |
a>0:
Hàm số luôn đồng biến |
|
Tiệm
cận đồ thị |
Ox
là tiệm cận ngang |
|
Đồ
thị |
Đi
qua các điểm (0;1) và (1;a) nằm phía trên trục hoành (\[y={{a}^{x}}>0,\forall
x\exists R\]) |
II.
Hàm số mũ Logarit
1. Định nghĩa:
·
Cho a là một số thực dương,
khác 1.
·
Hàm số y = \[{{\log }_{a}}x\] được gọi là hàm số logarit cơ số a.
2.
Đạo hàm của hàm số Logarit:
·
Định Lý 3:
Hàm
số y = \[{{\log }_{a}}x\]
(a
> 0, a\[\ne \]1) có đạo hàm
tại mọi x>0 và
\[\left( {{\log
}_{a}}x \right)'=\frac{1}{x\ln a}\]
Đặc
biệt: \[(\ln x)'=\frac{1}{x}\]
CHÚ
Ý: Đối với hàm hợp \[y={{\log }_{a}}u(x)\], ta có \[{{\log
}_{a}}u=\frac{u'}{u\ln a}\]
3. Khảo sát hàm số logarit y = \[{{\log }_{a}}x\] (a > 0, a\[\ne \]1)

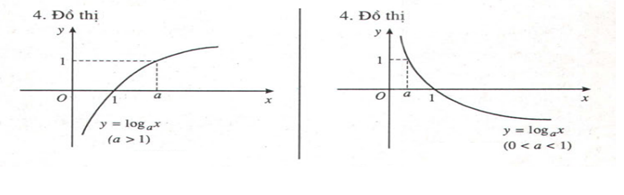
Bảng
tóm tắt các tính chất của hàm số y = \[{{\log }_{a}}x\]
|
Tập
xác định |
|
|
Đạo
hàm |
\[\left( {{\log }_{a}}x
\right)'=\frac{1}{x\ln a}\] |
|
Chiều
biến thiên |
a>0:
Hàm số luôn đồng biến |
|
Tiệm
cận đồ thị |
Oy
là tiệm cận đứng |
|
Đồ
thị |
Đi
qua các điểm (1;0) và (a;1) nằm phía bên phải trục tung |
Ví Dụ
VD1:
Tìm tập xác định của các hàm số
a,\[y={{(x+1)}^{3}}\]
b,\[y={{(2x-1)}^{-2}}\]
c,\[y={{(x+2)}^{\frac{1}{3}}}\]
HD:
a, Vì mũ dương nên TXD D= 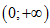
b, Vì mũ âm, nên y \[\ne \]0 \[\to \] TXD D= R/\[\left\{
\frac{1}{2} \right\}\]
c, Vì mũ không nguyên nên y > 0 (lưu ý nếu có
trong trắc nghiệm thì bạn không được dùng casio để thế đáp án vì có thể bị sai
ngay)
\[\to \] TXD
D= 
VD2: Hàm số \[y={{\log }_{2}}\left( x-1 \right)\] có tập xác định là:
HD: Hàm số xác định khi :x-1>0\[\to \] x>1. Vậy TXD D= 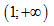
VD3: Cho phương trình \[2{{\log
}_{\sqrt{3}}}x-m+2=0\]. Xác
định m để phương trình có nghiệm \[x\in \left( \frac{1}{27};1 \right)\]
Bài
giải: \[2{{\log }_{\sqrt{3}}}x-m+2=0\]
\[\Leftrightarrow \] 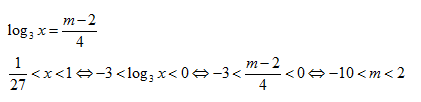
VD4: giải phương trình lnx.ln(x-1)=lnx
HD: Tập xác định x>1
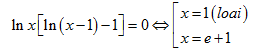
VD5:
Cho đẳng thức \[\frac{\sqrt[3]{a\sqrt[2]{a}}}{{{a}^{3}}}={{a}^{x}},0
Bài giải: \[\frac{\sqrt[3]{a\sqrt[2]{a}}}{{{a}^{3}}}=\frac{\sqrt[3]{{{a}^{2}}{{a}^{\frac{1}{2}}}}}{{{a}^{3}}}=\frac{\sqrt[3]{{{a}^{\frac{5}{2}}}}}{{{a}^{3}}}=\frac{{{a}^{\frac{5}{6}}}}{{{a}^{3}}}={{a}^{-\frac{13}{6}}}\] vậy x=\[-\frac{13}{6}\]
Bài tập tự luyện
Câu 1. Tập xác định của hàm số y = 2x−1 là
A.
D = R\{1}. B. D = R\{0}. C. D = R. D.D=(0;+∞).
Câu 2: Tìm
các khoảng nghịch biến của hàm số y = 3ln(x +1) + x - x2/2
A.(-1;
2) B. (2;
+∞) C. (-2 ;-1) và (2;
+∞) D. (-∞; -2) và (-1 ;2)
Câu 3: Cho
hai số thực a và b , với 0 < a < b < 1. Khẳng định nào sau đây là đúng
?
A.
logba < 1 < logab C. logab
< 1 < logba
B.
logba < logab < 1 D. 1 < logab
< logba
Câu 4: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = x3e-2x trên đoạn [-1; 4]

Câu 5: Số
lượng cá thể của một mẻ cấy vi khuẩn sau t ngày kể từ lúc ban đầu được ước
lượng bởi công thức N(t) = 1200.(1,148)t. Hãy tính số lượng cá thể
của mẻ vi khuẩn ở hai thời điểm: ban đầu và sau 10 ngày. Làm tròn kết quả đến
hàng trăm có kết quả là:
A.
1200 và 4700 cá thể C. 1200 và 1400 cá thể
B.
1400 và 4800 cá thể D. 1200 và 4800 cá thể
|
1 |
2 |
3 |
4 |
5 |
|
C |
B |
C |
C |
D |