ỨNG DỤNG TÍCH PHÂN
I/DiỆN tích hình phẲNG.
Cho 2 hàm số$y=f(x)$,
$y=g(x)$ liên tục trên đoạn $\left[ a;b \right]$
1. Diện tích S của miền giới hạn của $f(x)$ và trục
hoành 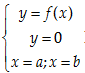

Để khử dấu trị tuyệt đối (ngoài cách dùng MTCT) ta thực
hiện:
*Cách 1:
Sử dụng định lý về dấu của nhị thức bậc nhất và định lý về
dấu của tam thức bậc hai để xét dấu các biểu thức $f(x)$
Chú ý: Nếu $f(x)$ không đổi dấu trên $\left[ a;b \right]$ ta
có $\int\limits_{b}^{a}{\left| f(x) \right|dx=\left|
\int\limits_{b}^{a}{f(x)dx} \right|}$
*Cách 2:
Dựa vào đồ thị của hàm số $y=f(x)$ trên đoạn $\left[ a;b
\right]$ để suy ra dấu của $f(x)$ trên đoạn đó
+ Nếu trên đoạn $\left[ a;b \right]$ đồ thị hàm số $y=f(x)$
nằm phía dưới trục hoành thì $f(x)\le 0,\forall x\in \left[ a;b \right]$
+ Nếu trên đoạn $\left[ a;b \right]$ đồ thị hàm số $y=f(x)$
nằm phía dưới trục hoành thì $f(x)\ge 0,\forall x\in \left[ a;b \right]$
+Nếu phương trình $f(x)=0$ có k nghiệm phân biệt ${{x}_{1}},{{x}_{2}},...,{{x}_{k}}$ thuộc $\left( a;b \right)$ thì trên mỗi
khoảng $\left( a;{{x}_{1}} \right);\left( {{x}_{1}};{{x}_{2}} \right);...\left(
{{x}_{k}};b \right)$ thì biểu thức $f(x)$ có dấu không đổi
2. Diện tích S của miền giới hạn của $f(x)$ và$g(x)$ 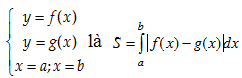
3. Diện tích S của miền giới hạn của $f(y)$ và$g(y)$ 
II/Thể tích khối tròn xoay.
Cho 2 hàm
số$y=f(x)$, $y=g(x)$ liên tục trên đoạn $\left[ a;b \right]$
1.Thể tích của khối
tròn xoay sinh ra khi quay miền giới hạn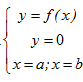
quanh Ox là : 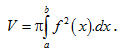
2. Thể tích của
khối tròn xoay sinh ra khi quay miền giới hạn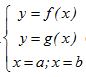
quanh Ox là : 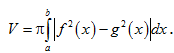
Chú ý:
+ Nếu $f(x)$ không đổi dấu trên đoạn $\left[
a;b \right]$thì $S=\int\limits_{a}^{b}{\left| f(x) \right|}dx=\left|
\int\limits_{a}^{b}{f(x)dx} \right|$.
+ Miền phẳng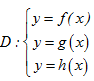
Khi đó
diện tích miền $D$ là: $S=\int\limits_{{{x}_{1}}}^{{{x}_{2}}}{\left|
f\left( x \right)-g\left( x \right)
\right|}dx+\int\limits_{{{x}_{2}}}^{{{x}_{3}}}{\left| h\left( x \right)-g\left(
x \right) \right|dx}$
IV.VÍ DỤ
VD 1: Diện tích S của hình phẳng giới hạn bởi đồ thị của
hai hàm số \[y=f\left( x \right)\,,\,y=g\left( x \right)\] liên tục trên $\left[
a;b \right]$và hai đường thẳng \[x=a\,,\,x=b\]:
A. \[S=\int\limits_{a}^{b}{\left| {{f}_{1}}\left( x
\right)-{{f}_{2}}\left( x \right) \right|dx}.\]
B. \[S=\left| \int\limits_{a}^{b}{\left( {{f}_{1}}\left( x
\right)-{{f}_{2}}\left( x \right) \right)dx} \right|.\]
C. \[S=\int\limits_{a}^{b}{\left[ {{f}_{1}}\left( x
\right)-{{f}_{2}}\left( x \right) \right]dx}.\]
D. \[S=\int\limits_{a}^{b}{{{f}_{1}}\left( x
\right)dx}-\int\limits_{a}^{b}{{{f}_{2}}\left( x \right)dx}.\]
Đáp án A
VD 2: Thể tích
khối tròn xoay được tạo thành khi quay quanh trục Ox hình phẳng được giới hạn
bởi các đường sau:\[y=f\left( x \right)\], trục Ox và hai đường thẳng \[x=a\,,\,x=b\]
$\left( a
A. \[V=\pi \int\limits_{a}^{b}{{{f}^{2}}\left( x
\right)dx}.\]
B. \[V=\int\limits_{a}^{b}{{{f}^{2}}\left( x \right)dx}.\]
C. \[V=\pi \int\limits_{a}^{b}{f\left( x \right)dx}.\]
D. \[V=2\pi \int\limits_{a}^{b}{{{f}^{2}}\left( x
\right)dx}.\]
Đáp án A
VD 3: Diện tích
hình phẳng được giới hạn bởi đồ thị của hàm số \[y={{x}^{2}}\] , trục
hoành và hai đường thẳng \[x=4,x=11\] là:
A.$\frac{1276}{3}$
B.$\frac{1267}{3}$
C.$\frac{46}{3}$
D.$\frac{59}{12}$
HD: 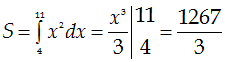
Đáp án B
VD
4: Thể tích khối tròn xoay sinh ra do quay hình phẳng giới hạn bởi các
đường $y={{x}^{3}}$, trục Ox, $x=-1$, $x=1$ quanh trục Ox là:
A.$\pi .$
B.$2\pi .$
C.$\frac{256\pi }{7}.$
D.$\frac{265\pi }{7}.$
HD: 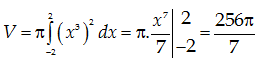
Đáp án C
VD 5: Diện tích
hình phẳng được giới hạn bởi các đường \[y={{x}^{3}}+3x\],\[y=-x\]
và đường thẳng \[x=-2\] là:
A. \[\frac{5}{99}.\]
B. \[12.\]
C. \[\frac{99}{5}.\]
D. \[\frac{1}{12}.\]
HD: Phương trình hoành độ giao điểm ${{x}^{3}}+3x=-x\Leftrightarrow
{{x}^{3}}+4x=0\Leftrightarrow x=0$
$S=\int\limits_{-2}^{0}{\left| {{x}^{3}}+3x+x \right|dx=12}$
Đáp án B
VD
6: Diện tích hình phẳng giới hạn bởi $y=-{{x}^{2}}+5x+6,y=0,x=0,x=2$ là:
A.\[\frac{58}{3}.\]
B.$\frac{56}{3}.$
C.$\frac{55}{3}.$
D.$\frac{52}{3}.$
$S=\int\limits_{0}^{2}{\left| -{{x}^{2}}+5x+6
\right|}dx=\frac{58}{3}$
Đáp án A
VD 7: Tính thể
tích khối tròn xoay giới hạn bởi các đường: $y=\sin x\,;Ox\,;\,x=0\,;\,x=\pi $
khi quay xung quanh trục \[Ox\]
A. $\frac{\pi }{2}.$
B. $\frac{{{\pi }^{2}}}{2}.$
C. $2\pi .$
D. ${{\pi }^{2}}.$
HD: $V=\pi \int\limits_{0}^{\pi }{{{\sin }^{2}}xdx}=\pi
\int\limits_{0}^{\pi }{\frac{1-\cos 2x}{x}dx=\frac{{{\pi }^{2}}}{2}}$
Đáp án B
VD 8: Diện tích
hình phẳng được giới hạn bởi đường cong $(C):y={{\sin }^{2}}x$, trục Ox và các
đường thẳng $x=0,x=\pi $ bằng:
A.$\pi .$
B.$\frac{\pi }{2}.$
C.$\frac{\pi }{3}.$
D.$\frac{\pi }{4}.$
HD: $S=\int\limits_{0}^{\pi }{{{\sin
}^{2}}xdx}=\int\limits_{0}^{\pi }{\frac{1-\cos 2x}{x}=\frac{\pi }{2}}$
Đáp án B
VD 9: Diện tích hình phẳng giới hạn bởi đồ thị
hàm số $y=-5{{x}^{4}}+5$ và trục hoành là:
A. 4.
B. 8.
C. 3108.
D. 6216.
HD: $-5{{x}^{4}}+5=0\Leftrightarrow
{{x}^{4}}=1\Leftrightarrow x=\pm 1$
$S=\int\limits_{-1}^{1}{\left| -5{{x}^{4}}+5 \right|dx}=8$
Đáp án B
V/ BÀI TẬP RÈN LUYỆN
Câu
1: Thể tích của khối tròn xoay khi quay quanh trục Ox hình phẳng được giới
hạn bởi đồ thị hàm số f(x) liên tục trên đoạn \[\left[ a;b \right]\], trục Ox
và hai đường thẳng\[x=a\,,\,x=b\] có công thức tính là:
A. \[V=\int_{a}^{b}{{{f}^{2}}}\left( x
\right)dx\].
B.\[V=\pi \int_{a}^{b}{{{f}^{2}}}\left(
x \right)dx\].
C. \[V=\pi \int_{a}^{b}{f}\left( x \right)dx\].
D. \[V=\pi \int_{a}^{b}{\left| f\left( x
\right) \right|}dx\].
Câu
2: . Diện tích S của hình phẳng giới hạn bởi đồ thị của
hàm số \[y=f\left( x \right)\] liên tục trên $\left[ a;b \right]$, trục hoành
và hai đường thẳng \[x=a\,,\,x=b\] được tính theo công thức:
A. \[S=\int\limits_{a}^{b}{\left| f\left( x \right)
\right|dx}.\]
B. \[S=\int\limits_{a}^{b}{f\left( x \right)dx}.\]
C. \[S=\int\limits_{a}^{0}{f\left( x
\right)dx}+\int\limits_{0}^{b}{f\left( x \right)dx}.\]
D. \[S=\int\limits_{a}^{0}{f\left(
x \right)dx}-\int\limits_{0}^{b}{f\left( x \right)dx}.\]
Câu 3: Cho
hai hàm số $f\left( x \right)$và $g\left( x \right)$ liên tục trên $\left[ a;b
\right]$ và thỏa mãn: $0
A. $V=\pi \int\limits_{a}^{b}{{{\left[ f\left( x
\right)-g\left( x \right) \right]}^{2}}dx}.$
B. $V=\pi \int\limits_{a}^{b}{\left[ {{f}^{2}}\left( x
\right)-{{g}^{2}}\left( x \right) \right]dx}.$
C. \[V={{\left\{ \pi \int\limits_{a}^{b}{\left[ f\left( x
\right)-g\left( x \right) \right]dx} \right\}}^{2}}.\]
D. $V=\int\limits_{a}^{b}{\left| f\left( x \right)-g\left( x
\right) \right|dx}.$
Câu
4: Thể tích của khối tròn xoay được giới hạn bởi các đường \[y=\sqrt{x.c\text{os
}x+{{\sin }^{2}}x}\] ,\[y=0,x=0,y=\frac{\pi }{2}\] là:
A. \[\frac{\pi \left( 3\pi -4
\right)}{4}\].
B. \[\frac{\pi \left( 5\pi +4
\right)}{4}\].
C. \[\frac{\pi \left( 3\pi +4
\right)}{4}\].
D. \[\frac{\pi \left( 3\pi +4
\right)}{5}\].
Câu
5: Thể tích khối tròn xoay khi quay quanh trục Ox hình phẳng giới hạn bởi $y=\ln
x,y=0,x=1,x=2$ là:
A.$2\pi {{\left( \ln 2-1 \right)}^{2}}.$
B.$2\pi {{\left( \ln 2+1 \right)}^{2}}.$
C.$\pi {{\left( 2ln2+1 \right)}^{2}}.$
D.x
Câu
6: Cho hình phẳng (H) được giới hạn bởi đường cong $(C):y={{x}^{3}}$, trục
Ox và đường thẳng $x=\frac{3}{2}$. Diện tích của hình phẳng (H) là :
A.$\frac{65}{64}.$
B.$\frac{81}{64}.$
C.$\frac{81}{4}.$
D.4.
Câu
7: Cho hình phẳng (H) được giới hạn bởi đường cong $(C):y={{e}^{x}}$, trục
Ox, trục Oy và đường thẳng $x=2$. Diện tích của hình phẳng (H) là :
A.$e+4.$
B.${{e}^{2}}-e+2.$
C.$\frac{{{e}^{2}}}{2}+3.$
D.${{e}^{2}}-1.$
Câu
8: Cho hình phẳng (H) được giới hạn bởi đường cong $(C):y=\frac{2x+1}{x+1}$,
trục Ox và trục Oy. Thể tích của khối tròn xoay khi cho hình (H) quay quanh
trục Ox là :
A.$3\pi .$
B.$4\pi \ln
2.$
C.$(3-4\ln
2)\pi .$
D.$(4-3\ln
2)\pi .$
Câu 9: Diện tích hình phẳng (phần bôi đen) trong hình sau được tích theo công thức:
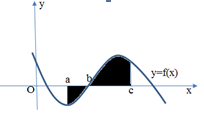
A.$S=\left| \int\limits_{a}^{b}{f\left( x \right)dx}
\right|+\left| \int\limits_{b}^{c}{f\left( x \right)}dx \right|$
B.$S=\left| \int\limits_{b}^{c}{f\left( x \right)dx}
\right|-\left| \int\limits_{a}^{b}{f\left( x \right)dx} \right|$
C.$\int\limits_{a}^{c}{f\left( x \right)dx}$
D. $S=\left| \int\limits_{a}^{c}{f\left( x \right)dx}
\right|$
Câu 10: Thể tích khối tròn xoay khi quay
quanh trục Ox hình phẳng giới hạn bởi các đường \[y=x\ln x,y=0,x=e\] có giá trị
bằng $\frac{\pi }{a}\left( b.{{e}^{3}}-2 \right)$ trong đó a, b là hai số thực
nào dưới đây?
A.$a=27,b=5.$
B. $a=24,b=6.$
C. $a=27,b=6.$
D. $a=24,b=5.$
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
B |
A |
B |
A |
A |
B |
D |
C |
A |
A |
.







