I.
Tính đơn điệu và dấu của đạo hàm :
1. Nhắc lại định
nghĩa :
- Hàm số y=\[f(x)\]đồng biến trên K nếu với mọi cặp \[{{x}_{1}},{{x}_{2}}\]thuộc
K mà \[{{x}_{1}}\]nhỏ hơn \[{{x}_{2}}\] thì \[f({{x}_{1}})\] nhỏ hơn \[f({{x}_{2}})\]tức
là : \[{{x}_{1}}\]<\[{{x}_{2}}\]\[\Rightarrow \]\[f({{x}_{1}})\]<\[f({{x}_{2}})\]
-
Hàm số y=\[f(x)\] nghịch biến trên K nếu với mọi cặp \[{{x}_{1}},{{x}_{2}}\]
thuộc K mà \[{{x}_{1}}\] nhỏ hơn \[{{x}_{2}}\] thì \[f({{x}_{1}})\]lớn hơn \[f({{x}_{2}})\],
tức là : \[{{x}_{1}}\]<\[{{x}_{2}}\]\[\Rightarrow \]\[f({{x}_{1}})\]>\[f({{x}_{2}})\]
- Hàm số đồng biến hoặc nghịch biến trên K được gọi chung là hàm số đơn điệu trên
K .
Ø Nhận xét :
·
Hàm số đồng biến : \[\frac{f({{x}_{2}})-f({{x}_{1}})}{{{x}_{2}}-{{x}_{1}}}\]
> 0 , \[\forall {{x}_{1}},{{x}_{2}}\in K\] \[({{x}_{1}}\ne {{x}_{2}})\];đồ
thị của hàm số đi lên từ trái sang phải
;
·
Hàm số nghịch biến : \[\frac{f({{x}_{2}})-f({{x}_{1}})}{{{x}_{2}}-{{x}_{1}}}\]
< 0 ,\[\forall {{x}_{1}},{{x}_{2}}\in K\]
\[({{x}_{1}}\ne {{x}_{2}})\]; đồ thị của hàm số đi xuống từ trái sang phải
.
2. Dấu của đạo
hàm :
Cho
hàm số y= \[f(x)\] có đạo hàm trên K .
-
Nếu \[f'(x)\] > 0 với mọi x thuộc K thì hàm số \[f(x)\]đồng biến trên K .
-
nếu \[f'(x)\] < 0 với mọi x thuộc K thì hàm số \[f(x)\]nghịch biến trên K .
\[\Rightarrow
f'(x)>0\]thì \[f(x)\]đồng biến và \[f'(x)<0\]thì \[f(x)\]nghịch biến
Chú
ý :
-
Nếu \[f'(x)\] = 0 , \[\forall x\in K\]thì f(x) không đổi trên K .
Ta
có định lý mở rộng :
Giả sử hàm số y=\[f(x)\]có đạo hàm trên K . Nếu \[f'(x)\ge 0\] (\[f'(x)\le 0\]) ,\[\forall x\in K\]và \[f'(x)\]= 0 chỉ tại một số hữu hạn điểm thì hàm số đồng biến (nghịch biến) trên K.
I.
Ví dụ minh họa :
1. Quy tắc
tính đơn điệu của hàm số :
-
Tìm tập xác định .
-
Tính đạo hàm \[f'(x)\], Tìm các điểm \[{{x}_{i}}\]( i= 1,2,…, n) mà tại đó đạo
hàm bằng 0 hoặc không xác định .
-
Săp xếp các điểm \[{{x}_{i}}\] theo thứ tự tăng dần và lập bảng biến thiên .
- Nêu kết luận về các khoảng đồng biến , nghịch biến của hàm số.
2. Áp dụng :
·
Ví dụ 1 : Xét sự đồng biến và nghịch biến của hàm số \[y=\frac{1}{3}{{x}^{3}}-2{{x}^{2}}+3x\]
Giải
-TXD
: D = R
-\[y'={{x}^{2}}+4x+3\]
- \[y'=0\Rightarrow
{{x}^{2}}-4x+3=0\]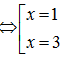
- Bảng biến thiên :
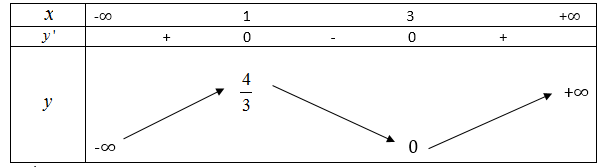
- Kết luận :
Hàm số
đồng biến trên khoảng (-∞;1) và (3;+∞).
Hàm số nghịch biến trên khoảng (1;3).
·
Ví dụ 2 :Tìm các
khoảng đồng biên scuar hàm số \[y={{x}^{4}}-2{{x}^{2}}-5\]
Giải
- TXD : D=R
- \[y'=4{{x}^{3}}-4x\]
\[y'=0\Leftrightarrow
4{{x}^{3}}-4x=0\]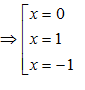
- Bảng biến thiên :
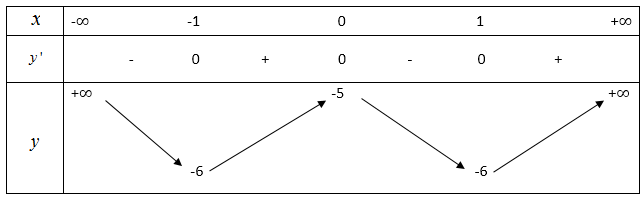
-
Kết luận
HÀm số đồng biến trên khoảng (-1;0) và (1; +∞).
Hàm số nghịch biến trên khoảng ( -∞;-1) và ( 0;1).
· Ví dụ 3 : Tìm m để hàm số \[y={{x}^{3}}+3{{x}^{2}}-3mx+10\]đồng
biến trên R.
Giải
- TXD : D=R
- Để hàm số
ĐB \[\Rightarrow y'\ge 0,\forall x\in D\]
\[\Leftrightarrow 3{{x}^{2}}+6x-3m\ge 0,\forall x\in D\]

- Vậy hàm số ĐB trên R \[\Leftrightarrow m\le -1\]
· Ví dụ 4 : Tìm m để
hàm số \[y=-\frac{1}{3}{{x}^{3}}+{{x}^{2}}-(m-3)x+\frac{11}{5}\] giảm trên R.
Giải
- TXD : D=R
- Để hàm số giảm ( NB) \[\Leftrightarrow y'\le 0\]
\[\Leftrightarrow -{{x}^{2}}+2x-m+3\le 0\]

- Vậy để hàm số NB trên R \[\Leftrightarrow m\ge 4\].
III. Bài tập :
1. Tìm các khoảng đồng biến của hàm số \[y=\frac{2{{x}^{2}}+x+1}{x+1}\]
:
A.(-∞;-1) và (0;+∞)
B.(-∞;-2)và (0;+∞)
C.(-2;-1)
và (-1;0)
D.(-∞;0) và (-1;0).
2. Đồ thị \[y={{x}^{4}}+8{{x}^{3}}-10\]\[\] giảm trên các khoảng nào ?
A.(-∞;-6)
B. (-6;0)
C. ( -5;2)
D.(-10;+∞)
3. Các khoảng đơn điệu của hàm số \[y=-{{x}^{3}}-3{{x}^{2}}+4\]
là :
A. Hàm số ĐB trên (-1;1) ; NB trên ( -∞;-1) và (1;+∞)
B. Hàm số ĐB trên (-3;0) và (1;+∞) ; NC trên ( -∞; -3) và ( 0;1)
C. Hàm số ĐB trên ( -2;0) ; NB trên ( -∞;-2) và ( 0;+∞)
D. Hàm số ĐB trên ( -∞;-2) và (0;+∞) ; NB trên ( -2;0)
4. Cho bảng biến thiên sau :

A. Hàm số ĐB trên R/(2;0)
B. Hàm số đồng biến trên khoảng (-∞;0)
C. Hàm số nghịch biến trên khoảng (-1;0)
D. Hàm số đồng biến trên khoảng (-∞;-1)
5. Trong các hàm số sau hàm số nào giảm
trên (-∞;+∞)
A.\[y={{x}^{4}}-4{{x}^{^{2}}}-5\]
B.\[y=4{{x}^{3}}-3{{x}^{2}}+x-3\]
C.\[y={{x}^{4}}+3{{x}^{2}}-4\]
D.\[y=-{{x}^{3}}-x+5\]
6. Tìm m để hàm số \[y=m{{x}^{3}}-2m{{x}^{2}}+12x-8\]tăng
trên R
A. 0 < m < 9
B. m < 0 và m >9
C. m < 5 và m >
D. 5 < m < 6
7. Cho bảng biến thiên sau :
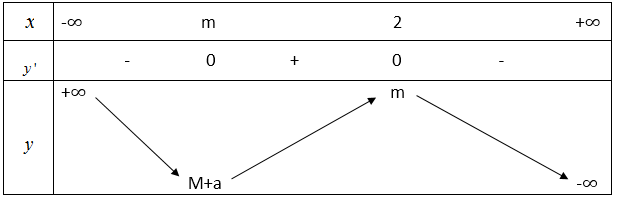
Tìm m và a để độ dài của đoạn thẳng đồ
thị tăng là \[2\sqrt{2}\]
A. m=1;a=2
B. m=4;a=1
C. m=0;a=2
D. m=2;a=4
8. Tìm m để hàm số \[y=-{{x}^{3}}-3{{x}^{2}}+mx+4\]nghịch
biến trên (1;+∞)
A.m < 9
B.m > 9
C.m ≥ 9
D.m ≤ 9
9. Tìm m để hàm số \[y=\frac{\sin
x+m}{\sin x-1}\]nghịch biến trên \[\left( \frac{\pi }{2};\pi \right)\]
A.m > 1
B.m < 1
C.m ≤ 1
D.m ≥ 1
10. Tìm tất cả các giá trị của tham số m
sao cho hàm số \[y=\frac{x-1}{x-m}\]đồng biến trên khoảng (-∞;0)
A.m > 1
B.0 ≤ m <1
C.-1 < m ≤ 0
D.m ≥ 0
Đáp án








