TIẾP TUYẾN VỚI ĐỒ THỊ CỦA HÀM SỐ
A/ LÝ THUYẾT
1/ Hệ số góc, phương trình tiếp tuyến
+ Hệ số góc
của tiếp tuyến tại $M({{x}_{0}};{{y}_{0}})$ là $k=y'({{x}_{0}})$
+ Phương
trình tiếp tuyến tại $M({{x}_{0}};{{y}_{0}})$ là $y=y'({{x}_{0}})(x-{{x}_{0}})+{{y}_{0}}$
a/ Tiếp tuyến tại điểm $M({{x}_{0}};{{y}_{0}})$
Tính ${{y}_{0}}$
=> $y'({{x}_{0}})$ => PTTT
Chú ý:
*Nếu đề bài
cho ${{x}_{0}}$ thì gọi điểm tiếp xúc là $M({{x}_{0}};{{y}_{0}})$ và tính ${{y}_{0}}=y'({{x}_{0}})$
*Nếu đề bài
chưa cho ${{x}_{0}};{{y}_{0}}$ thì gọi điểm tiếp xúc là $M({{x}_{0}};{{y}_{0}})$
và lập phương trình tiếp tuyến theo ${{x}_{0}}$
b/ Tiếp tuyến biết hệ số góc k
Gọi điểm tiếp
xúc $M({{x}_{0}};{{y}_{0}})$ . Tính y’, giải phương trình $y'({{x}_{0}})=k\Rightarrow
{{x}_{0}};{{y}_{0}}\Rightarrow $ Phương trình tiếp tuyến
Chú ý:
+ Tiếp tuyến
song song $\vartriangle \Rightarrow kT=k\vartriangle $
+ Tiếp tuyến
vuông góc $\vartriangle \Rightarrow kT=-1k\vartriangle $
B/ VÍ DỤ
VD 1: Đồ thị hàm số $y=\frac{{{x}^{3}}}{3}-2{{x}^{2}}+x+2$
có hai tiếp tuyến của (C) cùng song song với đường thẳng 2x + y – 5 = 0 là
A.$2x+y-\frac{10}{3}=0\And
2x+y-2=0$
B.$2x+y-4=0\And
2x+y-1=0$
C.$2x+y+\frac{4}{3}=0\And
2x+y+2=0$
D.$2x+y-3=0\And
2x+y+1=0$
HD:
Đường thẳng
2x + y – 5 = 0 có hệ số góc k = -2
$y'={{x}^{2}}-4x+1$
. Từ $y'=2\Leftrightarrow {{x}^{2}}-4x+1=-2\Leftrightarrow {{x}^{2}}-4x+3=0$
$=>{{x}_{1}}=1;{{y}_{1}}=\frac{4}{3}\Rightarrow
y=-2x+\frac{10}{3}$
${{x}_{1}}=3;{{y}_{1}}=-4\Rightarrow
y=-2x+2$
Đáp án A
VD 2: Đồ thị hàm số $y={{x}^{3}}-3{{x}^{2}}-3x$
có 2 tiếp tuyến cùng vuông góc với đường thẳng x + 6y – 6 = 0. Đó là các đường
thẳng
A.$y=6x+6\And
y=6x+12$
B.$y=6x-5\And
y=6x+27$
C.$y=6x+5\And
y=6x-27$
D.$y=6x-6\And
y=6x-12$
HD:
Đường thẳng
vuông góc với x + 6y – 6 = 0 có hệ số góc bằng 6
$y'=3{{x}^{2}}-6x-3$
$y'=6\Leftrightarrow
3{{x}^{2}}-6x-3=6\Leftrightarrow \Leftrightarrow 3{{x}^{2}}-6x-9=0$
${{x}_{1}}=-1\Rightarrow
{{y}_{1}}=-1\Rightarrow y=6x+5$
${{x}_{2}}=3\Rightarrow
{{y}_{2}}=-9\Rightarrow y=6x-27$
VD 3: Đồ thị hàm số $y={{x}^{3}}-3{{x}^{2}}+2$
có hai tiếp tuyến xuất phát từ điểm A(0;3). Đó là các đường thẳng
A.$y=3x+3\And
y=-4x+3$
B.$y=-3x+3\And
y=\frac{15}{4}x+3$
C.$y=4x+3\And
y=\frac{13}{4}x+3$
D.$y=-2x+3\And
y=\frac{5}{4}x+3$
HD:
Phương trình
tiếp tuyến có dạng y = kx + 3
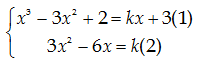
Thế (2) vào
(1):
${{x}^{3}}-3{{x}^{2}}+2=(3{{x}^{2}}-6x)x+3=3{{x}^{3}}-6{{x}^{2}}+3$
$\Leftrightarrow
2{{x}^{3}}-3{{x}^{2}}+1=0\Leftrightarrow {{(x-1)}^{2}}(2x+1)=0$
$\Leftrightarrow
x=1;k=-3\And x=-\frac{1}{2};k=\frac{15}{4}$
Hai tiếp tuyến
là $y=-3x+3\And y=\frac{15}{4}x+3$
Đáp án B
VD 4: Hàm số $y=f(x)=\frac{{{x}^{3}}}{3}-m{{x}^{2}}-6mx-9m+12$
có đồ thị (C). Khi tham số m thay đổi, các đồ thị (C) đều tiếp xúc với một đường
thẳng cố định. Đường thẳng này có phương trình
A.$y=-9x+9$
B.$y=9x+9$
C.$y=-9x+30$
D.$y=9x+30$
HD:
$y=\frac{{{x}^{3}}}{3}+12-m{{(x+3)}^{2}}\Rightarrow
\forall m,$ điểm $A(-3;3)\in (C)$
$y'={{x}^{2}}-2m(x+3)$
$y'(-3)=9$
Phương trình
tiếp tuyến tại A của (C) là
y = 9x + 30
Đáp án D
VD 5: Tiếp tuyến tại A(-3;-2) của đồ thị
hàm số (C): $y={{x}^{3}}+4{{x}^{2}}+4x+1$ cắt (C) tại M. Tọa độ của M là
A.M(1;10)
B.M(-2;1)
C.M(2;33)
D.M(-1;0)
HD:
$y'=3{{x}^{2}}+8x+4$
$y'(-3)=7$
Phương trình
tiếp tuyến của (C) tại A:
$y=7(x+3)-2\Leftrightarrow
y=7x+19$
Phương trình
hoành độ giao điểm:
${{x}^{3}}+4{{x}^{2}}+4x+1=7x+19$
$\Leftrightarrow {{x}^{3}}-4{{x}^{2}}-3x-18=0$ $\Leftrightarrow
{{(x+3)}^{2}}(x-2)=0$
$f(2)=33$ $\Rightarrow M(2;33)$
Đáp án C
VD 6: Cho hàm số $y=\frac{{{x}^{4}}}{2}-3{{x}^{2}}+\frac{3}{2}$
có đồ thị (C). Tiếp tuyến tại các điểm uốn của (C) có phương trình
A.$y=4x-3\And
y=-4x-3$
B.$y=-4x+3\And
y=4x+3$
C.$y=3x-4\And
y=-3x-4$
D.$y=-3x+4\And
y=3x+4$
HD:
\[y'=2{{x}^{3}}-6x\]
$y''=6{{x}^{2}}-6=0\Leftrightarrow
x=\pm 1$
$x=1\Rightarrow
y=1;y'(1)=-4\Rightarrow y=-4x+3$
$x=-1\Rightarrow
y=-1;y'(-1)=4\Rightarrow y=4x+3$
Đáp án B
C/ BÀI TẬP TỰ LUYỆN
Bài 1: Cho hàm số $y={{x}^{4}}-(m+5){{x}^{2}}+4$
có đồ thị (C). Để (C) tiếp xúc với đường thẳng y= -6x – 3 tại điểm có hoành độ ${{x}_{0}}=-1$
thì giá trị của m là
A.m = 6
B.m = 1
C.m = -6
D.m = -1
Bài 2: Cho hàm số $y=\frac{x-4m}{mx-4}$ có
đồ thị (H) với $m\ne 0;m\ne \pm 1$. (H) luôn đi qua hai điểm cố định A, B. Để
tiếp tuyến của (H) tại A và B song song với nhau, giá trị của m là
A.m = 2
B.m = -2
C.m = 3
D.m = 0
Bài 3: Cho hàm số $y=\frac{ax+b}{2x+3}$ có
đồ thị (C). Nếu (C) đi qua A(1;1) tại điểm $B\in (C)$ có hoành độ -2, tiếp tuyến
cảủa (C) có hệ số góc k = 5 thì các giá trị của a và b lần lượt là
A.2 ; 3
B.3 ; 2
C.2 ; -3
D.3 ; -2
Bài 4: Cho hàm số $y=\frac{(m+1)x+m}{x+m}$ có
đồ thị (H). Với mọi giá trị $m\ne 0$ (H) luôn tiếp xúc với một đường thẳng cố định.
Đường thẳng này có phương trình:
A.$y=-x+1$
B.$y=-x-1$
C.$y=x+1$
D.$y=x-1$
Bài 5: Cho hàm số $y=\frac{ax+2}{bx+3}$ có
đồ thị (H). Tại $M(-2;-4)\in (H)$ , tiếp tuyến của (H) song song với đường thẳng
7x – y + 5 = 0. Giá trị a và b lần lượt là
A.1 ; 2
B.2 ; 1
C.1 ; 3
D.3 ; 1
Bài 6: Hàm số $y=\frac{{{x}^{2}}-3x+4}{2x-2}$
có đồ thị (C). Tiếp tuyến với (C) tại A(0;-2) có phương trình
A.$x+2y-4=0$
B.$x+2y+4=0$
C.$x-2y-4=0$
D.$x-2y+4=0$
Bài 7: Hàm số $y=\frac{{{x}^{2}}+x}{2(x-1)}$
có đồ thị (C). Các tiếp tuyến của (C) song song với đường $y=-\frac{x}{2}+1$ là
A.$x+2y=0$
B.$x+2y+1=0$
C.$x+2y-1=0$
D.$x+2y+2=0$
Bài 8: Cho hàm số $y=\frac{{{x}^{2}}+3x+m}{x+1}$
có đồ thị (C). Để trên (C) có tiếp tuyến vuông góc với đường y = x + 1 thì m phải
thõa mãn
A.$m\ge 1$
B.$m\ge -1$
C.$m\ge 2$
D.$m\ge -2$
Bài 9: Hàm số $y=\frac{{{x}^{2}}+ax+b}{x+3}$
có đồ thị (C). Để tại $A\left( 0;-\frac{4}{3} \right)\in (C)$ , tiếp tuyến của (C) có hệ số góc bằng $\frac{10}{9}$
. Giá trị a; b lần lượt là
A.-2 ; -4
B.2 ; -4
C.-2 ; -4
D.4 ; -2
Bài 10: Hàm số $y=\frac{-x+3}{2x-1}$ có đồ
thị là (H). Tiếp tuyến của (H) song song với đường thẳng (d): 5x + 4y – 1 = 0
A.\[y=-\frac{5}{4}x+\frac{21}{8}\And
y=-\frac{5}{4}x-\frac{19}{8}\]
B.\[y=-\frac{5}{4}x-\frac{21}{8}\And
y=-\frac{5}{4}x+\frac{19}{8}\]
C.\[y=-\frac{5}{4}x+3\And
y=-\frac{5}{4}x-3\]
D.\[y=-\frac{5}{4}x+\frac{23}{8}\And
y=-\frac{5}{4}x-\frac{17}{8}\]
ĐÁP ÁN
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
C |
D |
B |
C |
B |
B |
A |
C |
B |
A |







