Bài Toán Tương Giao

BÀI TOÁN TƯƠNG GIAO

A/LÝ THUYẾT

Xét sự tương giao của hai hàm số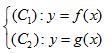

Số giao điểm của $({{C}_{1}})$ và $({{C}_{2}})$ là số nghiệm của phương trình $f(x)=g(x)$ . Khi đó bài toán chuyển về biện luận số nghiệm của phương trình $f(x)=g(x)$

Có hai trường hợp xảy ra:

+ Nếu (1) là phương trình trùng phương thì ta quy về phương trình bậc 2

+ Nếu (1) là phương trình bậc 3 hoặc bậc cao thì ta làm như sau:

-Nếu cô lập được m ta đưa phương trình trở thành $F(x)=h(m)$ thì bài toán quy về khảo sát hàm số $y=F(x)$

-Nếu phương trình có nghiệm $x={{x}_{0}}$ thì đưa (1) thành: $(x-{{x}_{0}})h(x,m)=0$ và tiếp tục biện luận với phương trình $h(x,m)=0$

B/ VÍ DỤ

VD 1: Tìm m để Parabol (P):$y={{x}^{2}}-(2m+5)x+{{m}^{2}}+6m$ cắt đồ thị hàm số $y=\frac{-7x+3{{m}^{2}}+3}{x}$ tại 3 điểm phân biệt có hoành độ dương

A.$m\ne 3\pm \sqrt{5}$

B.$m\ne 3\pm \sqrt{5};m>0$

C.$m\ne 3\pm \sqrt{5};m\ne 0$

D.$m\ne 0$

HD: Phương trình hoành độ giao điểm

${{x}^{2}}-(2m+5)x+{{m}^{2}}+6m=\frac{-7x+3{{m}^{2}}+3}{x}$ $$(*)

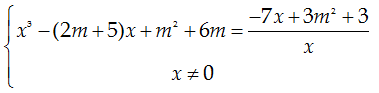
Yêu cầu bài toán ↔ Phương trình (*)trên có 3 nghiệm phan biệt dương khác 0.

$(*)\Leftrightarrow \left( x-3 \right)\left[ {{x}^{2}}-2(m+1)x+{{m}^{2}}+1 \right]=0$

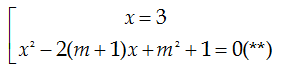
Phương trình (*) có 3 nghiệm phân biệt khi và chỉ khi phương trình (**) có 2 nghiệm phân biệt khác 3

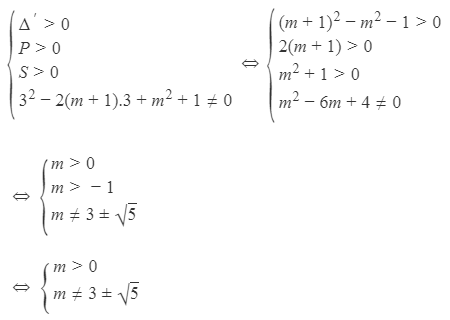
Vậy m>0; $m\ne 3\pm \sqrt{5}$

Đáp án B

VD 2: Cho hàm số $y=(m+1){{x}^{4}}-4{{x}^{2}}+1(C)$ . Tìm m để (C) cắt trục hoành tại ít nhất một điểm

A.$m=3$

B.$m\le 3$

C.$m\ne 3$

D.$m\ge 3$

HD:

Hoành độ gioa điểm của (C) và trục hoành là nghiệm của phương trình:

$(m+1){{x}^{4}}-4{{x}^{2}}+1=0$ (1)

Đặt $t={{x}^{2}},t\ge 0$ phương trình trở thành

$(m+1){{t}^{2}}-4t+1=0$ (2)

Đồ thị (C) cắt trục hoành tại ít nhất một điểm khi phương trình (1) có nghiệm ó phương trình (2) có nghiệm không âm

Với m = -1, phương trình (2) trở thành $-4t+1=0\Leftrightarrow t=\frac{1}{4}>0$ (thõa mãn)

Với $m\ne 1$ ta có 3 trường hợp:

+ TH 1: (2) có 2 nghiệm không âm

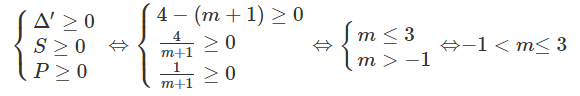
+ TH 2: phương trình (2) có hai nghiệm trái dấu $\Leftrightarrow P<0\Leftrightarrow \frac{1}{m+1}<0\Leftrightarrow m<-1$

+ TH 3: phương trình (2) có một nghiệm bằng 0 và một nghiệm không âm (loại)

Vậy $m\le 3$

Đáp án B

VD 3: Cho hàm số $y=\frac{2x-3}{x-1}$ có đồ thị hàm số (H). Tìm m để đường thẳng (d): x + 3y + m = 0 cắt (H) tại hai điểm M, N sao cho tam giác AMN vuông tại điểm A(1;0)

A.m=-6

B.m=0

C.m=-5

D.m=-3

HD:

Phương trình hoành độ giao điểm của (H) và (d)

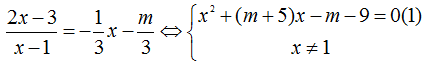
Để (H) vắt d tại hai điểm phân biệt thì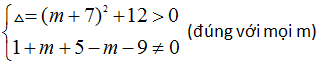

Do đó (d) luôn cắt (H) tại 2 điểm phân biệt $M({{x}_{1}};{{y}_{1}});N({{x}_{2}};{{y}_{2}})$

Ta có $\overrightarrow{AM}=({{x}_{1}}-1;{{y}_{1}});\overrightarrow{AN}({{x}_{2}}-1;{{y}_{2}})$

Tam giác AMN vuông tại A

$\Leftrightarrow \overrightarrow{AM}.\overrightarrow{AN}=0$ hay $({{x}_{1}}-1)({{x}_{2}}-1)+{{y}_{1}}{{y}_{2}}=0$

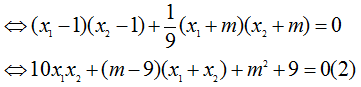
Áp dụng định lý Viet:

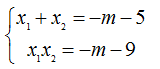
Thay vào (2), ta được

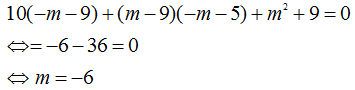
Đáp án A

VD 4: Cho hàm spps $y=\frac{2mx-3-2m}{x+2}$ có đồ thi (C). Xác định m để đường thẳng (d): y = x – 2 cắt (C) tại hai điểm phân biệt A, B sao cho góc giữa hai đường thẳng Oa và OA bằng ${{45}^{0}}$

A.$m=\frac{3}{2}$

B.$m=\frac{1}{2}$

C.$m=\frac{3}{2}\And m=\frac{1}{2}$

D.Không tồn tại m

HD:

Phương trình hoành độ giao điểm

$\frac{2mx-3-2m}{x+2}=x-2\Leftrightarrow (x-1)(x+1-2m)=0$ $(x\ne 2)$ (*)

Đồ thị (C) cắt (d_ tại 2 điểm phân biệt khi (*) có 2 nghiệm phân biệt khác -2

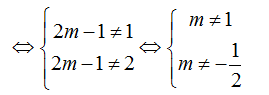
Khi đó tọa độ hai giao điểm là A(1;-1); B(2m-1;2m-3). Để góc giữa OA và OB bằng ${{45}^{0}}$ thì:

$\left| \overrightarrow{OA}.\overrightarrow{OB} \right|=OA.OB.cos{{45}^{0}}$ $$

$1(2m-1)+(-1)(2m-3)=\sqrt{{{1}^{2}}+{{(-1)}^{2}}}.\sqrt{{{(2m-1)}^{2}}+{{(2m-3)}^{2}}}.\frac{1}{\sqrt{2}}$

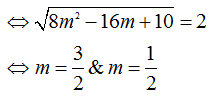
Đáp án C

C/ BÀI TẬP

Bài 1: Cho hàm số $y=(m+1){{x}^{4}}-4{{x}^{2}}+1(C)$ . Tìm m để (C) cắt trục hoành tại 4 điểm phân biệt

A.$-1

B.$-1\le m\le 3$

C.$-1\le m<3$

D.$-1

Bài 2: Cho hàm số $y={{x}^{4}}-3{{x}^{2}}+m$ (C) và $y=-4{{x}^{3}}+14x$ (C’). Tìm m để (C) không cắt (C’)

A.m=0

B.$m>0$

C.$m<0$

D.Không có giá trị m

Bài 3: Cho hàm số $y={{x}^{3}}+2m{{x}^{2}}+3(m-1)x+2$ (1). TÌm m để đồ thị hàm số cắt đường thẳng (d): y = -x + 2 tại 3 điểm phân biệt A(0;2); B; C sao cho tam giác MBC có điện tích $2\sqrt{2}$ với M(3;1)

A.m=0

B.m=3

C.m=0 và m=3

D.m=2

Bài 4: Cho hàm số $y={{x}^{3}}-3(m-2){{x}^{2}}+(m-1)x+4$ (C). Tìm m để (C) cắt đường thẳng (d): x + y – 1 = 0 tại 3 điểm phân biệt có hoành độ lập thành cấp số cộng

A.m=0

B.m=-1

C.m=2

D.m=3

Bài 5: Cho hàm số $y=2{{x}^{3}}+(m-3){{x}^{2}}+(-m+2)x+1$ (C). Tìm m để (C) có hai điểm cực trị A, B sao cho tam giác OAB đều

A.$\frac{1}{\sqrt{15}}$

B.-1

C.$\frac{3}{\sqrt{15}}$

D.$\sqrt{15}$

Câu 6: Tìm m để đồ thị hàm số y = mx cắt đồ thị $y={{x}^{3}}-3{{x}^{2}}$ tại ba điểm phân biệt trong đó có hai điểm có hoành độ dương

A.$m>-\frac{9}{4}$

B.$m\ge -\frac{9}{4}$

C.$m<-\frac{9}{4}$

D.$m\le -\frac{9}{4}$

Câu 7: Trên đồ thị hàm số $y=\frac{x+3}{2x+1}$ có bao nhiêu điểm có tọa độ nguyên?

A.3

B.4

C.2

D.5

Câu 8: Cho hàm số $y=\frac{1}{3}{{x}^{3}}-m{{x}^{2}}-x+m+\frac{2}{3}$ (C). TÌm m để (C) cắt trục Ox tại ba điểm phân biệt có hoành độ thõa mãn $x_{1}^{2}+x_{2}^{2}+x_{3}^{2}>15$

A.m < -1 hoặc m > 1

B.m < -1

C.m > 0

D.m > 1

ĐÁP ÁN