TÍNH LỒI LÕM VÀ ĐIỂM UỐN CỦA ĐỒ THỊ
HÀM SỐ
A/ LÝ THUYẾT
1/ Khái niệm
Cho đồ thị hàm số $y=f(x)$ như hình vẽ, giả sử đồ thị có tiếp tuyến tại mọi điểm
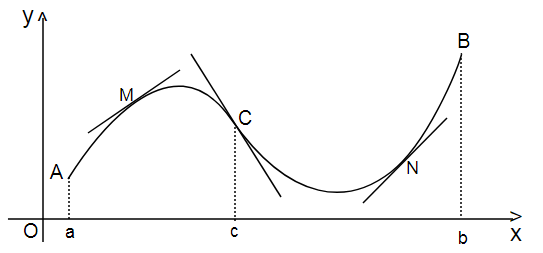
$f''(x)$ <
0 với mọi x thuộc (a;c): hàm số lồi trên (a;c)
$f''(x)$
> 0 với mọi x thuộc (c;b): hàm số lồi lõm trên (c;b)
$f''(x)$ đổi
dấu khi x qua c: hàm số có điểm uốn tại x = c
+ Cung lồi:
AC là một cung lồi khi tại mọi điểm thuộc AC, tiếp tuyến đều nằm trên cung AC.
Khoảng [a;c] là khoảng lồi.
+ Cung lõm: CB
là một cung lồi khi tại mọi điểm thuộc CB, tiếp tuyến đều nằm dưới cung CB. Khoảng
[c;b] là khoảng lõm.
+ Điểm uốn:
điểm chuyển tiếp giữa cung lồi sang cung lõm hoặc ngược lại
2/ Dấu hiệu và cách tìm khoảng lồi,
khoảng lõm và điểm uốn
Định lý: Cho
hàm số $y=f(x)$ có đạo hàm cấp hai trên khoảng (a;b)
+ Nếu $f''(x)<0$
với mọi $x\in \left( a;b \right)$ thì đồ thị hàm số lồi trên khoảng đó
+ Nếu $f''(x)>0$
với mọi $x\in \left( a;b \right)$ thì đồ thị hàm số lõm trên khoảng đó
+ Nếu $f''(x)$
đổi dấu khi đi qua ${{x}_{0}}$ thì điểm ${{M}_{0}}({{x}_{0}};f({{x}_{0}}))$ là
điểm uốn của đồ thị hàm số
B/ VÍ DỤ
VD 1: Khoảng lồi, lõm, và điểm uốn của đồ
thị hàm số $y={{x}^{5}}$ lần lượt là
A.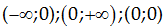
B.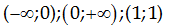
C.$(0;+\infty
);\left( -\infty ;0 \right);(0;0)$
D.$(0;+\infty
);\left( -\infty ;0 \right);(1;1)$
HD:
D= R
$y'=5{{x}^{4}};y''=20{{x}^{3}}$ , ta có bảng xét dấu y’’
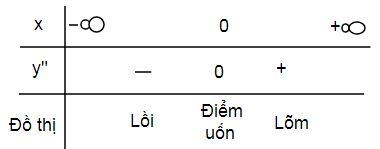
Vậy đồ thị hầm
số lồi trên $\left( -\infty ;0 \right)$ , lõm trên khoảng $\left(
0;+\infty \right)$ và điểm (0;0) là điểm
uốn
Đáp án A
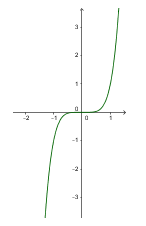
VD 2: Khoảng lồi, lõm, và điểm uốn của đồ
thị hàm số $y=-\sin x$trên đoạn $\left[ 0;2\pi
\right]$ lần lượt là
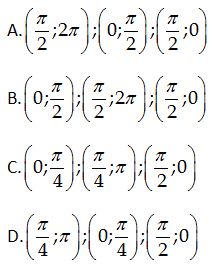
HD:
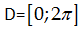
$y'=-\cos
x;y''=\sin x$ , ta có bảng xét dấu y’ trên 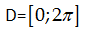
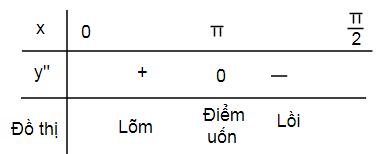
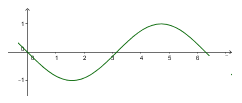
Vậy hàm số $y=-\sin
x$ lõm trên $\left( 0;\frac{\pi }{2} \right)$ , lồi trên $\left( \frac{\pi
}{2};2\pi \right)$ và điểm $\left(
\frac{\pi }{2};0 \right)$ là điểm uốn của
đồ thị
Đáp án B
VD 3: Khoảng lồi, lõm, và điểm uốn của đồ
thị hàm số $y=\frac{x+1}{x-1}$ lần lượt là
A.$\left(
-\infty ;0 \right);(0;+\infty );(0;-1)$
B.$\left(
-\infty ;0 \right);(0;+\infty );\varnothing $
C.$\left(
-\infty ;1 \right);(1;+\infty );\varnothing $
D.$\left(
-\infty ;1 \right);(1;+\infty );(0;-1)$
HD:
$D=(-\infty
;1)\cup (1;+\infty )$
$y'=-\frac{2}{{{(x-1)}^{2}}};y''=\frac{4}{{{(x-1)}^{3}}}$ . Ta có bảng xét dấu dấu của y’’:
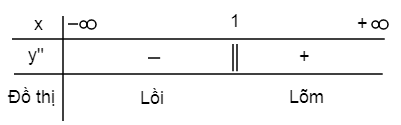
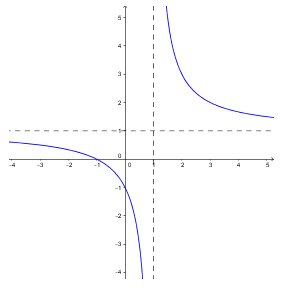
Đồ thị hàm số
lồi trên $\left( -\infty ;1 \right)$ và lõm trên $\left( 1;+\infty \right)$ và không có điểm uốn
Đáp án C
VD 4: Đồ thị hàm số $y=\frac{{{x}^{2}}+3x+2}{{{x}^{2}}+x+1}$
có 3 điểm uốn. Tọa độ 3 điểm uốn này là
A.$\left(
\frac{1}{2};\frac{1}{3} \right),\left( 1;-2 \right),\left( 2;0 \right)$
B.$\left(
-\frac{1}{2};\frac{1}{3} \right),\left( -1;-2 \right),\left( -2;1 \right)$
C.$\left(
-\frac{1}{2};-\frac{1}{3} \right),\left( 1;2 \right),\left( -2;0 \right)$
D.$\left(
\frac{1}{2};-\frac{1}{3} \right),\left( -1;-2 \right),\left( 2;1 \right)$
HD:
$y'=\frac{-2{{x}^{2}}-2x+1}{{{({{x}^{2}}+x+1)}^{2}}}$
$y''=\frac{{{({{x}^{2}}+x+1)}^{2}}(-4x-2)+(2{{x}^{2}}+2x-1)2({{x}^{2}}+x+1)(2x+1)}{{{({{x}^{2}}+x+1)}^{4}}}$
$=\frac{(2x+1)({{x}^{2}}+x+1)(-2{{x}^{2}}-2x-2+4{{x}^{2}}+4x-2)}{{{({{x}^{2}}+x+1)}^{4}}}$
$=\frac{(2x+1)(2{{x}^{2}}+2x-4)}{{{({{x}^{2}}+x+1)}^{3}}}$
$y''=0\Leftrightarrow
(2x+1)(2{{x}^{2}}+2x-4)=0$
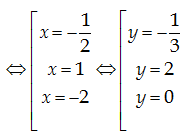
Đáp án C
C/ BÀI TẬP TỰ LUYỆN
Câu 1: Cho hàm số $y=2{{x}^{2}}+16\operatorname{cosx}-\cos
2x$ . Hoành độ các điểm uốn của đồ thị hàm số này là
A.$x=\frac{\pi
}{4}+k\frac{\pi }{2}$
B.$x=\frac{\pi
}{2}+k2\pi $
C.$x=\frac{\pi
}{2}+k\pi $
D.$x=\frac{3\pi
}{2}+k2\pi $
Câu 2: Giá trị của m để đồ thị hàm số $y={{x}^{3}}+3m{{x}^{2}}+(m+2)x-m+2$
có điểm uốn nằm trên trục hoành là
A.$1;\frac{-1-\sqrt{17}}{4};\frac{-1+\sqrt{17}}{4}$
B.$-1;\frac{1+\sqrt{17}}{4};\frac{1-\sqrt{17}}{4}$
C.$1;-\frac{3}{4};\frac{5}{4}$
D.$-1;\frac{3}{4};-\frac{5}{4}$
Câu 3: Cho hàm số $y=a{{x}^{3}}+b{{x}^{2}}+x+1$
. Để điểm I(1;-2) là điểm uốn của đò thị hàm số, các giá trị của a, b lần lượt
là
A.-2;6
B.2;-6
C.-2;-6
D.2;6
Câu 4: Đồ thị của hàm số $y=\frac{{{(x+1)}^{3}}}{{{x}^{2}}-x+1}$
có 3 điểm uốn. Tọa độ của các điểm uốn này là
A.$\left(
-1;0 \right),\left( 2;9 \right),\left( \frac{1}{2};\frac{9}{2} \right)$
B.$\left(
1;2 \right),\left( 2;-9 \right),\left( \frac{1}{2};-\frac{9}{2} \right)$
C.$\left(
0;1 \right),\left( -2;-9 \right),\left( -\frac{1}{2};-\frac{9}{2} \right)$
D.$\left(
-2;1 \right),\left( 1;-2 \right),\left( -\frac{1}{2};\frac{9}{2} \right)$
Câu 5: Đường thẳng đi qua 3 điểm uốn của đồ
thị hàm số $y=\frac{x-1}{{{x}^{2}}+1}$ đều nằm trên một đường thẳng. Đường thẳng
này có phương trình là
A.x + 4y – 3
= 0
B.x – 4y – 3
= 0
C.x + 4y + 3
= 0
D.x – 4y + 3
= 0
Câu 6: Đường thẳng đi qua 3 điểm uốn của đồ
thị hàm số $y=\frac{2x+1}{{{x}^{2}}+x+1}$ đều nằm trên một đường thẳng. Đường
thẳng này có phương trình là
A.2x – 3y +
1 = 0
B.2x – 3y –
1 = 0
C.2x + 3y +
1 =0
D.2x + 3y –
1 =0
Câu 7: Cho hàm số $y={{x}^{3}}-3m{{x}^{2}}+(m+2)x+2m+3$
. Để điểm uốn của đồ thị hàm số nằm trên parabol $y=2{{x}^{2}}$ , giá trị thích
hợp của m là
A.$m=1;m=-\frac{3}{2}$
B.$m=-1;m=\frac{3}{2}$
C.$m=1;m=-3$
D.$m=3;m=-1$
Câu 8: Cho hàm số $y=a{{x}^{3}}+b{{x}^{2}}$
. Để đồ thị của hàm số nhận điểm
I(-1;-2) là điểm uốn thì giác trị của a, b lần lượt là
A.1;3
B.-1;-3
C.-3;1
D.3;-1
Câu 9: Cho hàm số $y=a{{x}^{3}}+b{{x}^{2}}+x+1$
. Để điểm I(1;-2) là điểm uốn của đò thị hàm số, các giá trị của a, b lần lượt
là
A.-2;6
B.2;-6
C.-2;-6
D.2;6
Câu 10: Cho hàm số $y={{x}^{4}}+2b{{x}^{2}}+4$
có đồ thị là (C). Để (C) không có điểm uốn, giá trị của b là
A.b > 0
B.b < 0
C.Không tồn
tại giá trị của b
D.Tất cả đều
sai
ĐÁP ÁN
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
C |
A |
B |
A |
B |
A |
B |
B |
B |
A |







