- Lý thuyết
- Với a, b \[\in \] N, b ≠ 0 thì ta có a/b gọi là phân số. Trong đó a là tử số, b là mẫu số của phân số.
- Phân số Ai cập là phân số có dạng 1/n (có tử bằng 1)
- Mọi số tự nhiên đều có thể viết dưới dạng phân số, VD: 8 = 8/1 = 16/2 = ……
* Muốn viết 1 số tự nhiên dưới dạng phân số có mẫu số là 1 ta viết tử số bằng số tự nhiên đó, còn mẫu số là 1. VD 9 = 9/1 . TQ A = A/1
* Muốn viết 1 số tự nhiên dưới dạng 1 phân số có mẫu số là số cho trước ta viết mẫu số bằng số cho trước, còn tử số bằng tích của số tự nhiên với mẫu số cho trước.
VD 4 = x/3, ta có phân số: 4.3/3 = 12/3
TQ: A = x/B = A.B/B
- Phân số thập phân là phân số có mẫu là 10, 100, 1000,…….
- Các phân số bằng nhau được coi là cùng 1 giá trị, giá trị đó là số biểu diễn bởi phân số. Tập hợp các số biểu diễn bởi phân số kí hiệu là Q+ . VD : 2/3 = 4/6 = 6/9 = ……..
TQ: a/b = c/d ó a.d = b.c
* Tính chất: (1) Phản xạ: a/b = b/a
(2) Đối xứng: Nếu a/b = c/d thì c/d = a/b
(3) Bắc cầu: Nếu a/b = c/d và c/d = e/f thì a/b = e/f
II . Bài tập
Bài 1: Định nghĩa hai phân số bằng nhau. Cho VD?
Bài 2: Dùng 2 trong 3 số sau 2, 3, 5 để viết thành phân số (tử số và mẫu số khác nhau)
Hướng dẫn Có các phân số: \[\frac{2}{3};\frac{2}{5};\frac{3}{5};\frac{3}{2}\frac{5}{2};\frac{5}{3}\]
Bài 3: 1/ Số nguyên a phải có điều kiện gì để ta có phân số?
a/ \[\frac{32}{a-1}\] b/ \[\frac{a}{5a+30}\]
2/ Số nguyên a phải có điều kiện gì để các phân số sau là số nguyên:
a/ \[\frac{a+1}{3}\] b/ \[\frac{a-2}{5}\]
3/ Tìm số nguyên x để các phân số sau là số nguyên:
a/ \[\frac{13}{x-1}\] b/ \[\frac{x+3}{x-2}\]
Hướng dẫn
1/ a/ \[a\ne 0\] b/ \[a\ne -6\]
2/ a/ \[\frac{a+1}{3}\] \[\in \] Z khi và chỉ khi a + 1 = 3k (k \[\in \] Z). Vậy a = 3k – 1 (k \[\in \] Z)
b/ \[\frac{a-2}{5}\] \[\in \] Z khi và chỉ khi a - 2 = 5k (k \[\in \] Z). Vậy a = 5k +2 (k \[\in \] Z)
3/ \[\frac{13}{x-1}\]\[\in \] Z khi và chỉ khi x – 1 là ước của 13.
Các ước của 13 là 1; -1; 13; -13
|
x - 1 |
-1 |
1 |
-13 |
13 |
|
x |
0 |
2 |
-12 |
14 |
Suy ra:
b/ \[\frac{x+3}{x-2}\] = \[\frac{x-2+5}{x-2}=\frac{x-2}{x-2}+\frac{5}{x-2}=1+\frac{5}{x-2}\]\[\in \] Z khi và chỉ khi x – 2 là ước của 5.
|
x - 2 |
-1 |
1 |
-5 |
5 |
|
x |
1 |
3 |
-3 |
7 |
Bài 4: Tìm x biết:
a/ \[\frac{x}{5}=\frac{2}{5}\] b/ \[\frac{3}{8}=\frac{6}{x}\] c/ \[\frac{1}{9}=\frac{x}{27}\] d/ \[\frac{4}{x}=\frac{8}{6}\] e/ \[\frac{3}{x-5}=\frac{-4}{x+2}\] f/ \[\frac{x}{-2}=\frac{-8}{x}\]
Hướng dẫn
a/ \[\frac{x}{5}=\frac{2}{5}\]\[\Rightarrow x=\frac{5.2}{5}=2\] b/ \[\frac{3}{8}=\frac{6}{x}\]\[\Rightarrow x=\frac{8.6}{3}=16\] c/ \[\frac{1}{9}=\frac{x}{27}\]\[\Rightarrow x=\frac{27.1}{9}=3\]
d/ \[\frac{4}{x}=\frac{8}{6}\]\[\Rightarrow x=\frac{6.4}{8}=3\]
e/ \[\frac{3}{x-5}=\frac{-4}{x+2}\]
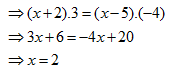
f/ \[\frac{x}{-2}=\frac{-8}{x}\]
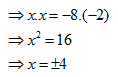
Bài 5: 1/ Chứng minh rằng \[\frac{a}{b}=\frac{c}{d}\] thì \[\frac{a}{b}=\frac{a\pm c}{b\pm d}\]
2/ Tìm x và y biết \[\frac{x}{5}=\frac{y}{3}\] và x + y = 16
Hướng dẫn
a/ Ta có \[\frac{a}{b}=\frac{c}{d}\Rightarrow ad=bc\Rightarrow ad\pm ab=bc\pm ab\Rightarrow a(b\pm d)=b(a\pm c)\] Suy ra: \[\frac{a}{b}=\frac{a\pm c}{b\pm d}\]
b/ Ta có: \[\frac{x}{5}=\frac{y}{3}=\frac{x+y}{8}=\frac{16}{8}=2\] Suy ra x = 10, y = 6
Bài 6: Cho \[\frac{a}{b}=\frac{c}{d}\], chứng minh rằng \[\frac{2a-3c}{2b-3d}=\frac{2a+3c}{2a+3d}\]
Hướng dẫn
Áp dụng kết quả chứng minh trên ta có \[\frac{a}{b}=\frac{c}{d}=\frac{2a-3c}{2b-3d}=\frac{2a+3c}{2b+3d}\]
Bài 7: Một người đi xe đạp với vận tốc a km/h. Hỏi trong 30 phút người ấy đi được bao nhiêu km? Trong 1 phút người ấy đi được bao nhiêu km? (ĐS: a/2 km; a/60 km)
Bài 8: Sau a giờ, kim giờ quay được bao nhiêu vòng? (ĐS: a/12 vòng)
Bài 9: Một ngọn nến cháy từ 7h12/ à 7h25/ . Hỏi thời gian nến cháy là mấy phần của 1h?
Bài 10: Một người lien lạc phải đi 1 con đường dài 132km. Mỗi ngày đi được 35 km. Hỏi sau 3 ngày người ấy đi được mấy phần đường?
Bài 11: Một vòi nước chảy vào một cái bể từ 10h đêm à 6h sáng hôm sau. Mỗi giờ vòi chảy vào bể được 360 lít nước. Bể có thể chứa được 4m3 và lúc đầu đã chứa 1100 lít. Hỏi đến 6h sang thì khối nước trong bể chiếm mấy phần bể?
Bài 12: Tìm số tự nhiên x biết rằng a) Phân số x/15 có giá trị = 3
b) Phân số 132/x có giá trị = 11
Bài 13: Tìm 1 phân số biết rằng a) 1/3 = 1/4 số đó (ĐS: 4/3)
b) 1/4 = 1/3 số đó (ĐS: 3/4)
Bài 14: Viết số 100 dưới dạng tổng của 1 số tự nhiên và 1 phân số bằng cách dung:
a) 6 chữ số giống nhau b) 9 chữ số khác nhau
Hướng dẫn
a) 100 = 99 + 99/99
b) Có nhiều đáp số. Ví dụ: 100 = 91 + 5742/638 = 92 + 5104/638 = 93 + 1456/208 =
94 + 1578/263 = 95 + 1380/276 = 97 + 1602/534 = 98 + 1072/536 = …v.v..
Bài 15: Dùng 9 chữ số khác nhau và khác 0 để viết các phân số có giá trị lần lượt bằng 2, 3, 4, 5, 6, 7, 8, 9.
Hướng dẫn
Có nhiều cách viết: 15846/7923 = 2 ; 17496/5832 = 3 ; 15768/4392 = 4
31485/6297 = 5 ; 34182/5697 =6 ; 31689/4527 = 7 ; 47328/5916 = 8 ; 57249/8361 = 9
Bài 16: CMR các phân số sau bằng nhau:
a/ 23/99 = 2323/9999 = 232323/999999 b/ 29/43 = 2929/4343
c/131313/151515 = 13026/15030 d/ (27425 – 27)/99900 = (27425425 - 27425)/99900000
e/ (29700 – 54)/(30800 - 56) = (59400 – 108)/(61600 - 112)
f) 9909/8808 = 29727/26424 = 39636/35232
Hướng dẫn
a/ * 2323/9999 = 23.101/99.101 = 23/29 * 232323/999999 = 23.10101/99.10101 = 23/99
d/ * (27425425 - 27425)/99900000 = (27425000 + 425 - 27000 - 425)/99900000 =
[(27425 - 27).1000]/99900. 1000 = (27425 – 27)/99900
e/ (29700 – 54)/(30800 - 56) = [(29700 – 54).2]/[(30800 – 56).2] = (59400 – 108)/(61600 - 112)
f/ 9909/8808 = 9909.3/8808.3 = 29727/26424 = 39636/35232
Bài 17: Điền số thích hợp:
a/ 4/5 = ?/60 b/ ?/9 = 12/54 c/ 63/72 = 7/? d/ 65/? = 5/9
Bài 18: Tìm phân số bằng phân số 13/17 biết rằng tổng của tử và mẫu của nó bằng 900?
Bài 19: Tìm phân số bằng phân số 188887/211109 biết rằng tổng của tử và mẫu của nó bằng 108?
Bài 20: Tìm x, y biết rằng: (3 + x)/(5 + y) = 3/5 và x + y = 16
Bài 21: CMR nếu 3 phân số a/b; c/d ; e/f bằng nhau thì phân số (a.m + c.n + e.f)/(b.m + d.n + f.p)
(m, n, p là các số tự nhiên khác 0) cũng bằng các phân số đã cho.







