B. TÍNH CHẤT CƠ BẢN CỦA PHÂN SỐ - RÚT GỌN PHÂN SỐ
- Lý thuyết
1. Tính chất
- Nếu nhân cả tử số và mẫu số của 1 phân số với cùng 1 số tự nhiên, hoặc 1 số nguyên khác 0 thì ta được 1 phân số bằng phân số đã cho. TQ: a/b = a.m/b.m ( m \[\in \] N hoặc m \[\in \] Z, m ≠ 0)
- Nếu chia cả tử số và mẫu số của 1 phân số với cùng 1 số tự nhiên, hoặc 1 số nguyên khác 0 thì ta được 1 phân số bằng phân số đã cho. TQ: a/b = a:m/b:m ( m \[\in \] N hoặc m \[\in \] Z, m ≠ 0)
2. Rút gọn phân số
- Là chia tử và mẫu của chúng cho 1 số (ước chung) khác ±1 của chúng để được 1 phân số đơn giản hơn và bằng phân số đã cho.
- Một phân số không thể rút gọn được nữa gọi là phân số tối giảnTQ:a/b tối giản óƯCLN(a,b)= 1
(a và b nguyên tố cùng nhau)
3. Phương pháp rút gọn phân số
- Rút gọn từng bước dựa vào dấu hiệu chia hết. VD 30/105 = 30: 5/ 105: 5 = 2/7
- Chia tử và mẫu cho ƯCLN của chúng để rút gọn hoàn toàn. VD ƯCLN(30,105) = 15
=> 30: 15/ 105: 15 = 2/7
II. Bài tập
Bài 1: 1/ Chứng tỏ rằng các phân số sau đây bằng nhau:
a/ \[\frac{25}{53}\] ; \[\frac{2525}{5353}\] và \[\frac{252525}{535353}\] b/ \[\frac{37}{41}\] ; \[\frac{3737}{4141}\] và \[\frac{373737}{414141}\]
2/ Tìm phân số bằng phân số \[\frac{11}{13}\] và biết rằng hiệu của mẫu và tử của nó bằng 6.
Hướng dẫn
1/ a/ Ta có:
* \[\frac{2525}{5353}\] = \[\frac{25.101}{53.101}=\frac{25}{53}\] * \[\frac{252525}{535353}\] = \[\frac{25.10101}{53.10101}=\frac{25}{53}\]
b/ Tương tự
2/ Gọi phân số cần tìm có dạng \[\frac{x}{x+6}\](x\[\ne \]-6), theo đề bài thì \[\frac{x}{x+6}\]=\[\frac{11}{13}\]
Từ đó suy ra x = 33, phân số cần tìm là \[\frac{33}{39}\]
Bài 2: Điền số thích hợp vào ô vuông
a/ \[\frac{1}{2}=\frac{}{}\] b/ \[\frac{5}{-7}=\frac{}{}=\frac{}{}\]
Hướng dẫn
a/ \[\frac{1}{2}=\frac{}{}=\frac{3}{6}=\frac{4}{8}=...\] b/ \[\frac{5}{-7}=\frac{}{}=\frac{}{}=\frac{-20}{28}=\cdot \cdot \cdot \]
Bài 3. Giải thích vì sao các phân số sau bằng nhau:
a/ \[\frac{-22}{55}=\frac{-26}{65}\]; b/ \[\frac{114}{122}=\frac{5757}{6161}\]
Hướng dẫn
a/ * \[\frac{-22}{55}=\frac{-21:11}{55:11}=\frac{-2}{5}\]; * \[\frac{-26}{65}=\frac{13}{65:13}=\frac{-2}{5}\]
b/ HS giải tương tự
Bài 4. Rút gọn các phân số sau: \[\frac{125}{1000};\frac{198}{126};\frac{3}{243};\frac{103}{3090}\]
Hướng dẫn
\[\frac{125}{1000}=\frac{1}{8};\frac{198}{126}=\frac{11}{7};\frac{3}{243}=\frac{1}{81};\frac{103}{3090}=\frac{1}{30}\]
Rút gọn các phân số sau: a/ \[\frac{{{2}^{3}}{{.3}^{4}}}{{{2}^{2}}{{.3}^{2}}.5};\frac{{{2}^{4}}{{.5}^{2}}{{.11}^{2}}.7}{{{2}^{3}}{{.5}^{3}}{{.7}^{2}}.11}\] b/ \[\frac{121.75.130.169}{39.60.11.198}\] c/ \[\frac{1998.1990+3978}{1992.1991-3984}\]
Hướng dẫn
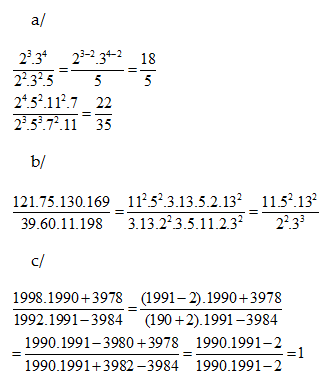
Bài 5. Rút gọn
a/ \[\frac{{{3}^{10}}.{{(-5)}^{21}}}{{{(-5)}^{20}}{{.3}^{12}}}\] b/ \[\frac{-{{11}^{5}}{{.13}^{7}}}{{{11}^{5}}{{.13}^{8}}}\] c/ \[\frac{{{2}^{10}}{{.3}^{10}}-{{2}^{10}}{{.3}^{9}}}{{{2}^{9}}{{.3}^{10}}}\] d/ \[\frac{{{5}^{11}}{{.7}^{12}}+{{5}^{11}}{{.7}^{11}}}{{{5}^{12}}{{.7}^{12}}+{{9.5}^{11}}.7{}^{11}}\]
Hướng dẫn
a/ \[\frac{{{3}^{10}}.{{(-5)}^{21}}}{{{(-5)}^{20}}{{.3}^{12}}}=\frac{-5}{9}\] c/ \[\frac{{{2}^{10}}{{.3}^{10}}-{{2}^{10}}{{.3}^{9}}}{{{2}^{9}}{{.3}^{10}}}=\frac{4}{3}\]
Bài 6. Tổng của tử và mẫu của phân số bằng 4812. Sau khi rút gọn phân số đó ta được phân số \[\frac{5}{7}\]. Hãy tìm phân số chưa rút gọn.
Hướng dẫn
Tổng số phần bằng nhau là 12
Tổng của tử và mẫu bằng 4812
Do đó: tử số bằng 4811:12.5 = 2005
Mẫu số bằng 4812:12.7 = 2807.
Vậy phân số cần tìm là \[\frac{2005}{2807}\]
Bài 7. Mẫu số của một phân số lớn hơn tử số 14 đơn vị. Sau khi rút gọn phân số đó ta được \[\frac{993}{1000}\]. Hãy tìm phân số ban đầu.
Hướng dẫn
Hiệu số phần của mẫu và tử là 1000 – 993 = 7
Do đó tử số là (14:7).993 = 1986
Mẫu số là (14:7).1000 = 2000
Vạy phân số ban đầu là \[\frac{1986}{2000}\]
Bài 8: a/ Với a là số nguyên nào thì phân số \[\frac{a}{74}\] là tối giản.
b/ Với b là số nguyên nào thì phân số \[\frac{b}{225}\] là tối giản.
c/ Chứng tỏ rằng \[\frac{3n}{3n+1}(n\in N)\]là phân số tối giản
Hướng dẫn
a/ Ta có \[\frac{a}{74}=\frac{a}{37.2}\] là phân số tối giản khi a là số nguyên khác 2 và 37
b/ \[\frac{b}{225}=\frac{b}{{{3}^{2}}{{.5}^{2}}}\] là phân số tối giản khi b là số nguyên khác 3 và 5
c/ Ta có ƯCLN(3n + 1; 3n) = ƯCLN(3n + 1 – 3n; 3n) = ƯCLN(1; 3n) = 1
Vậy \[\frac{3n}{3n+1}(n\in N)\]là phân số tối giản (vì tử và mẫu là hai số nguyên tố cùng nhau)
Bài 9: Rút gọn các phân số sau:
a/ 103/3090 ; 7314/18126 ; 68952/148512 ; 121.75.130.169/39.60.11.198
b/ 9/(33 – 6) ; 17.(1993 – 45)/(1993 – 45). (52 – 18) ; 7/( 102 + 6. 102 )
Bài 10: Rút gọn các phân số sau:
a/ A = (31995 – 81)/(42660 – 108) => A = 81.(395 – 1)/108.(395 – 1) = 3/4
b/ B = (3.5.7.11.13.37 - 10101)/(1212120 - 41414)
=> B = (5.11.10101 - 10101)/(10101.120 + 10101.4) = 10101.(5.11 - 1)/10101.(120 + 4) = 54/124 = 27/62
Bài 11: Phân số (5n + 6)/(8n + 7) (n \[\in \] N ) có thể rút gọn cho phân số nào?
Hướng dẫn
G.S (5n + 6)/(8n + 7) rút gọn được cho k (k \[\in \] N, k > 1 ). Tức (5n + 6) và (8n + 7) cùng chia hết cho k. Do dó: 8.(5n + 6) – 5.(8n + 7) ℅ k Hay 13 ℅ k. Vì k > 1 => k = 13
Bài 12: Tìm mọi số tự nhiên n để phân số (18n + 3)/(21n + 7) có thể rút gọn được?
Hướng dẫn
-
- (18n + 3)/(21n + 7) = 3.(6n + 1)/7.(3n + 1)
- Nhận thấy: 3 và 7, 3 và (3n + 1), (6n + 1) và (3n + 1) đều là cá số nguyên tố cùng nhau.
- Do đó: nếu (6n + 1) ℅ 7 thì phân số (18n + 3)/(21n + 7) có thể rút gọn được.
- Vì 7n ℅ 7 nên nếu (6n + 1) ℅ 7 thì 7n – (6n + 1) = (n – 1) ℅ 7
- => nếu n = 7k + 1 (k \[\in \] N) thì phân số (18n + 3)/(21n + 7) có thể rút gọn được.
- Ví dụ: k = 0, n = 1 ta có: (18n + 3)/(21n + 7) = 3/4
k = 1, n = 8 ta có: (18n + 3)/(21n + 7) = 21/25
Bài 13: Cho phân số: x/y có (x + y) = 316293 và (y – x) = 51015.
a/ Hãy xác định phân số đó rồi rút gọn
b/ Nếu thêm 52 vào tử của phân số trên trước khi đã tối giản thì phải thêm vào mẫu bao nhiêu để giá trị của phân số không đổi?
Hướng dẫn
a/ 132639/183654 = 13. (10000 + 200 + 3)/18. (10000 + 200 + 3) = 13/18
b/ Thêm 72 vào
Bài 14: CMR Phân số sau tối giản a/ (12n + 1)/(30n + 2) b/ (21n + 4)/(14n + 3) (n \[\in \] N)
Hướng dẫn
a/ Gọi d là ước chung của (12n + 1) và (30n + 2) . Ta có 5.(12n + 1) – 2.(30n + 2) = 1 ℅ d
Vậy d = 1 nên (12n + 1) và (30n + 2) nguyên tố cùng nhau.
b/ Tương tự câu a
Bài 15: Cho phân số (n + 9)/(n – 6) (n > 6, n \[\in \] N)
a/ Tìm mọi giá trị của n để phân số có giá trị là số tự nhiên?
b/ Tìm mọi giá trị của n để phân số là số tối giản?
Hướng dẫn
a/ phân số (n + 9)/(n – 6) có giá trị là số tự nhiên khi (n + 9) ℅ (n – 6) hay 15 ℅ (n – 6)
(n – 6) = 1 à n = 7
(n – 6) = 3 à n = 9
(n – 6) = 5 à n = 11
(n – 6) = 15 àn = 21
Vậy khi n \[\in \] (7, 9, 11, 21) thì phân số (n + 9)/(n – 6) có giá trị là số tự nhiên.
b/ (n + 9; n – 6) = (n- 6; 15). Vậy muốn (n + 9; n – 6) = 1 để phân số đã cho là tối giản thì phải có (n- 6; 15) = 1 => (n – 6) ℅ 3 và (n – 6) ℅ 5. Do đó n ≠ 3k và n ≠ (5k + 1)
Bài 16: Tìm số tự nhiên n nhỏ nhất để các phân số sau đây là tối giản: 7/(n + 9) ; 8/(n + 10) ; 9/(n + 11) ; ……..; 31/(n + 33)
Hướng dẫn
Các phân số đã cho có dạng a/a + (n + 2). Vì các phân số này tối giản nên (a + 2) và a phải nguyên tố cùng nhau. Vậy (n + 2) phải nguyên tố cùng nhau với 7, 8, 9, …. , 31 và (n +2) là số nhỏ nhất. Vậy (n + 2) phải là số nguyên tố nhỏ nhất lớn hơn 31, tức là (n +2) =37 à n = 35
Bài 17:Tìm các phân số theo thứ tự bằng các phân số 6/10, 44/77, 30/55 sao cho mẫu của phân số thứ nhất bằng tử của phân số thứ hai, mẫu của phân số thứ hai bằng tử của phân số thứ ba?
Hướng dẫn
* Rút gọn các phân số đã cho: 6/10 = 3/5 ; 44/77 = 4/7 ; 30/55 = 6/11
Vì 3/5 ; 4/7 ; 6/11 là tối giản nên các phân số phải tìm có dạng : 3m/5m ; 4n/7n ; 6p/11p
(m, n, p \[\in \] N* )
Theo đề bài ta có: 5m = 4n và 7n = 6p => 4n ℅ 5 và 7n ℅ 6 và do (4,5) = 1, (7, 6) =1
Nên n ℅ 5 và n ℅ 6. Vậy n ℅ 30.
Đặt n = 30k (k \[\in \] N* ), ta có m = 4n/5 = 4.30k/5 = 24k ; p = 7n/6 = 7.30k/6 =35
Vậy các phân số phải tìm là: 3m/5m = 3.24k/5.24k = 72k/120k
4n/7n = 4.30k/7.30k = 120k/210k
6p/11p = 6.35k/11.35k = 210k/385k







