Căn bậc hai của số phức và phương trình bậc hai
A. Lý thuyết
I. Căn bậc hai của số phức
- Định nghĩa: Cho số phức w. Mỗi số phức z thỏa mãn ${{z}^{2}}=\text{w}$ được gọi là căn bậc hai của w.
- Chú ý: Số 0 có đúng 1 căn bậc hai là 0.
Mỗi số phức khác 0 có hai căn bậc hai là hai số đối nhau (khác 0).
Đặc biệt, số thực a dương có hai căn bậc hai là $\sqrt{a}$ và -$\sqrt{a}$
Số thực a âm có hai căn bậc hai là $\sqrt{-a}i$ và -$\sqrt{-a}i$.
II. Phương trình bậc hai
- Nhờ tính được căn bậc hai của số phức, phương trình $A{{z}^{2}}+Bz+C=0$ (1) đều có nghiệm phức.
- Xét biệt thức $\Delta ={{B}^{2}}-4AC$.
- Nếu $\Delta >0$ thì phương trình (1) có hai nghiệm phân biệt: ${{z}_{1}}=\frac{-B+\delta }{2A};{{z}_{2}}=\frac{-B-\delta }{2A}$. Trong đó, $\delta $ là một căn bậc hai của $\Delta $.
- Nếu $\Delta =0$ thì phương trình (1) có nghiệm kép: ${{z}_{1}}={{z}_{2}}=\frac{-B}{2A}$.
- Chú ý: Định lý vi-et vẫn đúng đối với phương trình bậc hai trong tập số phức
.png)
Người ta chứng minh được rằng mọi phương trình bậc n ${{A}_{0}}{{z}^{n}}+{{A}_{1}}{{z}^{n-1}}+...+{{A}_{n}}=0$ luôn có n nghiệm phức (không nhất thiết phân biệt).
III. Các phương pháp tính căn bậc hai của số phức
1. Tự luận
- Cho số phức w=a+bi. Tìm căn bậc hai số phức w
z=x+yi là căn bậc hai của số phức w \[\Leftrightarrow {{z}^{2}}=\text{w}\]\[\Leftrightarrow {{\left( x+yi \right)}^{2}}=a+bi\]\[\Leftrightarrow {{x}^{2}}-{{y}^{2}}+2xyi=a+bi\]\[\Leftrightarrow \] .png)
.
- Vậy để tìm căn bậc hai của w=a+bi ta cần giải hệ phương trình trên. Mỗi cặp nghiệm (x;y) tương ứng với một căn bậc hai của số phức w.
2. Sử dụng VINACAL (các loại máy khác bấm tương tự)
- Lưu ý: Trước khi làm, các bạn hãy chuyển sang chế độ tính góc bằng Radian.
Cách 1: Ta sử dụng chức năng phím trong chế độ tính toán thường (MODE 1)
.png)
\[\left( SHIFT\to + \right)\]: Chuyển từ dạng tọa độ cực sang dạng lượng giác..png)
\[\left( SHIFT\to - \right)\]: Chuyển từ dạng lượng giác sang tọa độ cực.- Ví dụ: Muốn tìm căn bậc hai số phức z=8+6i. Ta nhập lần lượt vào máy như sau:
.png)
.png)
.png)
.png)
.png)
- Như các bạn thấy trong hai hình cuối chính là kết quả của căn bậc hai của số phức z=8+6i là w=3+i và w=-3-i.
- Chú ý: Cách trên cũng giúp ta tìm được căn bậc n của một số phức bất kì.
Cách 2: Ta chuyển sang chế độ số phức (CMPLEX)(MODE 2)
- Các phím chức năng sử dụng trong chế độ số phức ở SHIFT 2 .
- Ví dụ như trên, các bạn nhập như sau:
.png)
.png)
.png)
.png)
.png)
.png)
- Chú ý: Cách trên cũng giúp ta tìm được căn bậc n của một số phức bất kì.
- Như vậy: Qua 3 cách trên, ta thấy được sự giúp ích của máy tính. Tuy nhiên, để các bạn hiểu rõ hơn về cả ba cách, mỗi bài tập minh họa mình sẽ dùng 1 cách. Các bạn có thể làm theo 2 cách còn lại để rèn luyện.
B. Bài tập
I. Bài tập minh họa
|
Câu 1: Tìm các căn bậc hai của số phức z=-3+4i. A. 1+2i; -1+2i B. 2+2i; -1-2i C. 1+2i; -1-2i D. -2-I; -2+i
|
Lời giải: Chọn C
Cách 1: Thử trực tiếp từng đáp án. Ta thấy ${{\left( 1+2i \right)}^{2}}={{\left( -1-2i \right)}^{2}}=-3+4i$.
Cách 2: Dùng tự luận: ${{\left( x+yi \right)}^{2}}=-3+4i\Leftrightarrow {{x}^{2}}-{{y}^{2}}+2xyi=-3+4i\Leftrightarrow $.png)
.png)
$\Leftrightarrow $.png)
$\Leftrightarrow $.png)
.Nên C là đáp án đúng.
|
Câu 2: Cho ${{z}_{1}};{{z}_{2}}$là nghiệm phương trình ${{z}^{2}}+8\left( 1-i \right)z+63-16i=0$. Tính $\left| {{z}_{1}}-{{z}_{2}} \right|$ . A. $\sqrt{65}$ B. $2\sqrt{65}$ C. $3\sqrt{65}$ D. $5\sqrt{65}$ $$ |
Lời giải: Chọn B.
Cách 1: Xét $\Delta '=16{{\left( 1-i \right)}^{2}}-\left( 63-16i \right)=-63-16i$. Ta tính $\sqrt{\Delta '}$:
.png)
.png)
.png)
.png)
Vậy $\sqrt{\Delta '}=1-8i$. Áp dụng công thức nghiệm, ta được: ${{z}_{1}}=-3-4i;{{z}_{2}}=-5+12i$.
Nên $\left| {{z}_{1}}-{{z}_{2}} \right|=2\sqrt{65}$.
Cách 2: Dùng vi-et: $$ \[\left| {{z}_{1}}-{{z}_{2}} \right|=\sqrt{\left| {{\left( {{z}_{1}}-{{z}_{2}} \right)}^{2}} \right|}=\sqrt{\left| {{\left( {{z}_{1}}+{{z}_{2}} \right)}^{2}}-4{{z}_{1}}{{z}_{2}} \right|}=\sqrt{\left| {{\left( -8\left( 1-i \right) \right)}^{2}}-4\left( 63-16i \right) \right|}=2\sqrt{65}\].
|
Câu 3: Giá trị của các số thực b, c để phương trình \[{{z}^{2}}+bz+c=0\] nhận số phức z=1+i làm một nghiệm là A.b=2; c=-2 B. b=c=-2 C. b=-2; c=2 D. b=c=2
|
Lời giải: Chọn C.
Cách 1: Vì z=1+i là nghiệm của phương trình nên ${{\left( 1+i \right)}^{2}}+b\left( 1+i \right)+c=0\Leftrightarrow b+c+\left( 2+b \right)i=0\Leftrightarrow $.png)
$\Leftrightarrow $.png)
.
Cách 2: Thử đáp án ta cũng chọn được đáp án C.
|
Câu 4: Cho z=x+yi thỏa mãn ${{z}^{3}}=18+26i$. Tìm x-y A. 2 B. 6 C. 8 D. 10 |
Lời giải: Chọn A.
Ta nhập vào máy như sau: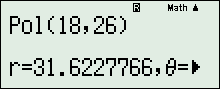 
.
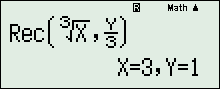Nên z=3+i. Suy ra: x-y=2.
|
Câu 5: Gọi ${{z}_{1}},{{z}_{2}},{{z}_{3}},{{z}_{4}}$là các nghiệm phương trình ${{\left( \frac{z-1}{2z-i} \right)}^{4}}=1$. Giá trị của $P=\left( z_{1}^{2}+1 \right)\left( z_{2}^{2}+1 \right)\left( z_{3}^{2}+1 \right)\left( z_{4}^{2}+1 \right)$ là A. $\frac{17}{8}$ B. $\frac{17}{9}$ C. $\frac{9}{17}$ D. $\frac{17i}{9}$
|
Lời giải: Chọn B.
${{\left( \frac{z-1}{2z-i} \right)}^{4}}=1\Leftrightarrow $.png)
$\Leftrightarrow $.png)
.
Nhập P vào máy tính và sử dụng CALC ta được P=$\frac{17}{9}$.
|
Câu 6: Giá trị m để phương trình bậc hai ${{z}^{2}}-mz+2m-1=0$ có tổng các bình phương hai nghiệm bằng -10. A. $m=2\pm 2\sqrt{2}i$ B. $m=2+2\sqrt{2}i$ C. $m=2-2\sqrt{2}i$ D. $m=-2-2\sqrt{2}i$
|
Lời giải: Chọn A.
Theo đề bài, ta có: $z_{1}^{2}+z_{2}^{2}=-10\Leftrightarrow {{\left( {{z}_{1}}+{{z}_{2}} \right)}^{2}}-2{{z}_{1}}{{z}_{2}}=-10\Leftrightarrow {{m}^{2}}-2\left( 2m-1 \right)+10=0\Leftrightarrow m=2\pm 2\sqrt{2}i$.
|
Câu 7: Biết z là nghiệm phương trình $z+\frac{1}{z}=0$. Tính ${{z}^{2019}}+\frac{1}{{{z}^{2019}}}$. A. 1 B. 2 C. 3 D. 6
|
Lời giải: Chọn A.
$z+\frac{1}{z}=1\Leftrightarrow {{z}^{2}}-z+1=0\Leftrightarrow $.png)
.
Vì 2019 là số lẻ nên thay vì tính trực tiếp ${{z}^{2019}}+\frac{1}{{{z}^{2019}}}$. Ta sẽ tính $z+\frac{1}{z}$. CALC với 1 trong 2 nghiệm ta được P=1.
|
Câu 8: Phương trình \[\left( {{z}^{2}}-z \right)\left( z+3 \right)\left( z+2 \right)=10\] có bao nhiêu nghiệm trong tập số phức. A. 1 B. 2 C. 3 D. 4
|
Lời giải: Chọn D.
\[\left( {{z}^{2}}-z \right)\left( z+3 \right)\left( z+2 \right)=10\Leftrightarrow z\left( z-1 \right)\left( z+3 \right)\left( z+2 \right)=10\Leftrightarrow \left( {{z}^{2}}+2z-3 \right)\left( {{z}^{2}}+2z \right)=10\]
Đặt \[t={{z}^{2}}+2z\]. Phương trình tương đương (t-3)t=10\[\Leftrightarrow \].png)
\[\Leftrightarrow \].png)
\[\Leftrightarrow \].png)
.
Vậy phương trình có 4 nghiệm.
|
Câu 9: ${{z}_{1}};{{z}_{2}};{{z}_{3}};{{z}_{4}}$ là nghiệm phương trình ${{z}^{4}}+\left( 4+m \right){{z}^{2}}+4m=0$. Có bao nhiêu giá trị của m để $\left| {{z}_{1}} \right|+\left| {{z}_{2}} \right|+\left| {{z}_{3}} \right|+\left| {{z}_{4}} \right|=6$. A. 0 B. 1 C. 2 D. 3 $$ |
Lời giải: Chọn C.
${{z}^{4}}+\left( 4+m \right){{z}^{2}}+4m=0\Leftrightarrow \left( {{z}^{2}}+m \right)\left( {{z}^{2}}+4 \right)=0\Leftrightarrow $.png)
.
Nếu $m\ge 0$ thì ${{z}_{3,4}}=\pm i\sqrt{-m}$. Nên $\left| {{z}_{1}} \right|+\left| {{z}_{2}} \right|+\left| {{z}_{3}} \right|+\left| {{z}_{4}} \right|=6\Leftrightarrow 4+2\sqrt{m}=6\Leftrightarrow m=1$.
Nếu m<0 thì ${{z}_{3,4}}=\pm \sqrt{-m}$. Nên $\left| {{z}_{1}} \right|+\left| {{z}_{2}} \right|+\left| {{z}_{3}} \right|+\left| {{z}_{4}} \right|=6\Leftrightarrow 4+2\sqrt{-m}=6\Leftrightarrow m=-1$.$$
Vậy có 2 giá trị m.
|
Câu 10: Phương trình ${{z}^{3}}-\left( 2-3i \right){{z}^{2}}+3\left( 1-2i \right)z+9i=0$. Biết phương trình có ${{z}_{1}}$ là 1 nghiệm thuần ảo. Tính $\left| {{z}_{1}} \right|+\left| {{z}_{2}}+{{z}_{3}} \right|$. A. 1 B. 2 C. 3 D. 5
|
Lời giải: Chọn D.
Vì ${{z}_{1}}$ là nghiệm thuần ảo nên ${{z}_{1}}=bi$. Thay vào phương trình, ta có: ${{\left( bi \right)}^{3}}-\left( 2-3i \right){{\left( bi \right)}^{2}}+3\left( 1-2i \right)\left( bi \right)+9i=0$ $\Leftrightarrow 2{{b}^{2}}+6b+\left( -{{b}^{3}}-3{{b}^{2}}+3b+9 \right)i=0\Leftrightarrow$.png)
$\Leftrightarrow $ b=-3. Vậy rút nghiệm ${{z}_{1}}=-3i$ còn lại phương trình bậc 2.
Nên ${{z}^{3}}-\left( 2-3i \right){{z}^{2}}+3\left( 1-2i \right)z+9i=0\Leftrightarrow \left( z+3i \right)\left( {{z}^{2}}-2z+3 \right)=0$ . Nên ${{z}_{2,3}}=1\pm \sqrt{2}i$.
Vậy $\left| {{z}_{1}} \right|+\left| {{z}_{2}}+{{z}_{3}} \right|$=5.
II. Bài tập tự luyện
Câu 1: Với mọi số thuần ảo z, số ${{z}^{2}}+{{\left| z \right|}^{2}}$ là:
A. Số thực âm B. Số 0
C. Số thực dương D. Số ảo khác 0
Câu 2: Trong trường số phức phương trình ${{z}^{3}}+1=0$ có mấy nghiệm
A. 0 B. 1 C. 2 D. 3
Câu 3: Số nghiệm của phương trình $4{{z}^{2}}+8{{\left| z \right|}^{2}}-3=0$.
A. 1 B. 2 C. 3 D. 4
Câu 4: Phương trình ${{z}^{6}}-9{{z}^{3}}+8=0$ có bao nhiêu nghiệm
A. 2 B. 5 C. 6 D. 8
Câu 5: Phương trình ${{z}^{4}}-{{z}^{3}}+\frac{{{z}^{2}}}{2}+z+1=0$ có bao nhiêu nghiệm
A. 1 B. 2 C. 3 D. 4
Câu 6: Tìm số thực $m=a-b\sqrt{20}$ (a, b là các số nguyên khác 0) để phương trình $2{{z}^{2}}+2\left( m-1 \right)z+\left( 2m+1 \right)=0$ có hai nghiệm thực phân biệt ${{z}_{1}};{{z}_{2}}$ thỏa mãn$\left| {{z}_{1}} \right|+\left| {{z}_{2}} \right|=\sqrt{10}$. Tìm a.
A. 1 B. 2 C. 3 D. 4
Câu 7: Số nghiệm phức của phương trình $\overline{z}+\frac{25}{z}=8-6i$ là
A. 1 B. 2 C. 3 D. 4
Câu 8: Cho 2 phương trình $a{{z}^{2}}+bz+c=0$ và $c{{z}^{2}}+bz+a+16-16i=0$ có nghiệm chung là z=1+2i. Tính a-b+c.
A. 6 B. 7 C. 8 D. 9
Câu 9: Gọi ${{z}_{1}},{{z}_{2}}$ là hai nghiệm phương trình ${{z}^{2}}-2z+2=0$. Tìm modun \[\text{w}={{\left( {{z}_{1}}-1 \right)}^{2015}}+{{\left( {{z}_{2}}-1 \right)}^{2016}}\].
A. \[\left| \text{w} \right|=\sqrt{5}\] B. \[\left| \text{w} \right|=\sqrt{2}\] C. \[\left| \text{w} \right|=1\] D. \[\left| \text{w} \right|=\sqrt{3}\]
Câu 10: Gọi M, N là điểm biểu diễn các nghiệm ${{z}_{1}},{{z}_{2}}$ của phương trình \[{{z}^{2}}+\left( 3-2i \right)z+2i-4=0\]. Chu vi \[\Delta OMN\] là
A. \[1+\sqrt{2}+\sqrt{3}\] B. \[1+2\sqrt{5}+\sqrt{29}\] C. \[1+2\sqrt{5}+\sqrt{2}\] D. \[1+2\sqrt{5}\]
Đáp án bài tập tự luyện:
.png)
