Chuyên đề sự tương giao của hàm số
Lý thuyết :
Sự tương giao của hai đồ thị:
Hoành độ giao điểm của 2 đồ thị hàm số y=f(x) và y=g(x) là nghiệm của phương trình:f(x)=g(x), (∗)
Từ đó suy ra số giao điểm của hai đồ thị đã cho bằng số nghiệm của phương trình (∗).
Bài tập minh họa :
Ví dụ 1: Cho đồ thị (C) của hàm số $y={{x}^{2}}-2x+m$ và đường thẳng (d): $y=2x+1$
- Tìm m để (d) cắt (C) tại hai điểm phân biệt A, B.
- Tìm tọa độ trung điểm I của đoạn AB.
- Tìm m để đoạn AB = 2.
Giải:
PTHĐGĐ của (C) và (d): ${{x}^{2}}-2x+m=2x+1\Leftrightarrow {{x}^{2}}-4x+m-1=0\quad (*)$
- Tìm m để (d) cắt (C) tại hai điểm phân biệt A, B:
Để có 2 giao điểm A, B phân biệt thì (*) có hai nghiệm phân biệt, do đó:
$\Delta '>0\Leftrightarrow 4-(m-1)>0\Leftrightarrow 5-m>0\Leftrightarrow m<5$
b.Tìm tọa độ trung điểm I của đoạn AB:
Khi m < 5 theo Vi-ét: ${{x}_{A}}+{{x}_{B}}=4\Rightarrow 2{{x}_{I}}={{x}_{A}}+{{x}_{B}}=4\Leftrightarrow {{x}_{I}}=2$
Vì I$\in (d)$: y = 2x + 1 nên ${{y}_{I}}=2{{x}_{I}}+1=2.2+1=5$
Vậy I (2; 5)
c. Tìm m để AB = 2:
Ta có: A$\in $(d) nên ${{y}_{A}}=2{{x}_{A}}+1$ và B$\in $(d) nên ${{y}_{B}}=2{{x}_{B}}+1$; ${{y}_{A}}-{{y}_{B}}=2\left( {{x}_{A}}-{{x}_{B}} \right)$
Ta có: $A{{B}^{2}}={{\left( {{x}_{A}}-{{x}_{B}} \right)}^{2}}+{{\left( {{y}_{A}}-{{y}_{B}} \right)}^{2}}={{\left( {{x}_{A}}-{{x}_{B}} \right)}^{2}}+4{{\left( {{x}_{A}}-{{x}_{B}} \right)}^{2}}=5{{\left( {{x}_{A}}-{{x}_{B}} \right)}^{2}}=5\left[ {{\left( {{x}_{A}}+{{x}_{B}} \right)}^{2}}-4{{x}_{A}}{{x}_{B}} \right]$
Theo Vi-ét: ${{x}_{A}}+{{x}_{B}}=4;\ {{x}_{A}}{{x}_{B}}=m-1$ nên $A{{B}^{2}}=5\left[ 16-4(m-1) \right]=5(20-4m)$
$AB=2\Leftrightarrow A{{B}^{2}}=4\Leftrightarrow 5(20-4m)=4\Leftrightarrow m=\frac{24}{5}:$ thỏa mãn m < 5
Vậy m = $\frac{24}{5}$ là giá trị cần tìm.
Ví dụ 2: Cho đồ thị (C) của hàm số $y=x+2+\frac{1}{x-1}$ và đường thẳng (d): y = mx + 3.
- Tìm m để (d) cắt (C) tại hai điểm phân biệt
b. Tìm điểm M thuộc (C) sao cho khoảng cách từ M đến trục hoành bằng 2 lần khoảng cách từ M đến trục tung.
Giải
- Phương trình hoành độ giao điểm (PTHĐGĐ) của (C) và (d):
$\frac{{{x}^{2}}+x-1}{x-1}=mx+3\Leftrightarrow {{x}^{2}}+x-1=(x-1)(mx+3)\Leftrightarrow (m-1){{x}^{2}}-(m-2)x-2=0$ (*) (x = 1 không là nghiệm của (*)
(d) cắt (C) tại hai điểm phân biệt thì .png)
Vậy giá trị m cần tìm là $m<-2-2\sqrt{2}\vee m>-2+2\sqrt{2}\quad (m\ne 1)$
b. Tìm điểm M thuộc (C):
Đặt điểm M$\left( x;x+2+\frac{1}{x-1} \right)$ thuộc (C)
Ta có: .png)
$\Leftrightarrow {{x}^{2}}-3x+1=0\quad (1)\ \ \vee \ \ 3{{x}^{2}}-x-1=0\quad (2)$
(1)$\Leftrightarrow x=\frac{3+\sqrt{5}}{2}\vee x=\frac{3-\sqrt{5}}{2}\quad \left( y=3+\sqrt{5}\vee y=3-\sqrt{5} \right)$
(2)$\Leftrightarrow x=\frac{1+\sqrt{13}}{6}\vee x=\frac{1-\sqrt{13}}{6}\quad \left( y=-\frac{1+\sqrt{13}}{3}\vee y=-\frac{1-\sqrt{13}}{3} \right)$
Vậy có bốn điểm M cần tìm là: $M\left( \frac{3+\sqrt{5}}{2};3+\sqrt{5} \right),M\left( \frac{3-\sqrt{5}}{2};3-\sqrt{5} \right),M\left( \frac{1+\sqrt{13}}{6};-\frac{1+\sqrt{13}}{3} \right),M\left( \frac{1-\sqrt{13}}{6};-\frac{1-\sqrt{13}}{3} \right)$
Ví dụ 3: Cho đồ thị (C) của hàm số $y=\frac{{{x}^{2}}+2x+2}{x+1}$ và đường thẳng (d): y = -x + m. Tìm m để (d) tiếp xúc với (C).
Giải
(d) tiếp xúc với (C) khi hệ sau có nghiệm: .png)
(2)$\Leftrightarrow 2{{x}^{2}}+4x+1=0\Leftrightarrow x=\frac{1}{2}\left( -2\pm \sqrt{2} \right)$
(1)$\Leftrightarrow m=\frac{2{{x}^{2}}+3x+2}{x+1}=\frac{(2{{x}^{2}}+4x+1)-(x+1)+2}{x+1}=-1+\frac{2}{x+1}$
+ Với $x=-1+\frac{\sqrt{2}}{2}\to m=2\sqrt{2}-1$
+ Với $x=-1-\frac{\sqrt{2}}{2}\to m=-2\sqrt{2}-1$
Vậy giá trị m cần tìm là: $m=2\sqrt{2}-1;m=-2\sqrt{2}-1$
Ví dụ 4: Cho đồ thị (C) của hàm số $y={{x}^{2}}-2x+m$. Tìm m để (C) cắt trục hoành tại hai điểm có hoành độ thỏa mãn: ${{x}_{2}}>{{x}_{1}}>-1$.
Giải
PTHĐGĐ của (C) với trục Ox: ${{x}^{2}}-2x+m=0$ (*). Để có hai giao điểm có hoành độ thỏa mãn: ${{x}_{2}}>{{x}_{1}}>-1$ thì ta phải có:
$\Delta '>0\Leftrightarrow 1-m>0\Leftrightarrow m<1$ ${{x}_{1}}>-1\Leftrightarrow 1-\sqrt{1-m}>-1\Leftrightarrow 2>\sqrt{1-m}\Leftrightarrow 4>1-m\Leftrightarrow m>-3$
Vậy giá trị m cần tìm là: .png)
Ví dụ 5: Tìm m để đồ thị (C) của hàm số $y=m{{x}^{3}}+{{x}^{2}}-2x-8m$
- Tiếp xúc với trục hoành.
b. Cắt trục hoành tại ba điểm phân biệt có hoành độ thỏa x > 1.
Giải
a. Tìm m để (C) tiếp xúc với trục hoành:
Đồ thị (C) tiếp xúc vơi trục hoành khi hệ sau có nghiệm:.png)
.png)
+ Hệ (I) có nghiệm khi: $3m{{.2}^{2}}+2.2-2=0\Leftrightarrow m=-\frac{1}{6}$
+ Xét sự có nghiệm của hệ (II): .png)
Từ (2) ta có: $m=\frac{2-2x}{3{{x}^{2}}}$ thay vào (1) được: $\frac{2-2x}{3{{x}^{2}}}.{{x}^{2}}+\left( 2.\frac{2-2x}{3{{x}^{2}}}+1 \right)x+4.\frac{2-2x}{3{{x}^{2}}}=0$
$\Leftrightarrow {{(x-2)}^{2}}(x+2)=0\Leftrightarrow x=2\Rightarrow m=-\frac{1}{6}\vee x=-2\Rightarrow m=\frac{1}{2}$
Vậy (C) tiếp xúc với trục hoành khi $m=-\frac{1}{6}\vee m=\frac{1}{2}$
b. Tìm m để (C) cắt trục hoành tại ba điểm phân biệt có hoành độ thỏa x > 1
Phương trình hoành độ giao điểm của (C) và trục hoành: $m{{x}^{3}}+{{x}^{2}}-2x-8m=0$ (1)
.png)
(C) cắt trục hoành tại ba điểm phân biệt có hoành độ thỏa x > 1 khi (1) có ba nghiệm phân biệt x > 1, tức là (2) có hai nghiệm phân biệt $x\ne 2\ v\text{ }\!\!\grave{\mathrm{a}}\!\!\text{ }\ {{x}_{2}}>{{x}_{1}}>1$
+ Điều kiện (2) có hai nghiệm phân biệt $x\ne 2$ khi .png)
.png)
+ Điều kiện (2) có hai nghiệm ${{x}_{2}}>{{x}_{1}}>1$:
(2) có nghiệm: $x=\frac{-(2m+1)\pm \sqrt{(6m+1)(1-2m)}}{2m}$
- Trường hợp: .png)
${{x}_{1}}=\frac{-(2m+1)-\sqrt{(6m+1)(1-2m)}}{2m}>1\Leftrightarrow -(2m+1)-\sqrt{(6m+1)(1-2m)}>2m$ (3)
(3) vô nghiệm vi: Vế trái có giá trị âm, vế phải có giá trị dương.
- Trường hợp: .png)
${{x}_{1}}=\frac{-(2m+1)+\sqrt{(6m+1)(1-2m)}}{2m}>1\Leftrightarrow -(2m+1)+\sqrt{(6m+1)(1-2m)}<2m$
$\Leftrightarrow \sqrt{(6m+1)(1-2m)}<4m+1\Leftrightarrow (6m+1)(1-2m)<{{(4m+1)}^{2}}\Leftrightarrow 28{{m}^{2}}+4m>0\Leftrightarrow m<-\frac{1}{7}\vee m>0$Vậy giá trị m cần tìm là: .png)
Bài tập tự luyện :
Câu 1: Cho hàm số \[y={{x}^{3}}-4x\]. Số giao điểm của đồ thị hàm số và trục Ox bằng
A. 0 B. 2 C. 3 D. 4
Câu 2: Số giao điểm của đường cong \[y={{x}^{3}}-2{{\text{x}}^{2}}+2\text{x}+1\] và đường thẳng \[y=1-x\] bằng
A. 0 B. 2 C. 3 D. 1
Câu 3: Gọi M, N là giao điểm của đường thẳng y = x + 1 và đường cong \[y=\frac{2x+4}{x-1}\]. Khi đó hoành độ trung điểm I của đoạn thẳng MN bằng
A. \[-\frac{5}{2}\] B. 1 C. 2 D. \[\frac{5}{2}\]
Câu 4: Cho hàm số \[y={{x}^{3}}-3{{\text{x}}^{2}}+2\]. Đồ thị hàm số cắt đường thẳng y = m tại 3 điểm phân biệt
A. -3 < m < 1 B. -3 ≤ m ≤ 1 C. m > 1 D. m < 3
Câu 5: Đường thẳng y = m cắt đồ thị hàm số \[y={{x}^{3}}-3{{\text{x}}^{2}}+2\] tại 3 điểm phân biệt khi
A. m > 4 B. 0 ≤ m < 4 C. 0 < m ≤4 D. 0 < m < 4
Câu 6: Đường thẳng y = m không cắt đồ thị hàm số \[y=-2{{\text{x}}^{4}}+4{{\text{x}}^{2}}+2\] khi
A. 0 < m < 4 B. m > 4 C. m < 0 D. m = 0; m = 4
Câu 7: Cho hàm số \[y=\frac{2x+1}{x+1}\] có đồ thị (C). Tìm các giá trị của m để đường thẳng d: y = x + m - 1 cắt đồ thị hàm số (C) tại hai điểm phân biệt A, B sao cho 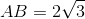
A. 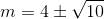
B. 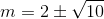
C. 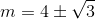
D. 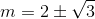
Câu 8: Với giá trị nào của m được liệt kê bên dưới thì đồ thị hàm số \[y={{\text{x}}^{4}}\text{- 8}{{\text{x}}^{2}}+3\] cắt đường thẳng y = 4m tại 4 điểm phân biệt:
A. \[-\frac{13}{4}
B. \[-\frac{13}{4}\le m\le \frac{13}{4}\]
C. \[m\le \frac{3}{4}\]
D. \[m\ge -\frac{13}{4}\]
Câu 9: Cho hàm số \[y=\frac{2x+3}{x+2}\] có đồ thị (C) và đường thẳng d: y = x + m với giá trị nào của m thì d cắt (C) tại hai điểm phân biệt
A. m < 2 B. m > 6 C. 2 < m < 6 D. m < 2 hoặc m > 6
Câu 10: Đồ thị hàm số nào sau đây cắt trục tung tại điểm có tung độ âm?
A. \[y=\frac{-2\text{x}+3}{x+1}\] B. \[y=\frac{\text{3x}+4}{x-1}\] C. \[y=\frac{\text{4x}+1}{x+2}\] D. \[y=\frac{2x-3}{3x-1}\]
Câu 11: Hoành độ giao điểm của parabol \[(P):y=\frac{1}{4}{{x}^{2}}-2x\]và đường thẳng \[\,d:y=\frac{3}{4}x-6\] là:
A. 2 và 6 B. 1 và 7 C. 3 và 8 D. 4 và 5
Câu 12: Cho hàm số \[y={{x}^{3}}-6{{x}^{2}}+9\text{x}-1\] có đồ thị (C). Đường thẳng y = 3 cắt (C) tại mấy điểm?
A. 3 B. 2 C. 1 D. 0
Câu 13: Cho hàm số \[y=(x-2)({{x}^{2}}+m\text{x}+{{m}^{2}}-3)\] có đồ thị (\[{{C}_{m}}\]). Với giá trị nào của m thì (\[{{C}_{m}}\]) cắt Ox tại 3 điểm phân biệt?
A. – 2 < m < 2 B. – 2 < m < – 1 C. – 1 < m < 2 D. -2 < m < 2 và m ≠ -1
Câu 14: Cho hàm số \[y={{x}^{4}}-5{{\text{x}}^{2}}+4\]. Với các giá trị nào của m thì đồ thị hàm số cắt đường thẳng d: y = m tại bốn điểm phân biệt
A. \[m>-\frac{9}{4}\] B. \[m<-\frac{9}{4}\] C. .png) D.
D. .png)
Câu 15: Đồ thị hàm số \[y=\frac{{{x}^{2}}-4x+4}{x+1}\] có mấy điểm chung với trục Ox
A. 0 B. 1 C. 2 D. 3
ĐÁP ÁN
.png)







