Chuyên đề khối tròn xoay – hình nón - mặt nón – khối nón
I. Khái niệm về mặt tròn xoay :
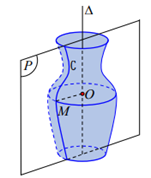
1. Trục của đường tròn (O R; ) : là đường thẳng đi qua tâm O và vuông góc với mặt phẳng chứa đường tròn.
2. Trong không gian cho mặt phẳng (P) chứa đường thẳng D và một đường C . Khi quay mặt phẳng (P) quanh D một góc 360° thì mỗi điểm M trên C vạch ra một đường tròn có tâm O thuộc D và nằm trên mặt phẳng vuông góc với D . Như vậy khi quay mặt phẳng (P) quanh đường thẳng D thì C sẽ tạo nên được một hình gọi là mặt tròn xoay. Trong đó: đường C được gọi là đường sinh; đường thẳng D được gọi là trục của mặt tròn xoay.
II. Mặt nón – Hình nón – Khối nón :
1. Định nghĩa mặt nón:
Trong mặt phẳng (P) cho hai đường thẳng d và D cắt nhau tại điểm O và tạo thành góc a\[\left( {{0}^{o}}<\alpha <{{90}^{o}} \right)\]. Khi quay mặt phẳng (P) xung quanh D thì đường thẳng d sinh ra một mặt tròn xoay được gọi là mặt nón tròn xoay đỉnh O. Gọi tắt là mặt nón.
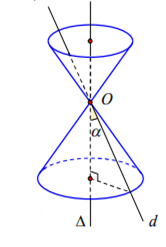
· ∆ gọi là trục của mặt nón.
· d gọi là đường sinh của mặt nón.
· O gọi là đỉnh của mặt nón.
· Nếu gọi a là góc giữa d và D thì 2a gọi là góc ở đỉnh của mặt nón.
2. Hình nón tròn xoay:
· Cho DIOM vuông tại I . Khi quay tam giác đó xung quanh cạnh vuông góc OI thì đường gấp khúc IOM tạo thành một hình được gọi là hình nón tròn xoay, gọi tắt là hình nón.
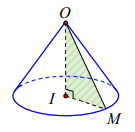
· Trong đó
- Hình tròn tâm I sinh bởi các điểm thuộc cạnh IM khi IM quay quanh trục OI được gọi là mặt đáy của mình nón.
- Điểm O được gọi là đỉnh của hình nón.
- Độ dài đoạn OI được gọi là chiều cao của hình nón.
- Độ dài đoạn OM được gọi là độ dài đường sinh của hình nón.
- Phần mặt tròn xoay sinh bởi các điểm trên cạnh OM khi quay quanh OI được gọi là mặt xung quanh của hình nón.
3. Khối nón tròn xoay:
· Phần không gian được giới hạn bởi một hình nón tròn xoay kể cả hình đó được gọi là khối nón tròn xoay hay còn gọi tắt là khối nón.
· Trong đó:
- Điểm thuộc khối nón nhưng không thuộc hình nón gọi là điểm trong của khối nón.
- Ta gọi đỉnh, mặt đáy, đường sinh của hình nón theo thứ tự là đỉnh, mặt đáy, đường sinh của khối nón tương ứng.
4. Diện tích hình nón và thể tích khối nón:
a. Định nghĩa:
· Diện tích xung quanh của hình nón là giới hạn của diện tích xung quanh của hình chóp đều nội tiếp hình nón đó khi số cạnh đáy tăng lên vô hạn.
· Thể tích của khối nón là giới hạn của thể tích của hình chóp đều nội tiếp hình nón đó khi số cạnh đáy tăng lên vô hạn.
b. Công thức:
Gọi r là bán kính đường tròn đáy; l là độ dài đường sinh; h là chiều cao; B là diện tích đáy của hình nón.
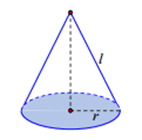
· Diện tích xung quanh : \[{{S}_{xq}}=\pi rl\]
· Diện tích toàn phần : \[{{S}_{tp}}=\pi {{r}^{2}}+\pi rl\]
· Thể tích khối nón : \[V=\frac{1}{3}B.h=\frac{1}{3}\pi {{r}^{2}}h\]
5. Hình nón cụt :
a. Định nghĩa :Hình nón cụt là phần nón giới hạn bởi mặt đáy và một thiết diện song song với đáy.
b. Công thức:
· Diện tích xung quanh : \[{{S}_{xq}}=\pi \left( R+r \right)l\]
· Diện tích toàn phần : \[{{S}_{tp}}=\pi \left( {{R}^{2}}+{{r}^{2}} \right)+\pi \left( R+r \right)l\]
· Thể tích khối nón cụt : \[V=\frac{1}{3}\pi h\left( {{R}^{2}}+{{r}^{2}}+R\text{r} \right)\]
Trong đó: R r, là bán kính hai đáy; h = là độ cao hình nón cụt.
6. Thiết diện hình nón :
Cắt mặt nón tròn xoay bởi mặt phẳng ( P) . Nếu:
a) Mặt phẳng ( P) không qua đỉnh thì thiết diện là:
- Một elip nếu ( P) cắt tất cả các đường sinh. Đặc biệt nếu ( P) vuông góc với trục của mặt nón thì thiết diện là đường tròn.
- Một đường Parabol nếu ( P) song song với chỉ một đường sinh.
- Một đường Hypebol nếu ( P) song song với hai đường sinh.
b) Mặt phẳng ( P) qua đỉnh thì thiết diện là:
- Tam giác cân tại đỉnh của hình nón nếu ( P) cắt mặt nón theo 2 đường sinh.
- Mặt tiếp xúc với mặt nón theo một đường sinh.
III. Một số bài tập mẫu :
Công thức và phương pháp làm bài :
1. Hình nón:
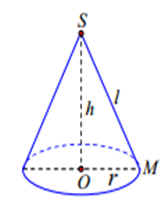
- Chiều cao : \[SO=h\]
- Đường sinh : \[SM=l\]
- Góc ở đỉnh : \[\overset\frown{M\text{S}N}=2\text{a}\]
- Bán kính đáy là r thì : \[{{l}^{2}}={{r}^{2}}+{{h}^{2}}\]
- Diện tích xung quanh : \[{{S}_{xq}}=\pi rl\]
- Diện tích toàn phần : \[{{S}_{tp}}=\pi {{r}^{2}}+\pi rl\]
- Thể tích : \[V=\frac{1}{3}Bh=\frac{1}{3}\pi {{r}^{2}}h\]
2. Hình nón cụt :
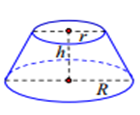Diện tích xung quanh :\[{{S}_{xq}}=\pi \left( R+r \right)l\]- Diện tích toàn phần :\[{{S}_{tp}}=\pi \left( {{r}^{2}}+{{R}^{2}} \right)+\pi \left( R+r \right)l\]
- Thể tích : \[V=\frac{1}{3}\pi h\left( {{R}^{2}}+{{r}^{2}}+R\text{r} \right)\]
Bài toán 1 : Cho tam giác ABC vuông tại A, AB=a và AC=a√3. Tính độ dài đường sinh của hình nón , nhận được khi quay tam giác ABC xung quanh trục AB.
Giải
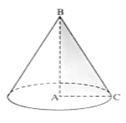
Theo Py-ta-go ta có : \[A{{B}^{2}}+A{{C}^{2}}=B{{C}^{2}}\]
\[\Rightarrow B{{C}^{2}}={{a}^{2}}+3{{\text{a}}^{2}}=4{{\text{a}}^{2}}\]
\[\Rightarrow BC=2\text{a}\]
Vậy độ dài đường sinh BC = 2a
Bài toán 2 : Cho tam giác ABC vuông tại A , AB = 3 và AC = 4 . Tính độ dài đường sinh l của hình nón nhận được khi quay tam giác ABC xung quanh trục AC .
Giải
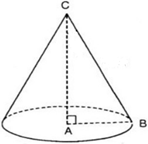
Theo Py-ta-go ta có : \[A{{B}^{2}}+A{{C}^{2}}=B{{C}^{2}}\]
\[\Rightarrow B{{C}^{2}}={{3}^{2}}+{{4}^{2}}=25\]
\[\Rightarrow BC=5\]
Vậy độ dài đường sinh BC = 5
Bài toán 3 : Cho hình nón có bán kính đáy r = 3cm và đường sinh l = 5cm .
a) Tính độ dài đường sinh , diện tích xung quanh và diện tích toàn phần của hình nón.
b) Tính thể tích của khối nón tương ứng.
Giải
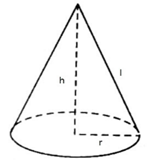
a) Theo Py-ta-go, ta có : \[{{h}^{2}}+{{r}^{2}}={{l}^{2}}\]
\[\Rightarrow {{h}^{2}}={{l}^{2}}-{{r}^{2}}={{5}^{2}}-{{3}^{2}}=16\]
\[\Rightarrow h=4\,cm\]
- Diện tích xung quanh : \[{{S}_{xq}}=\pi rl=\pi .3.5=15\pi \,\left( c{{m}^{2}} \right)\]
- Diện tích toàn phần : \[{{S}_{tp}}=\pi {{r}^{2}}+\pi rl\]
\[\Rightarrow {{S}_{tp}}=\pi {{.3}^{2}}+\pi .3.5=9\pi +15\pi =24\pi \left( c{{m}^{2}} \right)\]
b) Thể tích khối nón : \[V=\frac{1}{3}.B.h=\frac{1}{3}.\pi .{{r}^{2}}.h=\frac{1}{3}.\pi .9.5=15\pi \left( c{{m}^{3}} \right)\]
Bài toán 4 : Các bán kính đáy của một hình nón cụt lần lượt là a và 3a , đường sinh là 2,9a . Tính thể tích khối nón cụt đó.
Giải
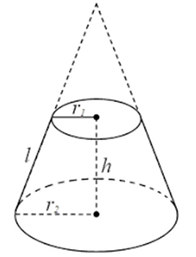
Ta có : \[{{r}_{1}}=a\,,\,\,{{r}_{2}}\,=3\text{a}\,,\,l=2,9\text{a}\]
\[{{h}^{2}}={{l}^{2}}-{{\left( {{r}_{2}}-{{r}_{1}} \right)}^{2}}\]
\[\Rightarrow {{h}^{2}}=\,8,41{{\text{a}}^{2}}-4{{\text{a}}^{2}}=4,41{{a}^{2}}\]
\[\Rightarrow h=2,1\text{a}\]
-Thể tích khối nón cụt :
\[V=\frac{1}{3}\pi h\left( r_{2}^{2}+r_{1}^{2}+{{r}_{1}}{{r}_{2}} \right)\]
\[\Rightarrow V=\frac{1}{3}\pi .2,1\text{a}\left( 9{{\text{a}}^{2}}+{{a}^{2}}+3{{\text{a}}^{2}} \right)\]
\[\Rightarrow V=9,1\pi {{a}^{3}}\]
IV. Một số bài tập tự luyện :
Câu 1: Cho hình nón có thiết diện qua trục là một tam giác đều cạnh 2a , diện tích xung quanh là S1 và mặt cầu có đường kính bằng chiều cao hình nón, có diện tích S2 . Khẳng định nào sau đây là khẳng định đúng ?
A.\[2{{\text{S}}_{2}}=3{{\text{S}}_{1}}\]
B.\[{{S}_{1}}=4{{\text{S}}_{2}}\]
C.\[{{\text{S}}_{2}}=2{{\text{S}}_{1}}\]
D.\[{{S}_{1}}={{\text{S}}_{2}}\]
Câu 2 : Cho hình nón có thiết diện qua trục là một tam giác đều cạnh 2a , có thể tích \[{{V}_{1}}\] và hình cầu có đường kính bằng chiều cao hình nón, có thể tích \[{{V}_{2}}\]. Khi đó, tỉ số thể tích \[\frac{{{V}_{1}}}{{{V}_{2}}}\] bằng bao nhiêu?
A.\[\frac{{{V}_{1}}}{{{V}_{2}}}=\frac{2}{3}\]
B.\[\frac{{{V}_{1}}}{{{V}_{2}}}=1\]
C.\[\frac{{{V}_{1}}}{{{V}_{2}}}=\frac{1}{2}\]
D.\[\frac{{{V}_{1}}}{{{V}_{2}}}=\frac{1}{3}\]
Câu 3 : Tính diện tích xung quanh của hình trụ biết hình trụ có bán kính đáy a và đường cao là a√3.
A.\[2\pi {{a}^{2}}\]
B.\[2\pi {{a}^{2}}\sqrt{3}\]
C.\[\pi {{a}^{2}}\]
D.\[\pi {{a}^{2}}\sqrt{3}\]
Câu 4 : Một hình nón có thiết diện qua trục là một tam giác vuông cân có cạnh góc vuông bằng a . Tính diện tích xung quanh của hình nón.
A.\[\frac{\pi {{a}^{2}}\sqrt{2}}{4}\]
B.\[\frac{\pi {{a}^{2}}\sqrt{2}}{2}\]
C.\[\pi {{a}^{2}}\sqrt{2}\]
D.\[\frac{2\pi {{a}^{2}}\sqrt{2}}{3}\]
Câu 5 : Thiết diện đi qua trục của hình nón đỉnh S là tam giác vuông cân SAB có cạnh cạnh huyền bằnga√2 . Diện tích toàn phần của hình nón và thể tích V của khối nón tương ứng đã cho là
A. \[{{S}_{tp}}=\frac{\pi {{a}^{2}}\left( 1+\sqrt{2} \right)}{2};V=\frac{\pi {{a}^{3}}\sqrt{2}}{12}\]
B. \[{{S}_{tp}}=\frac{\pi {{a}^{2}}\sqrt{2}}{2};V=\frac{\pi {{a}^{3}}\sqrt{2}}{4}\]
C. \[{{S}_{tp}}=\pi {{a}^{2}}\left( 1+\sqrt{2} \right);V=\frac{\pi {{a}^{3}}\sqrt{2}}{6}\]
D. \[{{S}_{tp}}=\frac{\pi {{a}^{2}}\left( \sqrt{2}-1 \right)}{2};V=\frac{\pi {{a}^{3}}}{12}\]
Câu 6 : Cho hình nón tròn xoay có đỉnh là S , O là tâm của đường tròn đáy, đường sinh bằng a√2 và góc giữa đường sinh và mặt phẳng đáy bằng 60° . Diện tích xung quanh của hình nón và thể tích V của khối nón tương ứng là:
A. \[{{S}_{xq}}=\pi {{a}^{2}};V=\frac{\pi {{a}^{3}}\sqrt{6}}{12}\]
B. \[{{S}_{xq}}=\frac{\pi {{a}^{2}}}{2};V=\frac{\pi {{a}^{3}}\sqrt{3}}{12}\]
C. \[{{S}_{xq}}=\pi {{a}^{2}}\sqrt{2};V=\frac{\pi {{a}^{3}}\sqrt{6}}{4}\]
D. \[{{S}_{xq}}=\pi {{a}^{2}};V=\frac{\pi {{a}^{3}}\sqrt{6}}{4}\]
Câu 7 : Một hình nón có đường kính đáy là 2a√3 , góc ở đỉnh là 120° . Tính thể tích của khối nón đó theo a .
A.\[3\pi {{a}^{3}}\] B.\[\pi {{a}^{3}}\] C.\[2\sqrt{3}\pi {{a}^{3}}\] D.\[\sqrt{3}\pi {{a}^{3}}\]
Câu 8 : Trong không gian, cho tam giác ABC vuông tại A , AB=a và AC=√3a . Tính độ dài đường sinh l của hình nón, nhận được khi quay tam giác ABC xung quanh trục AB .
A.l=a B.l=a√2 C.l=a√3 D.l=2a
Câu 9 : Một hình nón có chiều cao h = 20 cm, bán kính đáy r = 25 cm. Một thiết diện đi qua đỉnh có khoảng cách từ tâm của đáy đến mặt phẳng chứa thiết diện là 12 cm. Tính diện tích thiết diện đó.
A.\[450\sqrt{2}\,c{{m}^{2}}\] B.\[500\sqrt{2}\,c{{m}^{2}}\] C.\[500\,c{{m}^{2}}\] D.\[125\sqrt{34}\,c{{m}^{2}}\]
Câu 10 :. Cho hình lập phương ABCD.A’B’C’D’ có cạnh là a . Hãy tính diện tích xung quanh Và thể tích của khối nón có đỉnh là tâm O của hình vuông ABCD và đáy là hình tròn nội tiếp hình vuông A’B’C’D’.
A. \[{{S}_{xq}}=\frac{\pi {{a}^{2}}\sqrt{5}}{2}\,;V=\frac{\pi {{a}^{3}}}{12}\]
B. \[{{S}_{xq}}=\frac{\pi {{a}^{2}}\sqrt{5}}{4}\,;V=\frac{\pi {{a}^{3}}}{4}\]
C. \[{{S}_{xq}}=\frac{\pi {{a}^{2}}\sqrt{3}}{2}\,;V=\frac{\pi {{a}^{3}}}{6}\]
D. \[{{S}_{xq}}=\pi {{a}^{2}}\sqrt{5};V=\frac{\pi {{a}^{3}}}{4}\]
Đáp án :
