
CHUYÊN ĐỀ: LŨY THỪA- HÀM
SỐ LŨY THỪA
A.
Lũy thừa:
I.
Lý thuyết:
1.
Lũy thừa với số mũ nguyên:
a) Định nghĩa:
·
Lũy thừa với số mũ nguyên dương, cho \[a\in
R,n\in {{N}^{*}}\], khi đó:\[{{a}^{n}}=a.a.a......a\] ( tích n thừa số a)
·
Lũy thừa với số mũ nguyên âm:\[{{a}^{0}}=1;{{a}^{-n}}=\frac{1}{{{a}^{n}}}\]
(\[\forall a\ne 0\])
·
\[{{0}^{0}},{{0}^{n}}\] không có nghĩa.
b) Tính chất:
·
Về đẳng
thức: Cho \[a>0;m,n\in R\]. Khi đó ta có:
\[1.{{a}^{m}}{{a}^{n}}={{a}^{m+n}}\] ; \[2.\frac{{{a}^{m}}}{{{a}^{n}}}={{a}^{m-n}}\] ; \[3.{{({{a}^{m}})}^{n}}={{({{a}^{n}})}^{m}}={{a}^{m.n}}\]
\[4.{{(a.b)}^{n}}={{a}^{n}}.{{b}^{n}}\] ; \[5.{{\left( \frac{a}{b}
\right)}^{n}}=\frac{{{a}^{n}}}{{{b}^{n}}}\]
·
Về bất đẳng thức:
Cho
m,n là các số nguyên dương ta có:
-
Với \[a>1\]thì \[{{a}^{m}}>{{a}^{n}}\Leftrightarrow
m>n\]
-
Với \[0
-
Với \[a>0\]thì \[{{a}^{m}}={{a}^{n}}\Leftrightarrow
m=n\]
Cho \[0<>
-
Với \[{{a}^{m}}<{{b}^{m}}\Leftrightarrow
m>0\]
-
Với \[{{a}^{m}}>{{b}^{m}}\Leftrightarrow
m<0\]
2. Căn bậc n:
a) .Định nghĩa:
·
Cho số
thực b và số nguyên dương n,sô a được gọi là căn bậc n của b
nếu \[{{a}^{n}}=b\]
·
Với n lẻ và , có duy nhất 1 căn bậc n
của b, kí hiệu \[\sqrt[n]{b}\]
·
Với n chẵn:
-
\[b<0\]: không tồn tại căn bậc n của
b
-
\[b=0:\sqrt[n]{b}=0\]
-
\[b>0\]: có 2 căn trái dấu kí hiệu
giá trị dương là\[\sqrt[n]{b}\], giá trị âm là \[-\sqrt[n]{b}\]
b) Tính chất:
Cho \[a,b\in R;m,n\in Z;(m,n\ge 2)\]khi
đó, ta có:
\[1.\sqrt[n]{a}.\sqrt[n]{b}=\sqrt[n]{a.b}\] ;
\[2.\frac{\sqrt[n]{a}}{\sqrt[n]{b}}=\sqrt[n]{\frac{a}{b}}\] ;
\[3.\sqrt[n]{\sqrt[m]{a}}=\sqrt[n.m]{a}\]
\[4.\sqrt[n]{{{a}^{n}}}\](
= a khi n lẻ; = |a| khi n chẵn)
\[5.{{\left( \sqrt[n]{a}
\right)}^{m}}=\sqrt[n]{{{a}^{m}}}={{a}^{\frac{m}{n}}}(a>0)\]
Chú ý:
nếu m,n là số chẵn thì cơ số a, b phải thỏa mãn để căn thức có nghĩa.
1.
Lũy thừa với số mũ hữu tỉ:
a) Định nghĩa:
Cho số thực a dương và số hữu tỉ \[r=\frac{m}{n}\],
trong đó \[\]\[m\in Z,n\in N,n\ge 2\]. Lũy thừa của a với số mũ r là số \[{{a}^{r}}\]xác
định bởi: \[{{a}^{r}}={{a}^{\frac{m}{n}}}=\sqrt[n]{{{a}^{m}}}\]
b) Tính chất:
Lũy thừa với số mũ hữu tỉ có đầy đủ tính chất
như lũy thừa với số mũ nguyên.
2.
Lũy thừa với số mũ thực:
a) Định nghĩa:
Cho số thực dương a và \[\alpha \]là
số vô tỉ. Khi đó tồn tại dãy số hữu tỉ \[({{r}_{n}})\]có giới hạn \[\alpha \And
{{a}^{\alpha }}=\underset{n\to \infty }{\mathop{\lim }}\,{{a}^{{{r}_{n}}}}\]
b) Tính chất:
Lũy thừa với số mũ thực có đầy đủ tính chất
như lũy thừa với số mũ nguyên.
Chú ý:
·
Luỹ thừa với số mũ nguyên dương thì cơ số bất
kì.
·
Luỹ thừa với số mũ 0 hoặc nguyên âm thì cơ số
khác 0.
·
Luỹ thừa với số mũ không nguyên thì cơ số
dương.
II.
Ví dụ minh họa:
Câu 1: Cho số thực \[\]\[a\ne 0\]. Với giá trị
nào cùa x thì đẳng thức \[\frac{1}{2}({{a}^{x}}+{{a}^{-x}})=1\]đúng?
A. \[x=1\] B. \[x=0\] C. \[x=a\] D. \[x=\frac{1}{a}\]
Giải: ta có \[\frac{1}{2}({{a}^{x}}+{{a}^{-x}})=1\Leftrightarrow
{{a}^{x}}+\frac{1}{ax}=2\Leftrightarrow {{({{a}^{x}})}^{2}}-2{{a}^{x}}+1=0\]
\[\Leftrightarrow
{{({{a}^{x}}-1)}^{2}}=0\Leftrightarrow {{a}^{x}}=1\Leftrightarrow x=0\] =>
chọn B
Câu 2: Tìm tất cả các giá trị của a thỏa mãn \[\sqrt[15]{{{a}^{7}}}>\sqrt[5]{{{a}^{2}}}\]
A. \[a=0\] B. \[a<0\] C. \[a>1\] D.
\[0<>
Giải: ta có \[\sqrt[15]{{{a}^{7}}}>\sqrt[5]{{{a}^{2}}}\Leftrightarrow
{{a}^{\frac{7}{15}}}>{{a}^{\frac{2}{5}}}\Leftrightarrow
{{a}^{\frac{7}{15}}}>{{a}^{\frac{6}{15}}}\to a>1\]
=>chọn C
Câu 3: Rút gọn biểu thức \[K={{\left(
{{x}^{\frac{1}{2}}}-{{y}^{\frac{1}{2}}} \right)}^{2}}{{\left(
1-2\sqrt{\frac{y}{x}}+\frac{y}{x} \right)}^{-1}}(x>0,y>0)\]
A. K=x B. K=2x C. K=x+1 D. K=x-1
Giải:
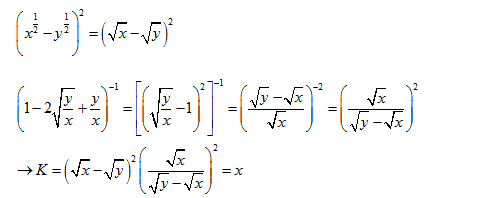
ð Chọn
A
Câu 4: Rút gọn biểu thức \[p=\frac{{{a}^{\sqrt{3}+1}}.{{a}^{2-\sqrt{3}}}}{{{({{a}^{\sqrt{2}-2}})}^{\sqrt{2}+2}}}(a>0)\]
A. \[P={{a}^{4}}\] B. \[P=a\] C. \[P={{a}^{5}}\] D.
\[P={{a}^{3}}\]
Giải:
\[p=\frac{{{a}^{\sqrt{3}+1}}.{{a}^{2-\sqrt{3}}}}{{{({{a}^{\sqrt{2}-2}})}^{\sqrt{2}+2}}}=\frac{{{a}^{\sqrt{3}+1+(2-\sqrt{3})}}}{{{a}^{(\sqrt{2}-2)(\sqrt{2}+2)}}}=\frac{{{a}^{3}}}{{{a}^{-2}}}={{a}^{3-(-2)}}={{a}^{5}}\]=>
chọn C
Câu 5: Với giá trị nào của a thì đẳng thức\[\sqrt{a\sqrt[3]{a\sqrt[4]{a}}}=\sqrt[24]{{{2}^{5}}}.\frac{1}{\sqrt{{{2}^{-1}}}}\] đúng
A. a=2 B. a=-2 C. a=3 D. a=-3
Giải:
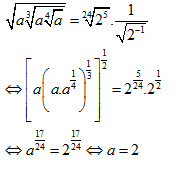
ð Chọn
A
III.
Bài tập luyện tập:
Câu
1: Rút
gọn biểu thức \[Q=b\frac{5}{3}:\sqrt[3]{b}(b>0)\]
A. \[Q={{b}^{2}}\] B. \[Q={{b}^{-\frac{4}{3}}}\]
C. \[Q={{b}^{-2}}\] D. \[Q={{b}^{\frac{4}{3}}}\]
Câu
2: Cho
biểu thức \[P=\sqrt[3]{{{x}^{2}}\sqrt{x\sqrt[5]{{{x}^{3}}}}}(x>0)\]. Mệnh đề
nào dưới đây là \[\]mệnh đề đúng
A. \[P={{x}^{\frac{14}{15}}}\] B. \[P={{x}^{4}}\]
C. \[P={{x}^{-4}}\] D. \[P={{x}^{-\frac{15}{14}}}\]
Câu
3: Khẳng
định nào sau đây sai?
A.
\[{{8}^{\frac{2}{3}}}=4\] B. \[{{8}^{\frac{2}{3}}}=\sqrt{{{8}^{3}}}\] C. \[{{8}^{\frac{2}{3}}}=\sqrt[3]{64}\] D. \[{{8}^{\frac{2}{3}}}={{(\sqrt[3]{8})}^{2}}\]
Câu
4: Cho
x là số thực dương. Viết biểu thức\[Q=\sqrt{x\sqrt[3]{{{x}^{2}}}}.\sqrt[6]{x}\]
dưới dạng lũy thừa với số mũ hữu tỉ
A.
\[Q={{x}^{\frac{5}{36}}}\] B. \[Q={{x}^{\frac{2}{3}}}\] C. \[Q=x\] D. \[Q={{x}^{2}}\]
Câu
5: Biểu
thức thu gọn của biểu thức\[P=\left( \frac{{{a}^{\frac{1}{2}}}+2}{a+2{{a}^{\frac{1}{2}}}+1}-\frac{{{a}^{\frac{1}{2}}}-2}{a-1}
\right).\frac{{{a}^{\frac{1}{2}}}+1}{{{a}^{\frac{1}{2}}}}\left( a>0,a\ne \pm
1 \right)\]có dạng \[P=\frac{m}{a+n}\]. Tính m-n
A.
1 B.
3 C.
2 D. -3
Câu
6: Cho
a, b là hai số thực dương, và biểu thức \[P=\frac{\sqrt[3]{8{{a}^{3}}{{b}^{6}}}{{({{a}^{-2}}{{b}^{-3}})}^{2}}}{\sqrt[4]{{{a}^{6}}{{b}^{-12}}}}\].
Rút gọn biểu thức P, ta được kết quả nào trong các kết quả sau:
A.
\[P=\frac{2}{{{b}^{3}}.\sqrt{a}}\]
B. \[P=\frac{2}{{{a}^{4}}b\sqrt{a}}\] C. \[P=\frac{2}{2b\sqrt{{{a}^{3}}}}\] D. \[P=2b\sqrt{{{a}^{3}}}\]
Câu
7: Cho
\[a>1>b>0\]. Khẳng định nào sau đây đúng:
A.
\[{{a}^{2}}<{{b}^{2}}\] B. \[{{a}^{-\sqrt{3}}}<{{b}^{-\sqrt{3}}}\]
C. \[{{b}^{-2}}>{{b}^{-e}}\] D. \[{{a}^{-2}}<{{a}^{-3}}\]
Câu
8: Tính
giá trị của biểu thức \[K=\frac{{{2}^{3}}{{.2}^{-1}}+{{5}^{-3}}.54}{{{10}^{-3}}:{{10}^{-2}}-{{(0.25)}^{0}}}\]
A.
-10 B. 10 C. 12 D. 15
Câu
9: Mệnh
đề nào dưới đây đúng với mọi số thực x, y
A.
\[{{({{2}^{x}})}^{y}}={{2}^{x+y}}\] B. \[\frac{{{2}^{x}}}{{{2}^{y}}}={{2}^{\frac{x}{y}}}\] C. \[{{2}^{x}}{{.2}^{y}}={{2}^{x+y}}\] D. \[{{\left( \frac{2}{3}
\right)}^{x}}=\frac{{{2}^{x}}}{3}\]
Câu
10: Với
các số thực a, b bất kì. Mệnh đề sau đây là đúng
A.
\[{{({{3}^{a}})}^{b}}={{3}^{a+b}}\] B.
\[{{({{3}^{a}})}^{b}}={{3}^{a-b}}\] C. \[{{({{3}^{a}})}^{b}}={{3}^{ab}}\] D. \[{{({{3}^{a}})}^{b}}={{3}^{{{a}^{b}}}}\]
Đáp án:

A.
Hàm số lũy thừa
I.
Lý thuyết:
1.
Định nghĩa:
Là
hàm số có dạng \[y={{x}^{\alpha }}\] với \[\alpha \in R\]
2.
Tập xác định:
·
\[D=R\]với \[\alpha \] nguyên dương
·
\[D=R\backslash \left\{ 0 \right\}\]với
\[\alpha \]nguyên âm hoặc bằng 0
·
\[D=\left( 0;+\infty \right)\]với \[\alpha \]không nguyên
3.
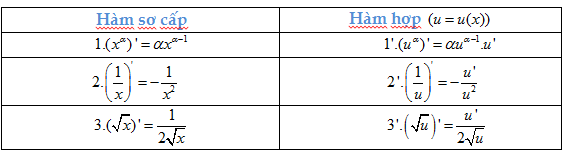
Đạo hàm:
Hàm số \[y={{x}^{\alpha }}\]( \[\alpha \in R\]) có đạo hàm với mọi x>0
1.
Tính chất của hàm số lũy thừa trên khoảng \[\left(
0;+\infty \right)\]:
·
Đồ thị
luôn đi qua điểm (1;1)
·
Khi \[\alpha >0\]hàm
số luôn đồng biến, khi \[\alpha <0\]hàm số luôn nghịch biến
·
Khi \[\alpha >0\]thì đồ thị hàm số
không có tiệm cận
·
Khi \[\alpha <0\]thì đồ thị hàm số
có tiệm cận ngang là Ox, tiệm cận đứng là Oy
II.
Ví dụ minh họa:
Câu 1: Tìm tập xác định D của hàm số \[y={{({{x}^{3}}-27)}^{\frac{\pi
}{2}}}\]
A. \[D=R\backslash \left\{ 2 \right\}\] B. \[D=R\]

Giải:
Lũy
thừa với cố mũ không nguyên thì cơ số dương
\[\to y={{({{x}^{3}}-27)}^{\frac{\pi
}{2}}}\] xác định khi \[{{x}^{3}}-27>0\Leftrightarrow x>3\]=> Chọn D
Câu 2: Tìm tập xác định D của hàm số \[y={{({{x}^{2}}-x-2)}^{-3}}\]
A. \[D=R\] B. \[D=R\backslash \left\{ -1;2 \right\}\]

Giải:
Lũy
thừa với số mũ nguyên âm thì cơ số phải khác 0
Hàm số đã cho xác định khi
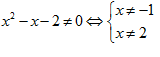
=> Chọn B
Câu 3: Tìm tập xác định D của hàm số \[{{\left[ {{x}^{2}}(x+1)
\right]}^{\sqrt{\pi }}}\]
A.
\[D=(0;+\infty )\] B. \[D=(-1;+\infty
)\backslash \left\{ 0 \right\}\] C. \[D=(-\infty ;+\infty )\] D. \[D=(-1;+\infty )\]
Giải:
Hàm số xác định khi
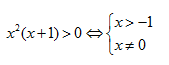
=> Chọn B
Câu 4: Hàm số \[y={{2}^{2{{x}^{2}}+x}}\]
có đạo hàm là
A. \[{{2}^{2{{x}^{2}}+x}}\ln 2\] B. \[(4x+1){{2}^{2{{x}^{2}}+x}}ln2\]
C. \[(2{{x}^{2}}+x){{2}^{2{{x}^{2}}+x}}ln2\] D. \[(4x+1){{2}^{2{{x}^{2}}+x}}ln2(2{{x}^{2}}+x)\]
Giải: \[y'=({{2}^{2{{x}^{2}}+x}})'={{2}^{2x2+x}}.\ln
2.(2{{x}^{2}}+x)'=(4x+1){{2}^{2{{x}^{2}}+x}}.ln2\]=>
Chọn B
Câu 5: Đạo hàm của hàm số \[y=2x+{{1}^{-\frac{1}{3}}}\]
trên tập xác định là
A.
\[2{{(2x+1)}^{-\frac{1}{3}}}\ln (2x+1)\] B. \[{{(2x+1)}^{-\frac{1}{3}}}\ln
(2x+1)\]
C. \[\frac{-2}{3}{{(2x+1)}^{-\frac{4}{3}}}\] D. \[\frac{-1}{3}{{(2x+1)}^{-\frac{4}{3}}}\]
Giải:
\[y'=\left[ {{\left( 2x+1 \right)}^{-\frac{1}{3}}}
\right]=-\frac{1}{3}(2x+1)'{{(2x+1)}^{-\frac{1}{3}-1}}=-\frac{2}{3}{{(2x+1)}^{-\frac{4}{3}}}\]=>
Chọn C
III.
Bài tập luyện tập:
Câu 1: Tìm tập xác định hàm số \[y={{(4{{x}^{2}}-1)}^{-4}}\]
A. \[R\backslash \left\{
\frac{-1}{2};\frac{1}{2} \right\}\] B. \[\left( \frac{-1}{2};\frac{1}{2}
\right)\] C. \[R\] D. \[(0;+\infty )\]
Câu 2: : Tìm tập xác định hàm số \[y={{(x+2)}^{\frac{\sqrt{2}}{3}}}\]
A. \[R\backslash \left\{ 2 \right\}\] B. \[(-2;+\infty )\] C. \[(0;+\infty )\] D. \[R\]
Câu 3:
Tìm tập xác định
hàm số \[y={{({{x}^{2}}-x)}^{-6cos\frac{\pi }{4}}}\]
A.
\[R\] B. \[R\backslash \left\{ 0;1 \right\}\] C. \[(0;1)\]
D. \[(-\infty
;0)\cup (1;+\infty )\]
Câu 4: Tìm đạo hàm của hàm số \[y={{({{x}^{2}}+1)}^{\frac{e}{2}}}\]trên
R
A.\[y'=2x{{({{x}^{2}}+1)}^{\frac{e}{2}-1}}\] B. \[y'=ex\sqrt{{{({{x}^{2}}+1)}^{e-2}}}\]
C. \[y'=\frac{e}{2}{{({{x}^{2}}+1)}^{\frac{e}{2}-1}}\] D. \[y'={{({{x}^{2}}+1)}^{\frac{e}{2}}}\ln
({{x}^{2}}+1)\]
Câu 5: Hàm số \[y={{(4{{x}^{2}}-1)}^{-4}}\]
có tập xác định là
A.
\[\left( \frac{-1}{2};\frac{1}{2} \right)\] B. R C. \[R\backslash \left\{
\frac{-1}{2};\frac{1}{2} \right\}\] D.\[(0;+\infty )\]
Câu 6: Hàm số \[y=\sqrt[5]{{{({{x}^{2}}+1)}^{2}}}\]
có đạo hàm là
A.
\[y'=\frac{4}{\sqrt[5]{{{({{x}^{2}}+1)}^{2}}}}\] B. \[y'=2x\sqrt{{{x}^{2}}+1}\]
C. \[y'=4x\sqrt[5]{{{x}^{2}}+1}\]
D. \[y'=\frac{4x}{5\sqrt[5]{{{({{x}^{2}}+1)}^{3}}}}\]
Câu 7: Tập xác định của hàm số \[y={{(2-3x)}^{\sqrt{5}}}\]
A.
\[D=R\backslash \left\{ \frac{2}{3} \right\}\] B. \[D=\left(
-\infty ;\frac{2}{3} \right)\]
C. \[D=\left( -\infty ;\frac{2}{3} \right]\] D.
\[D=\left( \frac{2}{3};+\infty \right)\]
Câu 8: Cho các hàm số \[{{f}_{1}}(x)=\sqrt{x},{{f}_{2}}(x)=\sqrt[4]{x},{{f}_{3}}(x)={{x}^{\frac{1}{3}}},{{f}_{4}}(x)={{x}^{\frac{1}{2}}}\].
Trong các hàm số trên, hàm số nào có tập xác định là nửa khoảng\[\left[
0;+\infty \right)\]
A.\[{{f}_{1}}(x),{{f}_{2}}(x)\] B. \[{{f}_{2}}(x),{{f}_{3}}(x)\] C. \[{{f}_{3}}(x),{{f}_{4}}(x)\] D.
\[{{f}_{2}}(x),{{f}_{3}}(x),{{f}_{4}}(x)\]
Câu 9: Đạo hàm của hàm số \[y=\frac{1}{{{2}^{x}}}\]
A. \[y'={{2}^{-x}}.\ln 2\] B. \[y'=\frac{-1}{{{2}^{x}}}\] C. \[y'=-\frac{\ln 2}{{{2}^{x}}}\] D. \[y'=-\frac{1}{{{({{2}^{x}})}^{2}}}\]
Câu 10: Hàm số \[y={{(4-{{x}^{2}})}^{\frac{3}{5}}}\]có
tập xác định là
A. R B.
\[(-\infty ;-2)\cup (2;+\infty )\] C. \[(-2;2)\]
D. \[R\backslash \left\{ \pm 2 \right\}\]
Đáp án:

CHÚC CÁC BẠN HỌC TỐT ^^







