
CHUYÊN ĐỀ: LOGARIT- HÀM SỐ
MŨ- HÀM SỐ LOGARIT
A.
Logarit:
I.
Lý thuyết:
1.
Định nghĩa:
a) a) Logarit cơ số a của b:
Cho
\[a,b>0;a\ne 1\]. Số
\[\alpha \]thỏa mãn đẳng thức \[{{a}^{\alpha }}=b\] được gọi là logarit
cơ số a của b và kí hiệu là \[{{\log
}_{a}}b\]:
Chú ý:
·
Không có logarit của số âm và số 0
·
Cơ số của logarit phải dương và khác 1
b) b) Logarit thập phân:
Logarit thập phân là logarit cơ số
10. Kí hiệu là \[\log b\]
c) c) Logarit tự nhiên:
Logarit
tự nhiên là logarit cơ số e. Kí hiệu là \[\ln b\]
Chú ý:
·
\[e=\underset{n\to
+\infty }{\mathop{\lim }}\,{{\left( 1+\frac{1}{n} \right)}^{n}}\]
2.
Tính chất:
Cho 2 số dương a, b và \[a\ne 1\], ta có các tính chất sau:

3.
Các
quy tắc tính logarit:
Cho
3 số dương a, b, c và \[a\ne 1\], ta có các quy tắc sau:

4.
Đổi
cơ số:
·
Cho 3
số dương a, b, c và \[a,c\ne 1\] , ta có
: \[{{\log }_{a}}b=\frac{{{\log }_{c}}b}{{{\log }_{c}}a}\]
·
Đặc biệt: \[{{\log
}_{a}}b=\frac{1}{{{\log }_{b}}a}(b\ne 1);lo{{g}_{{{a}^{\alpha
}}}}b=\frac{1}{\alpha }{{\log }_{a}}b(\alpha \ne 0)\]
II.
Ví dụ bài mẫu:
Câu 1:
tính giá trị của biểu thức \[P={{\log
}_{a}}(a.\sqrt[3]{a\sqrt{a}})(0
A. \[P=\frac{1}{3}\] B. \[P=\frac{3}{2}\] C. \[P=\frac{2}{3}\] D. \[P=3\]
Giải: \[P={{\log }_{a}}\left[ a.{{\left(
a.{{a}^{\frac{1}{2}}} \right)}^{\frac{1}{3}}} \right]={{\log }_{a}}\left(
{{a}^{\frac{3}{2}}} \right)=\frac{3}{2}{{\log }_{a}}a=\frac{3}{2}\]
ð Chọn
B
Câu 2:
cho a là số thực dương và khác 1. Tính giá trị
biểu thức \[P={{\log }_{\sqrt{a}}}a\]
A. \[P=-2\] B.
\[P=0\] C. \[P=\frac{1}{2}\] D. \[P=2\]
Giải: với \[0
ð Chọn
D
Câu 3:
cho a, b là các số thực dương khác 1 và thỏa
mãn \[ab\ne 1\]. Rút gọn biểu thức \[P=({{\log }_{a}}b+{{\log
}_{b}}a+2)({{\log }_{a}}b-{{\log }_{ab}}b){{\log }_{b}}a-1\]
A. \[P={{\log }_{b}}a\] B. \[P=1\] C. \[P=0\]
D. \[P={{\log }_{a}}b\]
Giải:
Từ giả thiết ta có :
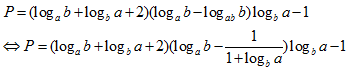
Đặt
\[t={{\log }_{b}}a\]
ð \[(t+\frac{1}{t}+2)(\frac{1}{t}-\frac{1}{1+t})t-1=\frac{{{\left(
t+1 \right)}^{2}}}{t}.\frac{1}{t(t+1)}t-1=\frac{t+1}{t}-1=\frac{1}{t}={{\log
}_{a}}b\]
ð Chọn D
Câu 4:
gọi a, b, c là các số thực khác 0 thỏa mãn \[{{4}^{a}}={{25}^{b}}={{10}^{c}}\].
Tính \[T=\frac{c}{a}+\frac{c}{b}\]
A. \[T=\frac{1}{2}\]
B. \[T=\sqrt{10}\] C. \[T=2\] D.
\[T=\frac{1}{10}\]
Giải:
giả sử
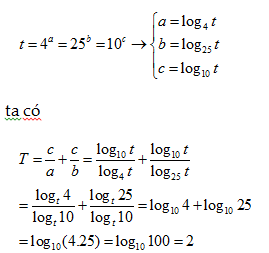
=>
chọn C
Câu 5:
đặt a=ln3, b=ln5. Tính \[I=\ln
\frac{3}{4}+\ln \frac{4}{5}+\ln \frac{5}{6}+...+\ln \frac{124}{125}\]theo
a và b
A.
\[I=a-2b\] B. \[I=a+3b\] C. \[I=a+2b\] D. \[I=a-3b\]
Giải: ta có
\[I=\ln
\left( \frac{3}{4}.\frac{4}{5}.\frac{5}{6}...\frac{124}{125} \right)=\ln
\frac{3}{125}=\ln 3-\ln 125=\ln 2-3\ln 5=a-3b\]
ð Chọn D
III.
Bài tập luyện tập:
Câu 1:
cho \[{{\log }_{2}}x=\sqrt{2}\]. Tính giá trị
biểu thức \[P={{\log }_{2}}{{x}^{2}}+{{\log }_{\frac{1}{2}}}{{x}^{3}}+{{\log
}_{4}}x\]
A.
\[P=\frac{11\sqrt{2}}{2}\] B. \[P=\sqrt{2}\] C. \[P=\frac{-\sqrt{2}}{2}\] D. \[P=3\sqrt{2}\]
Câu 2:
với a, b là các số thực dương tùy ý và a khác
1, đặt\[P={{\log }_{a}}{{b}^{3}}+{{\log }_{{{a}^{2}}}}{{b}^{6}}\] . Mệnh đề nào
dưới đây đúng?
A. \[P=27{{\log }_{a}}b\] B. \[P=15{{\log }_{a}}b\] C. \[P=9{{\log }_{a}}b\] D. \[P=6{{\log }_{a}}b\]
Câu 3:
cho \[a={{\log }_{2}}m\]
và\[A={{\log }_{m}}8m\] , với \[0
A. \[A=(3-a)a\] B. \[A=(3+a)a\] C. \[A=\frac{3-a}{a}\] D. \[A=\frac{3+a}{a}\]
Câu 4:
cho\[{{\log }_{2}}5=a,{{\log }_{3}}5=b\] .
Tính giá trị biểu thức\[A=\frac{{{\log }_{5}}120}{{{2}^{{{\log
}_{4}}\sqrt{2}}}}\] theo a và b
A.
\[A=\frac{2b+ab+a}{\sqrt[4]{2}ab}\] B. \[A=\frac{3b+ab+a}{ab}\] C. \[A=\frac{3b+ab+a}{\sqrt[4]{2}ab}\] D. \[A=\frac{b+ab+3a}{\sqrt[4]{2}ab}\]
Câu 5:
đặt \[a={{\log }_{2}}3\]và\[b={{\log
}_{5}}3\] . Hãy biểu diễn \[{{\log }_{6}}45\] theo a và b
A. \[{{\log
}_{6}}45=\frac{a+2ab}{ab}\]
B. \[{{\log
}_{6}}45=\frac{2{{a}^{2}}-2ab}{ab}\]
C. \[{{\log
}_{6}}45=\frac{a+2ab}{ab+b}\] D. \[{{\log }_{6}}45=\frac{2{{a}^{2}}-2ab}{ab+b}\]
Câu 6:
với mọi a, b, x là các số thực dương thỏa mãn
\[{{\log }_{2}}x=5{{\log }_{2}}a+3{{\log }_{2}}b\]. Mệnh đề nào dưới đấy đúng?
A. \[x=3a+5b\] B. \[x=5a+3b\] C.
\[x={{a}^{5}}+{{b}^{3}}\] D.
\[x={{a}^{5}}{{b}^{3}}\]
Câu 7:
cho a là số thực dương tùy ý khác 1. Mệnh đề
nào dưới đây đúng?
A. \[{{\log }_{2}}a={{\log
}_{a}}2\] B. \[{{\log
}_{2}}a=\frac{1}{{{\log }_{2}}a}\] C. \[{{\log }_{2}}a=\frac{1}{{{\log }_{a}}2}\] D.
\[{{\log }_{2}}a=-{{\log }_{a}}2\]
Câu 8:
với mọi số thực dương a va b thỏa mãn \[{{a}^{2}}+{{b}^{2}}=8ab\].
Mệnh đề nào dưới đây đúng?
A. \[\log (a+b)=\frac{1}{2}(\log
a+\operatorname{logb})\] B. \[\log (a+b)=1+\log
a+\operatorname{logb}\]
C.
\[\log (a+b)=\frac{1}{2}(1+\log a+\operatorname{logb})\] D. \[\log (a+b)=\frac{1}{2}+\log
a+\operatorname{logb}\]
Câu 9:
cho x, y là các số thực lớn hơn 1 thỏa mãn \[{{x}^{2}}+9{{y}^{2}}=6xy\].
Tính \[M=\frac{1+{{\log }_{12}}x+{{\log }_{12}}y}{2{{\log }_{12}}(x+3y)}\]
A. \[M=\frac{1}{2}\] B. \[M=1\] C. \[M=2\]
D. \[M=\frac{1}{3}\]
Câu 10:
cho các số thực\[a
A. \[\ln (ab)=lna+lnb\] B. \[\ln
{{({{a}^{2}}-b)}^{3}}=3\ln ({{a}^{2}}-b)\]
C. \[\ln \left( \frac{a}{b} \right)=\ln |a|-\ln |b|\] D. \[\ln {{\left(
\frac{a}{b}
\right)}^{2}}={{\operatorname{lna}}^{2}}-{{\operatorname{lnb}}^{2}}\]
Đáp án:

A.
Hàm số mũ-hàm số
logarit
I.
Lý thuyết hàm số mũ:
1.
Định nghĩa: Hàm số có dạng \[y={{a}^{x}}(0
2.
Tập xác định:\[D=R\],
tập giá trị \[(0;+\infty )\]
3.
Đạo hàm:
Hàm số \[y={{a}^{x}}(0
4.
Sự biến thiên:
·
Khi \[a>1\]:
hàm số đồng biến
·
Khi \[0
5.
Đồ thị: đồ thị hàm số có tiệm cận ngang là trục Ox và luôn đi qua
các điểm \[(0;1),(1;a)\]và nằm về phía trên trục hoành
II.
Lý thuyết hàm số logarit:
1.
Định nghĩa: hàm số có dạng \[y={{\log }_{a}}x(0
2.
Tập xác định: \[D=(0;+\infty )\],
tập giá trị R
3.
Đạo hàm: hàm số \[y={{\log }_{a}}x(0
4.
Sự biến thiên:
·
Khi \[a>1\]
: hàm số đồng biến
·
Khi \[0
5.
Đồ thị: đồ thị hàm số có tiệm cận ngang là trục Oy và luôn đi qua
các điểm \[(1;0),(a;1)\]và nằm về phía
phải trục tung
Nhận xét: đồ thị hàm số \[y={{a}^{x}}\]và
đồ thị hàm số \[y={{\log }_{a}}x\] đối xứng với nhau qua đường thẳng \[y=x\]
III.
Ví dụ bài mẫu:
Câu 1:
Tìm tập xác định D của hàm số \[y={{\log
}_{2}}({{x}^{2}}-2x-3)\]
A.
\[D=(-\infty ;-1]\cup [3;+\infty )\] B. \[D=[-1;3]\]
C. \[D=(-\infty ;-1)\cup (3;+\infty )\] D. \[D=(-1;3)\]
Giải: Hàm số xác định
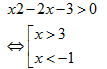
Vậy tập xác định của
hàm số là \[D=(-\infty ;-1)\cup (3;+\infty )\]
ð Chọn
C
Câu 2:
tìm tập xác định D của hàm số \[y={{\log
}_{2}}\frac{x-1}{x}\]
A. \[D=(0;1)\] B. \[D=(1;+\infty
)\] C. \[D=R\backslash \left\{ 0
\right\}\] D.
\[D=(-\infty ;0)\cup (1;+\infty )\]
Giải: Hàm số xác định:
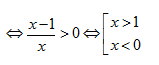
ð Chọn
D
Câu 3:
tìm tập xác định D của hàm số \[y=\sqrt{{{\log
}_{2}}(x+1)-1}\]
A. \[D=(-\infty ;1]\] B. \[D=(3;+\infty )\] C. \[D=[1;+\infty )\] D. \[D=R\backslash \left\{ 3
\right\}\]
Giải: hàm số xác định:
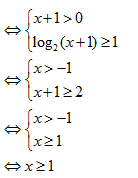
ð Chọn
C
Câu 4:
tính đạo hàm của hàm số \[y={{(2{{x}^{2}}+x-1)}^{\frac{2}{3}}}\]
A.
\[y'=\frac{2(4x+1)}{3\sqrt[3]{2{{x}^{2}}+x-1}}\] B. \[y'=\frac{2(4x+1)}{3\sqrt[3]{{{(2{{x}^{2}}+x-1)}^{2}}}}\]
C. \[y'=\frac{2(4x+1)}{2\sqrt[3]{2{{x}^{2}}+x-1}}\] D. \[y'=\frac{2(4x+1)}{2\sqrt[3]{{{(2{{x}^{2}}+x-1)}^{2}}}}\]
Giải: \[y={{(2{{x}^{2}}+x-1)}^{\frac{2}{3}}}\]
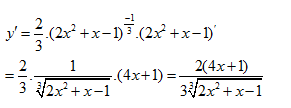
ð Chọn A
Câu 5:
tính đạo hàm của hàm số \[y={{13}^{x}}\]
A.
\[y'=x{{.13}^{x-1}}\] B. \[y'={{13}^{x}}.\ln 13\] C. \[y'={{13}^{x}}\] D. \[y'=\frac{{{13}^{x}}}{\ln
13}\]
Giải: \[y'=({{13}^{x}})'={{13}^{x}}.\ln 13\]
ð Chọn
B
Câu 6:
tính đạo hàm của hàm số \[y=f(x)={{x}^{\pi }}.{{\pi }^{x}}\]tại điểm x=1
A. \[f'(1)=\pi \] B.
\[f'(1)={{\pi }^{2}}+\ln \pi \]
C. \[f'(1)={{\pi }^{2}}+\pi \ln \pi \] D. \[f'(1)=1\]
Giải: đạo hàm
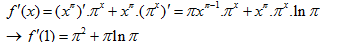
ð Chọn
C
Câu 7:
hàm số nào sau đây đồng biến trên khoảng \[(0;+\infty
)\]
A. \[y={{\log
}_{\frac{\sqrt{2}}{2}}}x\] \[\] B. \[y={{\log }_{\frac{e}{2}}}x\] C. \[y={{\log
}_{\frac{e}{2}}}x\]
D. \[y={{\log }_{\frac{e}{4}}}x\]
Giải:
Áp dụng lý thuyết:
Hàm số \[y={{\log
}_{a}}x\]đồng biến khi \[a>1\], nghịch biến khi \[0<>
Trong các hàm số đã
cho chỉ có hàm số \[y={{\log }_{\frac{e}{2}}}x\]đồng biến vì cơ số \[a=\frac{e}{2}>1\]
ð Chọn
C
Câu 8:
tìm tất cả các giá trị của tham số a để hàm số
\[y={{({{a}^{2}}-3a+3)}^{x}}\]đồng biến
A. \[a=1\] B. \[a=2\] C. \[a\in (1;2)\] D. \[a\in (-\infty ;1)\cup
(2;+\infty )\]
Giải: hàm số đồng biến khi
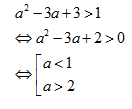
ð Chọn
D
Câu 9: đường cong trong hình dưới là đồ thị của 1 hàm số trong 4 hàm số được liệt kê ở 4 phương án A, B, C, D dưới đây. Hàm hàm số đó là hàm số nào?
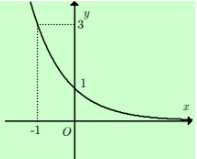
A. \[y={{(\sqrt{3})}^{x}}\]
B. \[y={{\left( \frac{1}{2}
\right)}^{x}}\] C. \[y={{2}^{x}}+\frac{5}{2}\] D. \[y={{\left( \frac{1}{3}
\right)}^{x}}\]
Giải:
Dựa vào hình dáng đồ thị từ trái sang phải ta thấy x tăng nhưng
y giảm
ð Hàm số tương ứng của đồ thị là hàm nghịch biến.
Loại A, C
Đồ thị hàm số đi qua điểm có tọa độ (-1;3) nên chỉ có D
thỏa mãn
ð Chọn
D
Câu 10: đường cong trong hình dưới là đồ thị của 1 hàm số trong 4 hàm số được liệt kê ở 4 phương án A, B, C, D dưới đây. Hàm hàm số đó là hàm số nào?
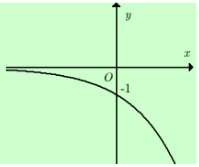
A. \[y=-{{2}^{x}}\] B.
\[y={{\left( \frac{1}{2} \right)}^{x}}\] C. \[y={{2}^{x}}\] D.
\[y=-{{\left( \frac{1}{2} \right)}^{x}}\]
Giải:
Đồ thị nằm phía dưới trục hoành. Loại B, C
Lấy đối xứng đồ thị qua trục hoành ta được đồ thị của một
hàm số đồng biến
ð Chọn
A
IV.
Bài tập luyện tập:
Câu 1:
tìm tập xác định D của hàm số \[y=\ln \left(
|x-5|+5-x \right)\]
A. \[D=R\backslash \left\{ 5
\right\}\] B. \[D=(-\infty ;5)\] C. \[D=(5;+\infty )\] D.
\[D=R\]
Câu 2:
Tìm tất cả các già trị thực của tham số m để
hàm số \[y=\ln ({{x}^{2}}-2mx+m)\]có tập xác định là R
A. \[m<0;m>1\] B. \[0
Câu 3:
hàm số nào dưới đây có tập xác định là đoạn \[[-1;3]\]?
A. \[y=\ln (3+2x-{{x}^{2}})\] B. \[y=\frac{1}{3+2x-{{x}^{2}}}\] C. \[y=\sqrt{3+2x-{{x}^{2}}}\] D.
\[y=\frac{1}{\sqrt{3+2x-{{x}^{2}}}}\]
Câu 4:
cho a là số thực dương khác 1. Tìm điề kiện của
x để \[x={{\log }_{a}}{{a}^{x}}\]xảy ra
A. \[\forall x\] B.
\[x>0\] C.
\[x\ge 0\] D.
\[x>1\]
Câu 5:
cho hàm số \[y=f(x)={{2}^{x}}{{.5}^{x}}\].
Tính \[f'(0)\]
A. \[f'(0)=10\] B. \[f'(0)=1\] C. \[f'(0)=\frac{1}{\ln 10}\] D. \[f'(0)=ln10\]
Câu 6:
cho hàm số \[f(x)=5{{e}^{{{x}^{2}}}}\].
Tính \[P=f'(x)-2x.f(x)+\frac{1}{5}.f(0)-f'(0)\]
A.
P=1 B. P=2 C. P=3 D. P=4
Câu 7:
cho hàm số \[f(x)={{2}^{{{x}^{2}}}}+1\].
Tính \[T={{2}^{-{{x}^{2}}-1}}.f'(x)-2x\ln 2+2\]
A.T=-2 B. T=2 C. T=3 D.T=1
Câu 8:
tìm tất cả các giá trị thực của tham số a để
hàm số \[y={{\log }_{M}}x\] với \[M={{a}^{2}}-4\] nghịch biến
trên tập xác định
A. \[2<>
B. \[a=\sqrt{5}\] C. \[-\sqrt{5}<>
Câu 9:
cho a, b là 2 số thực thỏa mãn \[{{a}^{\frac{\sqrt{3}}{3}}}>{{a}^{\frac{\sqrt{2}}{2}}}\]và
\[{{\log }_{b}}\frac{3}{4}<{{\log }_{b}}\frac{4}{5}\]. Mệnh đề nào sau đây
đúng?
A. \[0<><>
B. \[0
Câu 10:
cho hàm số\[y=x-\ln (1+x)\]. Khẳng định nào
sau đây đúng?
A.
Hàm
số giảm trên \[(-1;+\infty )\]
B.
Hàm
số tăng trên \[(-1;+\infty )\]
C.
Hàm
số giàm trên \[(-1;0)\] và tăng trên \[(0;+\infty )\]
D.
Hàm
số tăng trên \[(-1;0)\]và giảm trên \[(0;+\infty
)\]
Câu 11:
cho a là 1 số thực dương khác 1 và các mệnh đề
sau:
1) \[{{a}^{x}}>0\]
với mọi \[x\in R\]
2) Hàm số \[y={{a}^{x}}\]đồng biến trên R
3) Hàm số \[y={{e}^{2017x}}\]
là hàm số đồng biến trên R
4) Đồ thị hàm số \[y={{a}^{x}}\]
nhận trục Ox làm tiệm cận ngang
Hỏi có bao nhiêu mệnh đề đúng?
A. 1 B. 2 C.
3 D.4
Câu 12: cho a, b, c là các số thực dương khác 1. Hình vẽ dưới là đồ thị của ba hàm số \[y={{a}^{x}},y={{b}^{x}},y={{c}^{x}}\]. Khẳng định nào sau đây đúng?
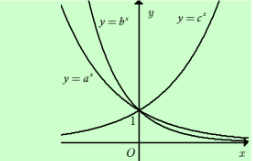
A. \[a>b>c\] B. \[a<>
Câu 13:
cho hàm số \[y={{5}^{x}}\]có
đồ thị (C ) . Hàm số nào số đây có đồ thị đối xứng với © qua đường thẳng y=x
A.
\[y={{5}^{-x}}\] B.
\[y={{\log }_{5}}x\] C. \[y=-{{\log
}_{5}}x\] D.
\[y=-{{5}^{-x}}\]
Câu 14:
cho hàm số \[y={{3}^{\frac{x}{2}}}\] có đồ thị (C ) . Hàm số nào số đây có đồ thị đối
xứng với ( C) qua đường thẳng y=x
A. \[y={{\log }_{\sqrt{3}}}x\] B.
\[y={{\log }_{3}}{{x}^{2}}\] C. \[y={{\log }_{3}}\frac{x}{2}\] D. \[y=\frac{1}{2}{{\log
}_{3}}x\]
Câu 15:
cho \[{{9}^{x}}+{{9}^{-x}}=23\]. tính giá trị
biểu thức \[P=\frac{5+{{3}^{x}}+{{3}^{-x}}}{1-{{3}^{x}}-{{3}^{-x}}}\]
A. \[P=2\] B. \[P=1\] C. \[P=3\] D. \[P=\frac{-5}{2}\]
Đáp án:








