Các dạng bài toán thực tế chuyên đề Hàm mũ – Hàm logarit
I. Bài toán lãi suất :
1. Lãi đơn :
Số tiền lãi chỉ tính trên số tiền gốc mà không tính trên số tiền lãi do số tiền gốc sinh ra.
Công thức tính lãi đơn:
\[T=M(1+r.n)\]
Trong đó: T: Số tiền cả vốn lẫn lãi sau n kỳ hạn;
M: Tiền gửi ban đầu;
n: Số kỳ hạn tính lãi;
r: Lãi suất định kỳ, tính theo %
Ví dụ 1 : Anh T gửi vào ngân hang thương mại và phát triển một số tiền là 10.000.000đ với lãi đơn là 6%/năm . Hỏi sau 10 năm anh T nhận lại số tiền là bao nhiêu ?
Giải
Cách 1 : Cứ 1 năm anh T lại nhận được số tiền lãi là 10.000.000 x 6% = 600.000(đ)
\[\Rightarrow \]Như vậy sau 10 năm anh T nhận được số tiền lãi là 600.000đ x 10 = 6.000.000đ và 10.000.000đ tiền gốc .Như vậy anh T nhận được số tiền là 16.000.000.
Cách 2 : Ta có : T=10000000.(1+10.6%)
-> T=16000000
Như vậy sau 10 năm tổng số tiền anh T nhận lại là 16.000.000đ
2. Lãi kép :
Là số tiền lãi không chỉ tính trên số tiền gốc mà còn tính trên số tiền lãi do tiền gốc đó
sinh ra thay đổi theo từng định kỳ .
v Lãi kép gửi một lần rồi đi rút tiền : \[T=M{{(1+r)}^{n}}\]
Trong đó: T: Số tiền cả vốn lẫn lãi sau n kỳ hạn;
M: Tiền gửi ban đầu;
n: Số kỳ hạn tính lãi;
r: Lãi suất định kỳ, tính theo %
Ví dụ 2 : ( Đề minh họa 2018 ) Một người gửi 100 triệu đồng vào một ngân hàng với lãi suất 0,4%/tháng .Biết rằng nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi tháng , số tiền lãi sẽ được nhập vào vốn ban đầu để tính lãi cho tháng tiếp theo . Hỏi sau đúng 6 tháng , người đó được lĩnh số tiền (cả vốn ban đầu và lãi ) gần nhất với số tiền nào dưới đây , nếu trong khoảng thời gian này người đó không rút tiền ra và lãi suất không thay đổi ?
A.102.424.000 đồng B.102.423.000 đồng
C.102.016.000 đồng D.102.017.000 đồng
Giải
Từ công thức : \[T=M{{(1+r)}^{n}}\]
Ta có M=100.000.000 đồng , r=0,4% và n =6 tháng
\[\Rightarrow T=M{{(1+r)}^{n}}\]
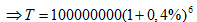
\[\Rightarrow T=102424128\approx 102424000\]đồng
v Lãi kép gửi định kỳ :
· Tiền được gửi vào cuối mỗi tháng : \[T=\frac{M}{r}\left[ {{\left( 1+r \right)}^{n}}-1 \right]\]
· Tiền được gửi vào đầu mỗi tháng : \[T=\frac{M}{r}\left[ {{\left( 1+r \right)}^{n}}-1 \right]\left( 1+r \right)\]
Ví dụ 3 : Một người gửi hàng tháng vào ngân hàng số tiền là 100 USD . Biết lãi suất hàng tháng là 0,35% . Hỏi sau một năm người đó có bao nhiêu tiền ?( Lấy giá trị gần nhất )
A.1 000 USD B. 1100 USD
C. 1200 USD D. 1300 USD
Giải
Từ công thức : \[T=\frac{M}{r}\left[ {{\left( 1+r \right)}^{n}}-1 \right]\left( 1+r \right)\]
Ta có M = 100 USD , r = 0,35% , n=12 tháng
\[\Rightarrow T=\frac{M}{r}\left[ {{\left( 1+r \right)}^{n}}-1 \right]\left( 1+r \right)\]
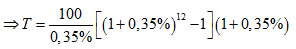
\[\Rightarrow T\approx 1227\,\text{USD}\]
Vậy sau 1 năm số tiền người đó có là 1227 USD -> Đáp án C
Ví dụ 4 : Mỗi tháng gửi tiết kiệm 580.000đ với lãi suất 8,4% / năm . Hỏi sau 15 tháng thì lãnh về cả vốn lẫn lãi là bao nhiêu ?
A.9 triệu B. 10 triệu 200K
C. 9 triệu 130K D. 10 triệu 230K
Giải
Từ công thức : \[T=\frac{M}{r}\left[ {{\left( 1+r \right)}^{n}}-1 \right]\]
Ta có M = 580.000đ , r= 0,7% , n=15 tháng
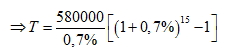
\[\Rightarrow T=9139505\,\]đồng -> Đáp án C
3. Bài toán trả góp :
Là hình thức mua hàng mà ở đó người mua không cần phải trả toàn bộ số tiền trong một lần trả, mà có thể thanh toán nó theo kỳ hạn .
\[P{{(1+r)}^{n}}=\frac{M}{r}\left[ {{\left( 1+r \right)}^{n}}-1 \right]\]
Ví dụ 5 : Anh A mua nhà giá trị 300 triệu đồng theo phương thức trả góp
a, Nếu cuối tháng bắt đầu từ tháng thứ nhất anh A trả 5500000đ và chịu lãi suất số tiền chưa trả là 0,5%/tháng thì sau bao nhiêu lâu anh A trả hết số tiền :
A. n=64
B. n=60
C. n=65
D. n=63
Giải
Từ công thức : \[P{{(1+r)}^{n}}=\frac{M}{r}\left[ {{\left( 1+r \right)}^{n}}-1 \right]\]
Ta có : P = 300tr , M = 5,5tr ,r = 0,5%
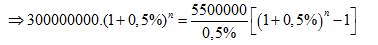
\[\Rightarrow n=64\]
b, Nếu anh A muốn trả hết nợ trong vòng 5 năm và phải trả lãi với mức 0,5%/năm thì mỗi tháng anh A phải trả bao nhiêu tiền ( làm tròn đến nghìn đồng )
A. 5035000đ
B. 5000000đ
C. 5064000đ
D. 5030000đ
Giải
Từ công thức : \[P{{(1+r)}^{n}}=\frac{M}{r}\left[ {{\left( 1+r \right)}^{n}}-1 \right]\]
Ta có P=300tr , r = 0,04167% , n = 60
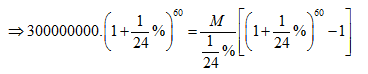
\[\Rightarrow M=5063800\]đ
II. Bài toán tăng trưởng :
Ø Ta có công thức : \[S=A.{{e}^{n.i}}\]
Trong đó A : là dân số của năm được lấy làm mốc
S : Là dân số sau n năm
i : là tỉ lê tăng dân số hàng năm .
Ví dụ 6 : Dân số Việt Nam năm 2017 là 90 triệu dân . Tăng trưởng dân số hàng năm là 1,32% . Dân số sau 10 năm của Việt nam là bao nhiêu ?
A. 102,7
B. 102,6
C. 109,55
D. 107,85
Giải
Từ công thức : \[S=A.{{e}^{n.i}}\]
Ta có : A=90 triệu , n = 10 năm , \[i\]= 1.32 %
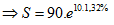
\[\Rightarrow S=\,\,102,699\]triệu
III. Bài toán về sự phân rã phóng xạ :
Ø Ta có công thức : \[{{m}_{\left( t \right)}}\,=\,{{m}_{\left( 0 \right)}}.{{\left( \frac{1}{2} \right)}^{\frac{t}{T}}}\]
Trong đó : \[{{m}_{\left( 0 \right)}}\]: là khối lượng chất phóng xạ ban đầu
\[{{m}_{\left( t \right)}}\] : là khối lượng chất phóng xạ tại thời điểm t
T : là chu kì bán rã
Ví dụ 7 :Chu kỳ bán ra của chất phóng xạ Pu là 24360 năm ( tức là sau 24360 năm phân hủy thì chỉ còn lại một nửa ) . Hỏi 10g Pu sau bao nhiêu năm phân hủy sẽ còn lại 1g ?
A. 80922,17 năm
B. 80933,17 năm
C. 80233,17 năm
D. 81933,17 năm
Giải
Từ công thức : \[{{m}_{\left( t \right)}}\,=\,{{m}_{\left( 0 \right)}}.{{\left( \frac{1}{2} \right)}^{\frac{t}{T}}}\]
Ta có : \[{{m}_{\left( t \right)}}\] = 1g , \[{{m}_{\left( 0 \right)}}\]=10g , T = 24360 năm
\[\Rightarrow 1=10.{{\left( \frac{1}{2} \right)}^{\frac{t}{24360}}}\]\[\Rightarrow \,\frac{1}{10}={{\left( \frac{1}{2} \right)}^{\frac{t}{24360}}}\]\[\Rightarrow \,{{\log }_{\frac{1}{2}}}\frac{1}{10}=\frac{t}{24360}\]\[\Rightarrow \,t=80922,17\]năm
IV. Một số bài tập tự luyện :
Câu 1 : Muốn có 100 triệu đồng sau 10 tháng thì phải gửi tiết kiệm mỗi tháng là bao nhiêu mỗi tháng với lãi suất gửi là 0,6% .
A. 9 triệu
B. 9 triệu 3
C. 9 triệu 7
D. 10 triệu
Câu 2 : Một người gửi 6 triệu vào ngân hàng theo hình thức lãi kép , kì hạn 1 năm với lãi suất 7,56% / năm . Hỏi sau bao nhiêu năm ngừoi gửi sẽ có 12 triệu từ số tiền gửi ban đầu ?
A. 9,511
B. 10,511
C. 11,511
D. 12,511
Câu 3 : Đem 100 triệu đi gửi ngân hàng với lãi suất 8%/năm thì sau 2 năm có bao nhiêu tiền ?
A. 118,35
B. 116,64
C. 119,55
D. 127,85
Câu 4 : Số lượng vi khuẩn ban đầu là 100 con và sau 5 giờ thành 300 con. Hỏi sau 10 giờ có bao nhiêu con vi khuẩn ?
A.800 B. 900 C. 1000 D. 1100
Câu 5 : Rn là chất phóng xạ có chu kì bán rã T = 3,8 ngày. Khối lượng Rn lúc đầu \[{{m}_{\left( 0 \right)}}\] = 2g. Khối lượng rađôn còn lại sau 19 ngày là bao nhiêu?
A. 0,0625g B. 1,9375g C. 1,2415g D. 0,7324g
Câu 6 : Cho chu kỳ bán rã của Pôlôni T = 138 ngày. Giả sử khối lượng ban đầu \[{{m}_{\left( 0 \right)}}\] = 1g. Hỏi sau bao lâu khối lượng Pôlôni chỉ còn 0,707g?
A. 69 ngày B.138 ngày C. 276 ngày D. 18 ngày
Câu 7 : Urani U có chu kì bán rã là \[4,{{5.10}^{9}}\]năm. Giả sử rằng tuổi của Trái Đất là \[{{5.10}^{9}}\] năm. Hãy tính lượng còn lại của 1g U kể từ khi Trái Đất hình thành.
A. 0,463 g B. 0,2 g C. 0,4 g D. 0,25 g
Câu 8 : Bạn A cầm 58 triệu đem gửi tiết kiệm ở ngân hàng với lãi suất 0,7%/tháng . Hỏi 8 tháng sau ra rút tiền thì ngân hàng phải trả bạn A bao nhiêu tiền ?
A. 64 triệu
B. 60 triệu
C. 61 triệu
D. 65 triệu
Câu 9 : Biết rằng tỷ lệ giảm dân số hàng năm ở Nga là 0,5%. Năm 1998 , dân số Nga là 146.861.000 người . Hỏi vào năm 2008 dân số Nga sẽ là bao nhiêu ?
A. 141 triệu người
B. 143 triệu người
C. 152 triệu người
D. 150 triệu người
Câu 10 : Cho một lượng vi khuẩn ban đầu là 500 con phát triển với vận tốc tỉ lệ với số lượng . Biết sau 3 giờ , có 8000 con . Hỏi sau 4 giờ số lượng vi khuẩn là bao nhiêu ?
A. 46352 con
B. 40235 con
C. 20159 con
D. 32259 con
Đáp án








